- 作者/李政憲
對應課程:八年級「勾股定理」、九年級「相似形」、「生活中的立體圖形」
需要材料:A4或B4影印紙
為什麼影印紙要設計成這個長寬比例?
- 你知道生活中常用的影印紙的長寬比例是多少嗎?
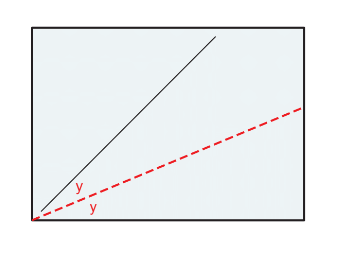
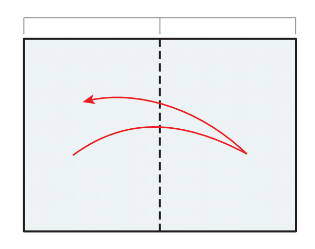
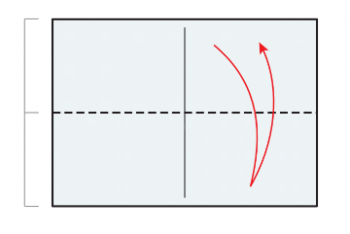
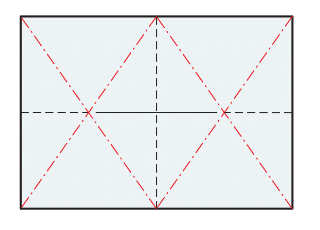
請拿起一張影印紙(A4 或 B4 皆可),依照圖 1 和圖 2 的方式摺摺看,就會發現在圖 1 中摺出來的等腰直角三角形的斜邊(圖中虛線),和影印紙的長邊竟然是相等的。
而又由於影印紙的短邊就是等腰直角三角形的一股長,假設短邊長為 1,等腰直角三角形的斜邊長就會是\(\sqrt{2}\),又斜邊與長邊等長,因此影印紙的長邊與短邊的長度比就是 \(\sqrt{2}\):1 了。

- 至於影印紙為什麼要設計成 \(\sqrt{2}\):1 這個比例呢?
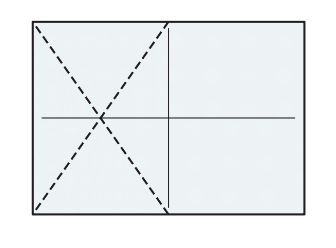
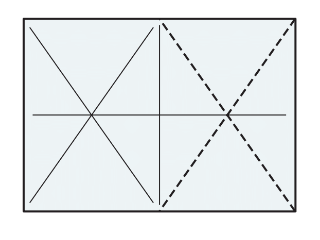
其實有個很重要的原因。請不妨再拿一張相同大小的影印紙,對半裁切後將其中一半旋轉 90 度,再與另一張完整影印紙的左上方兩邊對齊,你會發現兩張長方形的對角線恰可連成一直線(如圖 3~4),也就是兩個長方形彼此是相似的(因為兩多邊形相似的條件為:對應角相等,且對應邊成比例)。
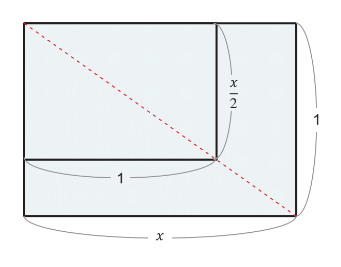
若我們假設原紙張的短邊為 1,長邊為 x,則我們可以列出 x:1=1:\(\frac{x}{2}\)的算式,故 \(x^{2}\)=2,便可得出 x=\(\sqrt{2}\) 的結果。
也就是若我們將影印紙沿長邊中點連線對半裁切(或將大小相等的兩張影印紙以長邊拼合)得到的紙張,將與原影印紙的比例相同。
如此一來,若我們影印時需要縮小圖形,就只需要將原影印紙作長邊對半裁切,則縮小的影印紙與原影印紙的大小比例相同,原作品大小與影印出來的結果也會彼此相似,放大時也是同樣的道理。
而透過影印紙的巧妙比例,我們可以製作出一些十分有趣的作品。讓我們先從一個簡單的四角錐開始做起吧!
用影印紙做出四角錐
首先請拿一張影印紙, 如圖 5、6 分別在長短邊各摺出其中點連線後,再摺出長邊中點與原矩形的四個端點的連線,如圖 7、8。
李老師小聲說:「如果想節省空間與紙張,讀者也可將 A4 尺寸的影印紙,應用其 \(\sqrt{2}\):1 的特性,將其裁切為等比例的兩等份或四等份,再進行後續的摺製與組裝。」
接下來如圖 9,將最後摺製的四條連線由谷線改為山線,且左右兩交叉點的連線不摺(圖中實線處),即可依山谷線分佈完成如圖 10 的四角錐。

由於這個作品目前無法定型,建議可以翻至背面,將內縮突起的直角三角形,分別摺製其兩銳角的角平分線(如圖 11、12),即可將圖 10 放於平面時作簡單固定如圖 13,而若要固定得更完整,也可以口紅膠或膠水將中間的鈍角三角形接合面黏貼,就不會有容易移動的情形了。



接下來按照上面方式摺製共六個四角錐,並用膠帶將其對應邊接合如圖 14,即可將六個四角錐翻摺形成一個正立方體如圖 15,且此六個角錐的頂點恰重合於正立方體的中心處。
李老師小聲說:「事實上,圖 14 是其中一種正方體展開圖的組合方式,各位不妨試試與圖 14 不同的其他組合方式,也是很有趣的哦!」


不曉得各位有沒有覺得很神奇呢?我們以幾張生活中隨手可得的影印紙,幾道簡單的摺痕,就可以完成一個正立方體,這也代表每個角錐恰是正方體體積的六分之一!這是為什麼呢?
- 為了討論這個問題,我們不妨看一下圖 16。
若將正方體從中心點與八個頂點連線,可將此正方體切割為六個角錐,假設這個正方體的邊長為 1,則可計算出其底部正方形的對角線為 \(\sqrt{2}\),再根據勾股定理,可以算得此正方體最遠的兩頂點間的距離為 \(\sqrt{3}\),也就是此四角錐的稜長為 \(\frac{\sqrt{3}}{2}\) 。
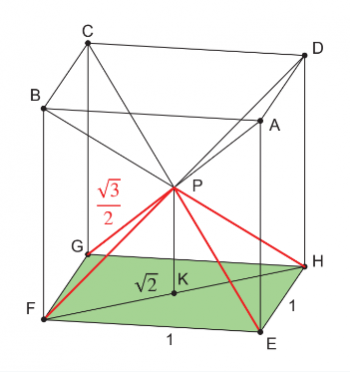
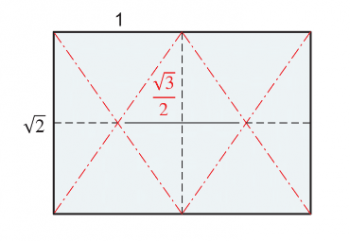
接下來我們再看圖 17 的四角錐展開圖,根據剛剛摺製的過程,長邊的一半即為正方體的邊長=1,應用影印紙的比例,我們可以得知短邊長為 \(\sqrt{2}\),故其稜長(即長邊中點與四個端點連線段長的一半)為 \(\frac{\sqrt{3}}{2}\),也就是說這麼摺製出來的四角錐就和上面從正方體切割出的角錐稜長相等、底面積也相等囉!
李老師小聲說:「亦可考慮以平行線截等比例線段,求得角錐的高度為正方體邊長的一半來說明。」
——本文摘自泛科學 2019 年 10 月選書《藝數摺學》,2019 年 9 月,臉譜出版。