到目前為止,吠陀立方系列文章已經介紹過流傳千年的古印度數學-吠陀方形(Vedic square),我運用數字感把它加上一個維度定義了吠陀立方(Vedic cube),再以樓層法去解析位數根胚騰(Digital root patterns)層層之間的關係[1],這回來介紹吠陀立方對稱面法。
吠陀立方:將吠陀方形從平面延伸成立體
吠陀方形就是將大家熟悉的九九乘法表中每一個數字進行位數根(digital root)運算,例如說 4 乘上 8 會得到 32,把 3 加上 2 得到 5,這個 5 即為 32 的位數根,也是吠陀方形裡座標點(4, 8)的數值。吠陀方形在西元 770 年被穆斯林納入伊斯蘭文化的數學知識體系之中[2]。
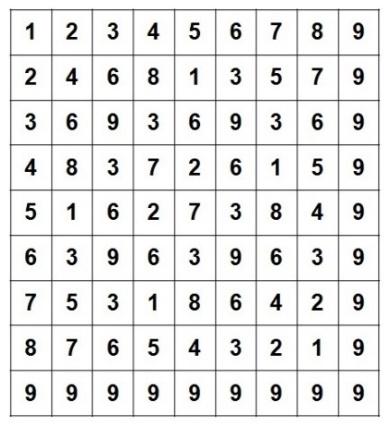
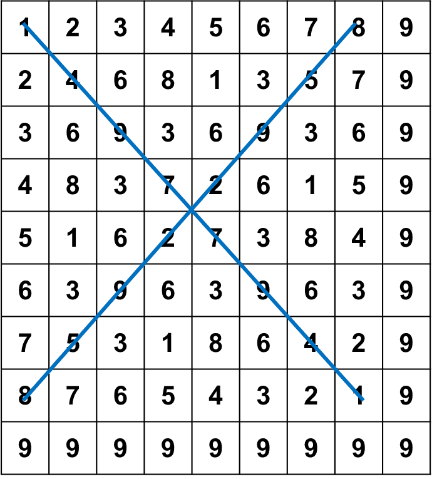
其中位數根所在的位置互相連結後組成的胚騰(pattern)構成了特定的幾何圖案如下圖:

吠陀立方則是將吠陀方形從平面延伸成立體,也就是三個數字相乘的三維乘法表(9×9×9),是整個立方體中各個座標點的數字進行位數根運算後的結果,可以用函數 D(X, Y, Z) 代表吠陀立方中座標 (X, Y, Z) 該數字的位數根,實際運算時的數學式為 D(X×Y×Z)。例如座標點 (2, 4, 7)在吠陀立方中的數值即為 D(2×4×7) = D(56) = D(11) = D(2) = 2。
之前提到以程式繪出吠陀立方中的位數根胚騰,其散布情況相當複雜(可見此篇),難以看出這些座標點在空間中構成的意義。用樓層法解析吠陀立方,能夠觀察出位數根胚騰在各層本身的性質,甚至可從二維的吠陀方形推算不同樓層之間的變換。只是樓層法是把三維空間轉化成許多二維平面,較少探討位數根胚騰在三維空間中彼此的相關性,這時又該如何是好呢?
解構吠陀立方
回到數學或科學研究的基本方法,觀察、觀察、再觀察。
吠陀方形中,位數根 1 至位數根 8 位置構成的八個圖樣會沿著兩條對角線 X=Y 與 X+Y=9 對稱,兩條對角線為對稱軸,不僅在 X-Y 平面可以成立,在 Y-Z 平面、X-Z 平面同樣成立。從二維拓展至三維的過程中,對角線就變成了對角面同時也是對稱面,因此吠陀立方共有六個對稱面。
為了找到空間中最小不可分割的塊體,也就是不重複的基本元素(element),以及內部對應的座標點,希望能探討位數根胚騰在三維空間中的關係,所以我將沿著對稱面群切割與解構吠陀立方。
吠陀立方的對稱面群分為兩組,一組叫做主對稱面群(main symmetry planes, MSP),為 X=Y, Y=Z, X=Z,這三個對稱面都有通過原點,如圖 4;另一組則為副對稱面群(secondary symmetry planes, SSP),為 X+Y=9, Y+Z=9, X+Z=9,如圖 5。
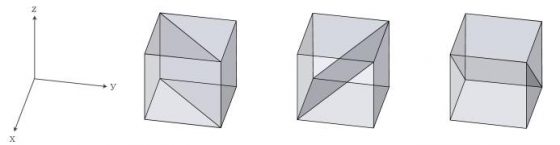
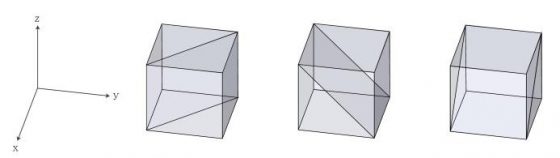
圖 4 和圖 5 的每一塊灰色塊體,都可藉由一次鏡射後得到完整的吠陀立方。至於分析的塊體取對稱面群兩邊任何一塊皆可,並沒有限制要取對稱面群的哪一邊。除此之外,可以選擇先在 X-Y, Y-Z, X-Z 平面沿著主副對稱面群切割,得到的塊體將是三角柱體,其底面為 1/4 正方形面積的等腰直角三角形。
沿著主對稱面群分割吠陀立方的結果如圖 6,得到 6 個 MSP 四面體(MSP unit tetrahedron),值得注意的是這 6 個四面體為雙直角四面體(birectangular tetrahedron),顧名思義此四面體包含兩個直角,在數學上也稱為 Schläfli orthoscheme。此雙直角四面體的底面為 1/2 正方形面積的等腰直角三角形,高為立方體的邊長,因此體積為吠陀立方的1/6。
每一個 MSP 四面體可沿著 X=Y, Y=Z, X=Z 共鏡射三次得到吠陀立方。主對稱面群的交集為一條線,也就是吠陀立方的對角線 X=Y=Z,因此會將吠陀立方分成 6 塊。
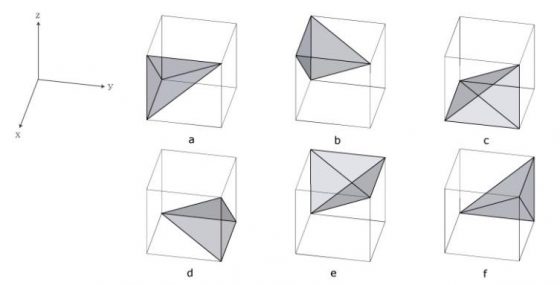
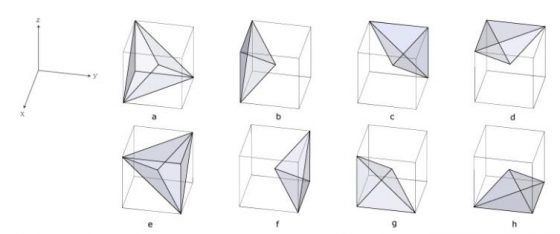
副對稱面群分割後的結果為 8 個塊體如圖 7,包括 2 個 SSP 六面體(SSP unit hexahedron),體積各佔吠陀立方的 1/4;以及 6 個 SSP 四面體(SSP unit tetrahedron),其底面為 1/2 正方形面積的等腰直角三角形,高為吠陀立方邊長的 1/2,體積各佔吠陀立方的 1/12。副對稱面群的交集為一個點,為吠陀立方的中心 (4.5, 4.5, 4.5),因此會將立方體分成 8 塊,而這 8 塊的體積並不完全相同。
把幾何問題從書桌搬到餐桌!

在思考副對稱面群分割問題時,為了驗證自己的想法,在愛爾蘭的聖誕假期,我把所有的研究材料從書桌搬到了餐桌,以做菜來輔助研究,餓的話馬上補充體力。
平常雖然沒有那麼喜歡豆腐,但豆腐不僅好切、還能增進空間幾何的思考,更可以照顧到五臟廟,在廚房實作數學效果意外倍增!老實說,這麼可愛的幾何豆腐還真讓人有點捨不得吃掉呢。

切完豆腐和著其他食材煮湯飽食一頓以後,問題也快解完了。最後的步驟是沿著另一個對稱面群繼續分割,即使副對稱面群分割出的塊體並不全然相同,但最終結果為一單位四面體,其底面為 1/4 正方形面積的等腰直角三角形,高為立方體邊長的 1/2,體積各佔吠陀立方的 1/24,如圖 9。
原先主對稱面群分割的 MSP 四面體(1/6 立方體體積)會被副對稱面群的邊界條件分為形狀相等的 4 小塊;而副對稱面群分割出的塊體則有二種情況,第一種為 SSP 六面體(1/4 立方體體積)將會被主對稱面群的邊界條件分為形狀相等的 6 小塊,第二種情況則是 SSP 四面體(1/12 立方體體積)將被分為形狀相等的 2 小塊。
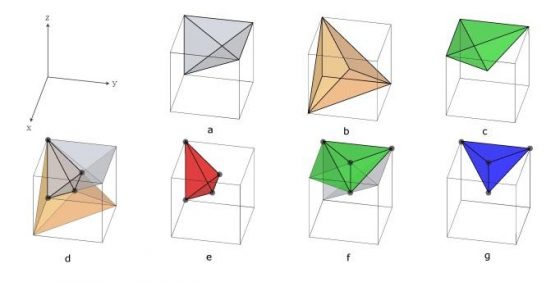
無論由主對稱面群或是從副對稱面群開始分割,得到的結果相同,為 24 塊全等的四面體如圖 10,稱之為吠陀立方單位四面體(unit tetrahedron of Vedic cube, UTVC),為三直角四面體(trirectangular tetrahedron),表示其中一個頂角包含三個直角。任一個 UTVC 已是最小不重複的基本元素,可沿著對稱面群鏡射六次得到原先的吠陀立方。

也就是說,我們只要列出 UTVC 裡面的位數根 1、2、3、4 座標點位(可藉由旋轉分別得到位數根 8、7、6、5,如吠陀方形的位數根胚騰),就可以將原先複雜的座標點位分布,簡化成不能再簡化的胚騰。
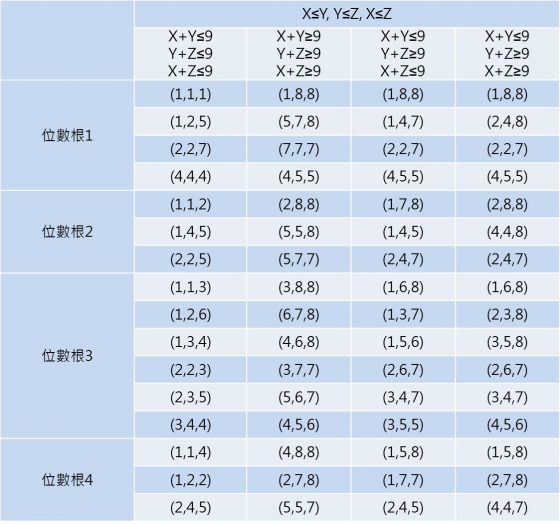
表1列出了位數根 1、2、3、4 在 4 個 UTVC 中的座標點位。表中的點包含了邊界條件上的點,這些點會被數個 UTVC 同時共用。UTVC 中的位數根座標點沿著對稱面群確實能鏡射出其他位數根座標點,而每個 UTVC 中座標點構成的向量也相同。
- 表1|位數根 1、2、3、4 在 4 個 UTVC 中的座標點。
從二維平面至三維空間,吠陀立方的更多應用
吠陀立方的發展是從二維平面至三維空間,其簡化是了解三維空間的位數根胚騰性質的重要步驟。從對稱面群解構的方法可大幅簡化吠陀立方的複雜度,也可找出三維空間的基本元素,不再限於吠陀方形於二維平面隱含的圖樣與規律(樓層法)。
位數根於吠陀立方散布的胚騰,是大自然本身形成的奧妙形態,除了純數學研究或是建構演算規則外,也許能和分子晶體、空間、藝術或是建築等相關領域結合應用。像是行為藝術教母瑪莉娜·阿布拉莫維奇(Marina Abramović)與她的夥伴曾在Nightsea Crossing的作品中,根據吠陀方形而決定各自所穿的衣服顏色。

吠陀立方是受到古印度數學吠陀方形、伊斯蘭幾何圖樣、倫敦蛇形藝廊 2002 的啟發,跨越數千年與東西方文化最終在台灣這個文化交融之地產生的數學。我身為吠陀立方的發明與發現者,特別期待未來有人能受到啟發,將吠陀立方的概念運用於建築設計或藝術創作,就像是塞西爾.巴爾蒙德(Cecil Balmond)運用演算法把正方形轉化成蛇形藝廊 2002 那樣令人驚艷。
對我來說,數學與藝術是兩面鏡子,可以一直相互映射彼此的光亮;而東方和西方,也能夠不斷跨越邊界彼此對話與啟發。
後續,我們再來聊聊如何將吠陀立方轉化成數學藝術創作。
參考資料
- Lin, C. Y. Digital Root Patterns of Three-Dimensional Space. Recreational Mathematics Magazine, 3(5), 9–31, 2016.
- Jones, L. “Mathematics and Islamic art”, Mathematics in School, 18(4), 32–35, 1989.