行政院長林全宣布暫緩開放日本核災地區食品進口,這是繼 2009 年美國牛肉進口爭議之後,政府的食安科學在民眾的疑慮之中敗下陣來。

2008 年韓國民眾才為美牛問題進行大規模示威抗議不久,馬英九政府在美方壓力之下也簽署了「美國牛肉輸台議定書」,引起民眾一片譁然。政府希望能說服民眾的理由,是吃美國牛肉得狂牛病因而致命的機會極小。當時美國在臺協會台北辦事處處長司徒文說沒有人吃美國牛肉致死,而台灣在 2008 年有一千多人騎機車死亡,「沒有人說騎機車不安全」。衛生署長葉金川也附和說吃美牛得狂牛病的機會跟被雷打到兩次一樣,「是非常低的風險」。
機會、命運,請選擇
2010 年,我隨台灣旅美政治學者訪問團回台,有機會面見當時的行政院吳敦義院長及馬英九總統,談到美牛進口爭議。我建言說用「機率」來為食安政策辯護是無法說服民眾的。我說:政府發行公益彩券,其中獎機率幾乎為零,難道政府要勸民眾放棄中獎的希望?而即使中獎機率極小是科學的客觀事實,這對民眾也沒有說服力,因為民眾買彩劵,相信的是「命運」而不是「機會」。
以大樂透為例:大樂透每注中頭獎的機率只有 1/13,980,000,而每期有高達數百萬注的銷售量。如果下注的買家都如政府在食安議題上所希望的、從客觀頻率的觀點來詮釋機率並以之作為行為的依據,他們就不會下注了,而公益彩券恐怕也早就破產了!事實是:下注的民眾在開獎前都還是抱著會中獎的希望,而如果這還不夠,很多人會燒香拜佛禱告,希望神明保佑他們中獎。

政府在食安問題上用低風險來遊說民眾之所以沒有效果,是因為官員們不知道民眾對機率的認知是跟他們完全不一樣的。從風險管理上來看,不論是公益彩劵或食安管控,政府完全可以用客觀頻率的概念來計算機率、期望值。以大樂透而言,如果每期賣出 5 百萬注,則可以算出最少有一注中頭獎的機率是 0.30;政府可以和賭場一樣很精確地預期盈虧。同樣的道理,在食安的問題上,政府也可以估計大約會有幾人得病或死亡。如果這個數目甚低,政府覺得可以容忍,便據以制定食品進口政策。這個決策過程可以是科學的,但它的客觀性恰恰造成與民眾認知的差距。
對於民眾而言,他們買彩劵在乎的不是全部共有幾人得獎,而是自己有沒有得獎。在食安問題上,他們擔心的不是一共有幾人致病,而是他們自己或家人、親友會不會致病。
即使客觀上致病的機率不大,但主觀上相信下注大樂透有中獎可能的民眾,自然不會排除不幸命運降臨的可能性。對民眾而言,食安問題正是所謂「黑天鵝」事件:它的機率雖小,危害卻極大。
「如果不覺得騎機車不安全,便沒有理由說吃美牛不安全」,這是錯誤的命題。首先,民眾對交通安全並不是完全放心。他們即使出門不見得會燒香禱告,也可能在身上、車上放平安符。而一般人在親友出遠門時,總會致上旅途平安的祝福,正是反映了對交通安全的顧慮。他們了解,意外事故是有可能降臨自身的,只是現代生活不能沒有交通,不能因咽廢食罷了。說不怕車禍便沒有理由怕美牛或核災食品,難道要民眾在上餐廳時攜帶平安符或在餐桌上互相祝禱 “Have a safe meal”?而且,在交通問題上,民眾期待的是政府能夠從基本建設上減少車禍的機率,而開放有食安顧慮的食品進口卻是增加致病的機率,這當然不符合民眾對政府的期待。
主觀機率、客觀機率,大大不同
即使撇開命運不談,民眾對於美牛或核災地區食品風險的估計,也會與政府的科學估計有所不同。政府官員從風險管理的立場出發,自然要收集科學證據與統計資料,盡量客觀地估計食安問題對民眾健康造成危害的機率。但是一般人對於機率的認知,卻通常帶有主觀的成分。
這種傾向,在 1970 年代即為心理學家、2002 年諾貝爾經濟學獎得主康尼曼(Daniel Kahneman)與其早逝的合作者特沃斯基(Amos Tversky)所發現。康尼曼與特沃斯基的理論主張一般人在作風險決策時,沒有能力用科學、客觀的方法估計機率,而是用一些簡單、有效率的捷徑來作為主觀估計的依據。這些捷徑,他們稱之為 heuristics,意思是具啟發性的簡便法則。
康尼曼與特沃斯基的研究歸納出三種主要法則:
記憶所及簡法(availability heuristic):以記憶所及的相關事件來估計機率
代表性簡法(representativeness heuristic):根據事件的代表性來估計機率
定點調整簡法(anchoring and adjustment heuristic):以一個數目為基底,然後往上或往下調整估計
根據這些簡法估計出來的機率通常會偏離客觀機率,造成估計誤差。記憶所及的事件常受媒體或個人經驗影響;具代表性特質的事件當然不見得發生次數就高;而作為基底的數目即使是隨機決定的,也常會影響到調整後的估計。
舉例而言,六個兒女的家庭,其性別出生序一共有 2 x 2 x 2 x 2 x 2 x 2 = 64 種可能的排列法。因為每一胎生男生女的機率各為 0.5,而且各胎是男是女都是互相獨立的事件,這 64 種出生序都是同樣可能的。可是當康尼曼與特沃斯基在實驗中問受測者「女男女男男女」和「男女男男男男」哪一種出生序可能性較高時,超過 80% 的受測者認為第一種出生序較為可能。即使是比較各有三男三女的「女男男女男女」和「男男男女女女」,大多數人仍然認為第一種排序的可能較高。康尼曼與特沃斯基舉此實驗為「代表性簡法」造成估計偏差的例證,因為一般人都認為上述兩組的第二種排序較無代表性。
另一個例子:下列兩個陳述中,你認為哪個的可能性較高?
林教授自 2010 年以來,諸事不順。
林教授自 2010 年與馬英九總統握手以來,諸事不順。

如果你認為第二個陳述的可能性較高,可能你是受到「記憶所及簡法」的影響了,因為記憶中有某某人與馬總統握手過就倒楣的媒體報導;你如果相信它,記憶所及,就容易想像,感覺上可能性就高。但是在邏輯上,第一個陳述包含第二個,因此其可能性較高。
以食安問題而言,當人們記憶所及是媒體對狂牛病或核災感染食品危害健康的報導時,他們對食安風險的估計會使用「記憶所及簡法」,因而造成高估的偏差。(筆者長期住在美國,吃牛肉毫無顧忌。記憶中,從未看到美國媒體對這議題有所報導。)
其實,康尼曼與特沃斯基後來發展成型的「前景理論」(prospect theory)就直接主張一般人會高估客觀上較低的機率而低估客觀上較高的機率。像大樂透中頭獎或吃美牛得狂牛病這種客觀上接近於 0 的機率,在小數點之後有那麼多 0,一般人是沒法想像的。多幾個 0 或少幾個 0 對民眾而言其實是無感,可是當他們看到報導有人中頭獎或得狂牛病,他們對這些機率的主觀估計就不會是 0,而會比 0 顯著地高。
當人們主觀上認為吃美牛或核災地區食品有得病致死的可能時,他們對進口有安全疑慮食品的期望值就會比現狀糟糕了,當然無法接受政府開放進口的政策。這一點,應用康尼曼與特沃斯基的前景理論,我們還可以從民眾的立場做更進一步的風險決策分析。
前景理論的風險決策分析
前景理論的風險決策分析與傳統理論不同之處,在於後者在計算預期效益時用客觀機率來加權價值,而前者則用主觀機率。除了對主觀機率的假設外,前景理論對價值(或效益)函數也做了一些特殊的假設。如果用 π(.) 代表主觀機率作為客觀機率的函數、v(.) 代表價值作為「得」、「失」結果的函數,前景理論的主要假設可以簡單敘述如下:
機率函數
- 客觀機率為 0 的結果其主觀機率亦為 0:π(0)=0。
- 客觀機率為 1 的結果其主觀機率亦為 1:π(1)=1。
- 客觀機率甚小的結果,其主觀機率大於客觀機率:若 p 甚小,則 π(p) > p。
- 客觀機率較大的結果,其主觀機率小於客觀機率:若 p 甚小,則 π(1-p) < 1-p。
- 較大客觀機率在主觀上被低估的幅度,可能大於甚小客觀機率在主觀上被高估的程度:若 p 甚小,則 (1-p) – π(1-p) ≥ π(p)-p,也就是 π(p) + π(1-p) ≤ 1。
- 其它與本文無直接關係的假設。
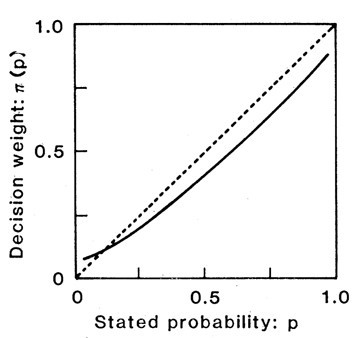
下圖是康尼曼與特沃斯基所假設的加權函數,也就是主觀機率函數。
價值函數
- 無「得」無「失」的結果其價值為 0:v(0)=0。
- 有所「得」的正面的結果,其價值函數往正向呈現邊際效益遞減的趨勢。
- 有所「失」的負面的結果,其價值函數往負向呈現邊際效益遞減的趨勢。
- 相對於同樣數量的「得」,「失」所造成的傷害程度大於「得」所帶來的滿足程度:若 x<0,則 |v(x)|>|v(-x)|。
- 風險決策的預期價值為「得」、「失」結果價值用主觀機率加權後的總和:若風險決策得到 x 結果的客觀機率為 p,得到 y 結果的客觀機率為 q,則風險決策的預期價值為 V(x,p;y,q) = π(p)v(x) + π(q)v(y),此預期價值也稱作「前景」(prospect)。
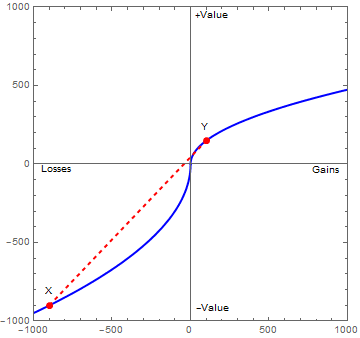
下圖中的藍色曲線是康尼曼與特沃斯基價值函數的一個例子。曲線上的紅點代表兩個結果 x 與 y,其價值分別為 v(x)=-900 與 v(y)=150。紅色虛線代表兩個價值以所有可能之主觀機率加權後之總和,也就是預期價值。π(p) 越大則預期價值越靠近 x 點 ;π(q) 越大則預期價值越靠近 y 點。
我們現在可以用前景理論來分析一般民眾在決定要不要支持政府開放進口有安全疑慮食品的政策了。這個決定包含兩個選項:支持開放進口或維持不進口的現狀。因為支持開放會有兩個可能結果:(x)因食用不安全的食品而致病、(y)得到更多的安全食品,而民眾做決定時並不能確定哪一種結果會發生,只能主觀估計這些結果的機率,所以他們的決定是一種風險決策。我們可以把選項的各種可能結果更清楚地表示如下:
A. 不支持開放進口,其結果為 s。這個結果是確定的也就是客觀機率為 1。若不支持開放進口並不會改變現狀,則我們可以假設現狀的價值為 v(s)=0 。因為此結果的客觀機率為 1 ,其主觀機率 π(1)=1。選項 A 的前景為 0。
B. 支持開放進口,其結果為 x 的客觀機率為 p、為 y 的客觀機率為 q。選項 B 的前景為兩種結果用主觀機率加權後的預期價值 V(x,p;y,q) = π(p)v(x) + π(q)v(y)。
前景理論雖然認為民眾在估計機率時會有主觀、甚至不理性的情形,然而在主觀機率形成之後,他們做決定的邏輯卻仍然與理性選擇一樣,也就是用預期價值(前景)的相對大小來決定選項。在這裡,只有當
V(x,p;y,q) = π(p)v(x) + π(q)v(y) > 0
成立的時候,民眾才會選擇 B,也就是支持政府開放進口的政策。以上圖為例,這代表 x 與 y 的預期價值必須要在紅色虛線在橫軸之上的那一部分,民眾才會願意承擔風險。
上式中,如果 v(x) 與 v(y) 均為正值,不等式是一定成立的,民眾會支持開放;如果 v(x) 與 v(y) 均為負值,不等式則一定不成立,民眾不支持開放。但這裡 v(x)<0 而 v(y)>0,所以不等式是否成立要進一步分析。政府官員決策的依據,是用科學研究的結論認定食安有問題的機率極小,也就是 π(p) = p→0,如此則 V(x,p;y,q) = π(q)v(y) > 0,不等式亦成立,民眾應該可以放心政府的開放政策,甚至還可以享受食品多樣性的正面價值。
這種一廂情願的想法,卻不能讓民眾接受,那是因為民眾做決定時用的不是傳統經濟學的理性選擇邏輯,而是認知心理學前景理論的邏輯。上面說過,前景理論不因為 p 甚小就認為 π(p) = p→0 而是認為 π(p) >p,也就是民眾不認為食安問題的負面結果可以完全忽略:風險選項的預期價值必須要把 π(p)v(x) 納入考量。
上面作為民眾買單的不等式可以轉換為
-v(x) < [π(q)/π(p)] v(y)
注意,這裡 -v(x) 是因食用不安全進口食品所造成的傷害(負值)的負值;因為負負得正,我們可以用 |v(x)| 來代替它。將它代入上式得
|v(x)| < [π(q)/π(p)] v(y)
這個不等式是否成立?為了方便討論,我們且根據前景理論的假設做一些數值估計。因為 p 甚小,民眾主觀上會高估它,我們假設 π(p) = 0.01(百分之一)是個合理的估計。再者,因為 p+q=1,所以 q = 1-p = 0.99 是個甚大的機率,它會被低估,而且它被低估的程度會大於 p 被高估的程度。我們假設 π(q)=0.90。將 π(p)=0.01 與 π(q)=0.90 代入上式得
|v(x)| < 90v(y) 或 |v(x)|/v(y) < 90
也就是說,只有那些主觀上認為健康的代價小於美國牛肉或核災地區食品所能帶來的滿足感的 90 倍的民眾,才會願意甘冒風險支持政府的進口政策!只要健康的代價相對於食品滿足感足夠大,儘管致病的客觀機率甚小,因為主觀上其可能性不可忽略,民眾不會支持政府。注意:這裡因為致病是「失」而滿足感是「得」,根據前景理論,即使失與得同額,民眾在價值估計上對失去健康的反應也會更強烈的。
也許您認為上面的數值假設太不合理,那讓我們修改一下。現在假設要開放的食品會致病的主觀機率是π(p)=0.001(千分之一),而 π(q)=0.990,則
|v(x)| < 990v(y)
讀者們可以自問您健康的代價會小於美國牛肉或核災地區食品所能帶給您的滿足感的 990 倍嗎?如果您的答案是肯定的,您就可以放心支持政府開放進口的政策了。
政府要如何才能說服民眾支持開放進口?
前景理論最為人所熟知的結果,恐怕是它能用來預測人們對待風險的態度。一般來說,因為價值函數的邊際效益遞減,一般人在面對「得」的情況比較會想要避免風險(risk-averse),而在面對「失」的情況比較願意承擔風險(risk-acceptant)。這其實不是鐵律,真正的風險態度還是要從比較選項的預期價值來決定。

從馬政府到蔡政府,不論是進口美牛或核災地區食品,最令民眾困惑的是為何在有食安疑慮的情況下,政府仍然那麼亟於開放進口這些食品。雖然媒體猜測政府背後有來自美、日、或世貿組織的壓力,但政府從未曾把不開放進口的後果明確讓民眾知道,因此民眾在做風險決策時,並未嚴肅考慮不支持開放進口的後果。
如果民眾清楚知道不開放的的負面後果,那他們是不是就會比較願意承擔風險而支持開放進口?要回答這個問題,我們必須將上面的分析略作修正。此時選項 A 的結果 s 的價值不再為 0,而是 v(s)<0,其主觀機率仍然是 π(1)=1。選項 A 的前景為 v(s)<0。因此,民眾願意支持開放進口、承擔風險的條件是:
V(x,p;y,q) = π(p)v(x) + π(q)v(y) > v(s)
因為 v(s)<0,很顯然這個條件會比較容易達到,但我們還可以進一步把它轉換成:
|v(x)| < [π(q)/π(p)] v(y) + [1/π(p)] |v(s)|
這裡不等式右邊第一項根以前一樣,第二項的 |v(s)|=-v(s) 是不開放進口的後果的絕對值,這可以包括受到美、日、甚至 WTO 反制的代價。若我們如前假設 π(p)=0.01 與 π(q)=0.90,則
|v(x)| < 90v(y) + 100 |v(s)|
相信有不少民眾會同意:台灣受到重要國際友邦和組織反制的代價,比起美國牛肉或核災地區食品所能帶給個人的滿足感要高出太多了,何況有安全疑慮的食品即使進口,個人也可以不吃。在這種考量下,應該會有更多民眾願意承擔風險、支持政府的政策。
政府官員必須了解:當你們以巨額獎金引誘民眾下注公益彩券的時候,你們不能夠同時要求他們不要擔心有安全疑慮的進口食品;當你們用科學方法從事食安風險管理的時候,你們不能夠簡單地認為幾個人死亡和幾個人中獎一樣,是在政府治理可以容許的範圍之內,而冀求民眾支持。
本文嘗試說明:民眾不但相信命運甚於相信機會、系統性高估微小機率,對負面結果的反應也較正面結果更強烈。在進口有安全疑慮食品這個議題上,日、韓政府、馬政府都已嚐過苦頭,蔡政府不應該不汲取教訓。真的有國際關係上不得不然的苦衷,應該實話實說,民眾自然會加以考慮。科學是冷酷的,政府不能不尊重科學,但更不能不尊重民眾的思考方式和安全考量。
本文〈為何科學無法克服民眾的食安疑慮?〉轉載自 Tse-min Lin 的部落格。