如果貝氏定理的哲學基礎豐富得出人意料，那定理的數學則是單純得令人震驚。定理最基本的形式只是一組代數表達式，有三個已知的變項，一個未知的變項。但這個單純的公式可以導出非常有預測力的洞見。
貝氏定理與條件機率（conditional probability）有關。也就是說，這個定理會告訴我們如果某些事件發生之後，某個理論或假設為真的機率有多少。
假設你跟一位伴侶同居，你出差回來的時候，發現你衣櫃的抽屜裡有件陌生的內衣。你或許會問自己：你的伴侶出軌的機率有多少？條件是你發現了內衣；你有興趣評估的假設是你被背叛的機率有多少。信不信由你，貝氏定理就能給你這類問題的答案—前提是你知道（或願意評估）三個數量：
- 首先，你必須以內衣的出現作為假設為真—也就是說，你被背叛了—的條件，評估這樣的機率是多少。為了處理這個問題，讓我們假設你是女性，而你的伴侶是男性，我們討論中的內衣是一件內褲。如果他背叛了你，當然很容易想像內褲是怎麼來的。反之，就算（而且或許尤其是）他真的背叛了你，你或許也會希望他更小心一點。我們假設以他背叛你為條件，內褲出現的機率是百分之五十。
- 第二，你必須以內衣出現作為假設為偽的條件。如果他沒有不忠，那內褲的出現有沒有什麼合理的解釋？當然，不是所有的解釋都能讓人滿意（那可能是他的內褲）。可能是他的行李被搞亂了。可能是他一位純友誼的女性朋友，是你也信任的人，來過了夜。內褲可能是要給你的禮物，他忘了包起來。這些理論沒有一個是完全站不住腳的，不過有些跟「狗把我的作業吃掉了」這樣的藉口差不多。整體來說，你給這些理論的機率放在百分之五。
- 第三，也是最重要的，你需要貝氏學派所說的「先驗機率」（prior probability，或單純稱為先驗，prior）。你在找到內衣之前，你認為他背叛你的機率有多高？當然，既然內褲已經出現了，對這點就很難完全客觀了。（理想上來說，你在開始檢視證據之前就要建立你的先驗機率了。）但有時候是有可能從經驗上來評估像這樣的數字的。例如，研究發現在特定的任何一年，大約有百分之四已婚的伴侶會對配偶不忠，所以我們就以這個為我們的先驗機率。
如果我們估計過這些數值，那麼就可以運用貝氏定理來建立後驗機率（posterior possibility）。這就是我們有興趣的數字：根據我們找到的內衣，我們被背叛的機率有多高？計算結果（以及產生結果的單純代數表達式）。
先驗機率：
他背叛你的可能性初始估計：x = 4%
新事件發生：找到神秘內衣
以他背叛為條件，出現內衣的機率：y = 50%
以他沒有背叛為條件，出現內衣的機率：z = 5%
後驗機率：
已知你找到內衣，修正後他背叛你的可能估計：xy / [xy + z ( 1 – x )] = 29%
結果發現這個機率還是相當低：百分之二十九。這樣似乎還是違反直覺—這些內衣不就很能顯示他有罪了嗎？但是這個數字主要來自於你指派給他背叛的先驗機率很低。雖然無辜的男人不像有罪的男人那樣，對出現內褲有那麼多花言巧語的解釋，但是你一開始就認為他是個無辜的男人，所以在等式裡就佔了很大的比重。
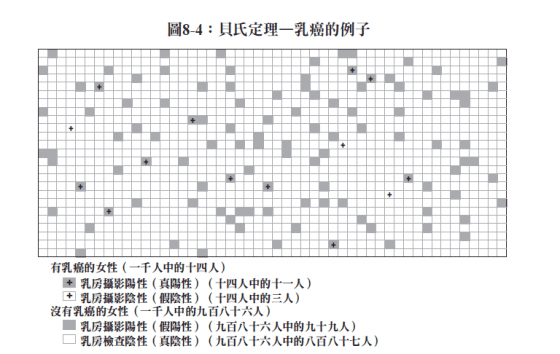
先驗機率高的時候，儘管有新證據出現，還是會強韌得令人訝異。這個狀況典型的例子之一就是四十多歲的女性出現乳癌的狀況。女性在四十多歲時得到乳癌的機會很幸運的相當低—大約百分之一‧四。但是如果乳房攝影檢查結果是陽性，那機率又是多少？
研究顯示，如果女性沒有罹患癌症，而乳房攝影錯誤斷言說她有癌症的機率大約只有百分之十。另一方面，如果她確實有癌症，有百分之七十五的機會會偵測出來。你看到這些統計數字的時候，陽性的乳房攝影結果似乎的確是非常糟糕的消息。但要是你把貝氏定理用到這些數字上，你就會得到不同的結論：假定四十歲的女性乳房攝影為陽性，她得乳癌的機率還是只有大約百分之十。這些假陽性的結果會比這個等式看起來地位更高，是因為年輕女性本來就很少會有乳癌。因為這個理由，所以許多醫生建議，女性要到五十歲以後再開始做定期乳房攝影，那時得乳癌的先驗機率要高得多。
像這樣的問題無疑挑戰極大。最近有份研究，用調查來了解美國民眾對統計的認識程度，就讓民眾看了這個乳癌的例子，發現只有百分之三的民眾提出的機率估計是正確的。有時候，慢下腳步用視覺看看問題（如圖8-4），可以檢查我們不正確的趨近法是否合乎事實。這樣的方式讓人比較容易看到更大的層面—由於乳癌在年輕女性身上非常稀少，所以陽性的乳房攝影結果這件事並不是那麼有效。
然而，我們通常會專注在最新、最直接可得的資訊，而看不到更大的層面。像鮑勃‧伏加瑞斯這樣的聰明賭徒已經學會如何利用我們思考的這種缺陷。他下注湖人隊大有賺頭，一部分是因為莊家太過看重湖人隊的前面幾場比賽，把他們贏得冠軍的機率從四分之一降到六‧五分之一，即使以一支有位明星球員受傷的球隊來說，他們這樣的表現已經算不錯了。貝氏定理需要我們更謹慎地去考量這些問題，在我們憑感覺得到的趨近法實在太過於粗糙的時候，可以靠這個定理來檢測，它非常有用。
然而，這不表示我們的先驗機率永遠都比新證據地位更高。或是說貝氏定理本來就會產出違反直覺的結果。有時候新的證據非常有力，可以推倒其他一切，而某件事我們可以從原來指派近乎零的機率，立刻就改為幾乎必然發生。
想一想這個令人難過的例子：九一一恐怖攻擊。那天早上起床的時候，我們多數人幾乎都不會指派任何機率給恐怖分子用飛機撞進曼哈頓的大樓這樣的事件。但是第一架飛機一撞上世界貿易中心，我們就承認了恐怖攻擊是種明顯的可能。第二棟大樓一被撞上，我們被攻擊這件事就無庸置疑了。貝氏定理可以複製這個結果。
例如，假設在第一架飛機撞上之前，我們估計曼哈頓的高樓遭受恐怖攻擊的可能性只有大約兩萬分之一，或是百分之○‧○○五。然而，我們指派給飛機因為意外而撞上世界貿易中心的機率也非常低。這些數字是真的可以用經驗估計出來的：九一一事件之前的兩萬五千天之中，曼哈頓上空的航空狀況出現過兩次這樣的意外，一次是一九四五年的帝國大廈，另一次是一九四六年在華爾街四十號。這樣在任何特定的一天，這種意外發生的機率就是一萬兩千五百分之一。如果你用貝氏定理來運算這些數，第一架飛機撞上的那一刻，我們分派給恐怖攻擊的機率就會從百分之○‧○○五增加到百分之三十八。
然而，貝氏定理背後的概念不是要我們只要更新一次機率的估計就好。而是說，隨著我們看到新的證據出現，我們就應該不斷地這樣做。因此，在第一架飛機撞上之後，我們恐怖攻擊的後驗機率：百分之三十八，在第二架飛機撞上之前，就變成了我們的先驗機率。而要是你再次計算這個算式，來考慮第二架飛機撞上世貿中心的狀況，那我們遭受攻擊的機率就變成了幾乎確定—百分之九十九‧九九。
先驗機率：
恐怖份子會用飛機撞上曼哈頓的摩天大樓，其可能性的初始估計：x = 0.005%
新事件發生：第一架飛機撞上世貿中心
如果恐怖份子攻擊曼哈頓的摩天大樓，飛機撞上的機率：y = 100%
恐怖分子沒有攻擊曼哈頓的摩天大樓，飛機撞上的機率：z = 0.008%
後驗機率：
已知第一架飛機撞上世貿中心，對恐怖攻擊修正後的機率估計：xy / [xy + z ( 1 – x )] = 38%
先驗機率：
已知第一架飛機撞上世貿中心，對恐怖攻擊修正後的機率估計：x = 38%
新事件發生：第二架飛機撞上世貿中心
如果恐怖份子攻擊曼哈頓的摩天大樓，飛機撞上的機率：y = 100%
恐怖份子沒有攻擊曼哈頓的摩天大樓，飛機撞上的機率（也就是意外）：z = 0.008%
後驗機率：
已知第二架飛機撞上世貿中心，對恐怖攻擊修正後的機率估計：xy / [xy + z ( 1 – x )] = 99.99%
我們都會驚恐的推論，在豔陽高照的紐約發生一次意外已經夠不可能了，第二次幾乎是真的完全不可能。
我故意挑了些有挑戰性的例子—恐怖攻擊、癌症、被背叛—是因為我想演示貝氏推理法所能處理問題的廣度。貝氏定理不是什麼神奇公式—在我們使用過的單純形式中，裡面包含的不過是加減乘除。我們必須要提供它資訊，尤其是我們對先驗機率的估計，它才能產生有用的結果。
然而，貝氏定理確實要求我要用機率來看待這個世界，就算是談到我們不願意認為是機率問題的事情也一樣。這定理沒有要求我們採取立場，去認為這個世界本質上、形而上是不確定的—拉普拉斯認為從星球的軌道到最小分子的行為，一切都是受一絲不苟的牛頓定律所支配，然而他在貝氏定理的發展上大有助益。說得更確切些，貝氏定理處理的是認識論上（epistemological）的不確定—我們知識的限制。
摘自《精準預測：如何從巨量雜訊中，看出重要的訊息？》，由三采文化出版。
