- 本文亦同步刊載於林澤民的部落格,原文標題為〈回溯推論法、貝氏定理、及推理小說〉
編按:回溯推理(或稱溯因推理)是從「證據推理到最佳解釋」的反覆過程。福爾摩斯的名言:「當你把一切不可能的情況都排除之後,那剩下的,不管多麼離奇,也必然是事實。」正點出了「回溯推理」的精隨,以及背後涉及的「貝氏定理」。
本文分為上下篇,上篇將帶領讀者熟悉回溯推理的基本概念,下篇則會運用貝氏定理分析,一窺偵探腦內的判斷機制。

福爾摩斯在《皮膚變白的軍人》案中的推理過程
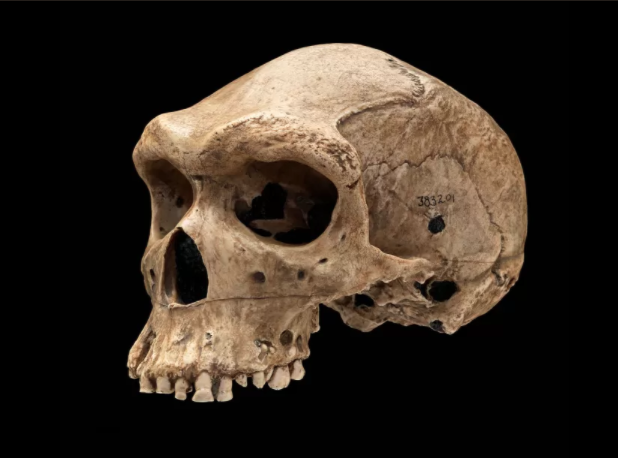
道爾的福爾摩斯故事中,福爾摩斯都用了這種方法破案。其中把這方法的應用說得最清楚的,莫過於《皮膚變白的軍人》。這個故事寫於 1926 年,是道爾晚年的作品。一般讀者對它印象可能不深,但它有一個特色:它是所有福爾摩斯小說中唯二華生未親自出現的一篇。所以,小說中推理方法的描述,是由福爾摩斯本人娓娓道來的。
故事中來向福爾摩斯求助的客戶是退伍軍人,他因與昔日同袍好友失聯,心中不安。寫信給好友父親,父親說好友周遊世界去了,一年之內不會回來。但客戶不相信好友出遊會不告知他,非常疑惑。於是轉而寫信給好友母親,詳述軍中友情,欲前往拜訪。好友母親熱情歡迎,他遂前往,並蒙留宿。
但好友父親仍然冷漠相待,只重複好友出國周遊的說法。當晚,夜深時,他彷彿看到好友隔著落地窗戶從室外看他,臉色慘白,有如鬼魂。他急忙追出,其身影已經消失在黑暗中。第二天,他厚顏要求再宿一宵,乘機觀察附近環境,發現園子盡頭有一棟房屋,有人看守,頗為神秘。他疑心好友被幽禁在此,但他的窺伺行動被好友父親發現,對他下了逐客令。他只好來求福爾摩斯相助追查真相。
福爾摩斯在揭發真相後,如此跟主人解釋他的推理過程:
「我的方法,」我說道,「就建立在這樣一種假設上面:當你把一切不可能的結論都排除之後,那剩下的,不管多麼離奇,也必然是事實。也可能剩下的是幾種解釋,如果這樣,那就要一而再、再而三地加以證實,直到最後只剩下一種具有足夠根據來支持的解釋。現在我們就用這個方法來研究一下當前這個案子。起初,提到我面前的有三種可能的解釋,可以說明為什麼這位先生在他父親莊園的小屋裡被隔離或禁錮起來。可以認為他是由於犯罪而逃避,或者是由於精神失常而不願住瘋人院,最後是因為有某種疾病而需要隔離。我想不出其它解釋。那麼,就需要把這幾個結論加以對比和甄別。
犯罪之說是不能成立的。本地區並沒有尚未破案的犯罪報告,這我十分清楚。如果說是尚未暴露出來的犯罪,那從家族利益來說應該是把他弄走或是送出國外,而不是藏在家裡。我看不出這條思路有什麼可能成立的地方。
精神失常的可能性要更大一些。小屋裡有的第二個人可能是看守人。他走出來以後把門倒鎖上,這就加強了上述假設,說明可能是強行禁閉。但另一方面,強制不可能是很嚴的,否則這個青年就不會跑出來去看一眼他的朋友了。多德先生,你記得我曾探索論據,比如問你肯特先生讀的是什麼報紙。如果是《柳葉刀》或《英國醫學雜誌》,那會幫助我思索。但是,只要有醫生陪同並上報當局,把瘋人留在家裡是合法的事。為什麼這樣拚命保密呢?因此精神失常的設想也不能成立。
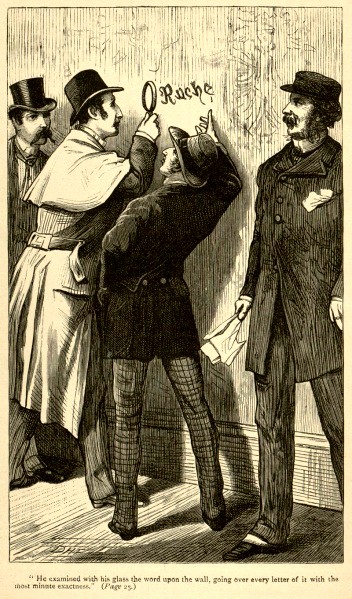
剩下的第三個可能,看來雖然稀奇,卻是完全符合實際情況的。麻瘋在南非是常見病。由於特殊的機遇,這位青年可能受到感染。這樣一來,他的家屬處境就十分困難了,因為他們不願把他交給麻瘋隔離病院。為了不露風聲、不受當局干涉,必須嚴守秘密。如果給以適當報酬,不難找到一位忠實的醫生來照顧病人。也沒有理由在晚上不讓病人出來。膚色變白是這種病的普通症狀。這個假設的論據是十分充足的,以致使我決心把它當做已被證實了那樣來行動。當我初到這裡,發現給小屋送飯的拉爾夫戴著浸了消毒水的手套,這時候我連最後的疑點也消除了。先生,我只寫了一個詞,就告訴你秘密已被發現了,我之所以寫而沒有說出來,是為了向你證明可以信任我的謹慎。
貝氏回溯推理者福爾摩斯
福爾摩斯因客戶的敘述而提出三個可能的假設,這固然是回溯推論法,但他排除其中兩個而達到一個確定的結論,其方法卻不脫演繹法。這是因為「以否定後項來否定前項」其實是具有絕對確定性的演繹邏輯:
- 前提1:若 A2 則 B2 及 B
- 前提2:¬B2
- —————————-
- 結論:¬A2
- 前提1:若 A3 則 B3 及 B
- 前提2:¬B3
- —————————-
- 結論:¬A3
如果福爾摩斯能確定他提的三個理論是互斥而且窮盡所有可能性的(mutually exclusive and exhaustive),則他所謂「當你把一切不可能的結論都排除之後,那剩下的,不管多麼離奇,也必然是事實」可以示意如下:
- 前提1:若 ¬A2 及 ¬A3 則 A1
- 前提2:¬A2 及 ¬A3
- —————————-
- 結論:A1
這樣的推論沒有任何不確定性,當然是十足的演繹法。也許這是道爾把福爾摩斯的方法稱為「演繹的科學」的原因吧?
但是這種演繹法成立的條件,除了理論必須互斥而且窮盡所有可能性之外,還得他的前提特別是對 B2、B3(或 ¬B2、¬B3)的鑑識都是百分之百確定的。如果其中有任何不確定性,例如疑犯自白、證人證詞、甚至科學鑑識的可信度不足,則使用「以否定後項來否定前項」的邏輯也就無法達到 p=1 的結論了。
《皮膚變白的軍人》案中,福爾摩斯亟想知道小屋看守人是否在讀《柳葉刀》等醫學刊物,但客戶沒去注意這些細節,隨口答了比較像《觀察家》。這種「證詞」能有多少確定性?如何足以讓福爾摩斯百分之百否定精神失常的假說?而且難道痲瘋病患者的看守人就不會讀《柳葉刀》嗎?當 0<p<1 時,我們就又回到回溯推論法了。此時因為不止一個理論無法完全排除,必須仰賴貝氏定理來算各理論的後驗機率。

貝氏定理的計算必須要假設先驗機率,其值由福爾摩斯依客戶的敘述及他自己的專業知識可以主觀判斷。
以下的例子假設犯罪逃亡(理論1)、精神失常(理論2)、傳染疾病(理論3)三個理論的先驗機率分別為Pr(1)=0.2、Pr(2)=0.3、Pr(3)=0.5。
福爾摩斯到現場調查之後,依鑑識結果判定資料支持各理論的程度。這是假設理論為真時,觀察到所得資料的條件機率。這裡依據故事中福爾摩斯自己的分析假設了下列條件機率,其中「+」代表調查所發現的資料與理論相符,「-」代表調查所發現的資料與理論不符:
- 調查結果與犯罪逃亡的理論完全不符,Pr(+|1)=0.0,Pr(-|1)=1.0。
- 調查結果與精神失常的理論不盡相符,Pr(+|2)=0.5,Pr(-|2)=0.5。
- 調查結果與傳染疾病的理論大致相符,Pr(+|3)=0.9,Pr(-|3)=0.1。
這些調查結果可以讓福爾摩斯用貝氏定理來更新他的先驗機率,其結果就是所謂後驗機率,也就是回溯推論法結論的確定性。計算的結果顯示:如福爾摩斯所說,犯罪逃亡的理論的確是不能成立的(Pr(1|+)=0),但其它兩個理論都不能完全排除。經過調查之後,資料證據稍微減少了精神失常的可能性(Pr(2|+)=0.25),但大大加強了傳染疾病的可能性(Pr(3|+)=0.75)。見表一。這結果雖然無法保證每案必破,卻比較合乎現實情況。
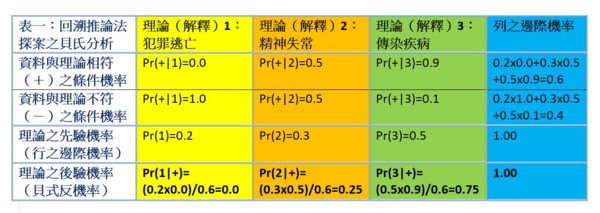
貝氏定理的計算,請參考我的文章:〈會算「貝氏定理」的人生是彩色的!該如何利用它讓判斷更準確、生活更美好呢?〉
從這個例子可以看出:不論先驗機率如何,只要資料與理論完全不符(即條件機率為零),該理論就可以完全排除。如果資料不只與犯罪逃亡的理論不符,也與精神失常的理論不符,那剩下的當然就只有傳染疾病的理論了。
這就是「當你把一切不可能的結論都排除之後,那剩下的,不管多麼離奇,也必然是事實」。
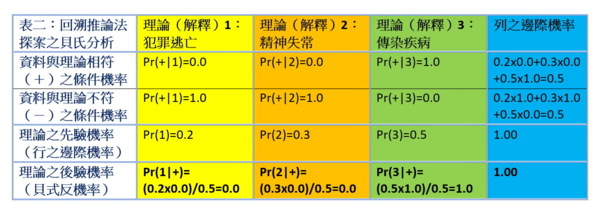
這個結論雖然在特殊的條件下用演繹法就可推出,但它其實是回溯推論法的一個特例,用貝氏定理也可算出,只是不需要那麼麻煩而已。見表二。當鑑識資料與理論的符合程度不是那麼確定時,光靠演繹法就行不通的,還是要仰賴回溯推論法及貝氏定理!
諾伯里!
太過於相信自己的判斷曾經給福爾摩斯帶來失敗的教訓。在另一個與《皮膚變白的軍人》有點類似的疑案《黃面人》中,從倫敦西南諾伯里(Norbury)區專程來求助的客戶懷疑自己的婚姻出了可怕的問題。他有次經過住家附近的一棟空屋,發現空屋的一扇窗戶裡有一張詭異的面孔也正在看著他:
我背上似乎冒出了冷汗。我站得稍微遠了一點,所以看不清面貌如何。不過這張面孔有點不自然而且不像人臉。這就是我那時的印象。我便急忙走向前去,以便把窺視我的那個人看得更清楚些。但我走近以後,那張面孔突然不見了,彷彿突然被拉到室內的暗處。我站了足有五分鐘,仔細考慮這件事,打算把我得到的印象分析一下。我很難說明這究竟是一張男人的面孔,還是女人的,它離我太遠了。可是這張面孔的顏色給我留下的印象卻是很深的。它就像青灰色的白堊土一樣,而且有點僵硬呆板,不自然得嚇人。
客戶心中不安,可是接下來發生的事更令他焦急:他發現他的美國妻子進出這棟空屋,行為異常,卻堅決不肯透露實情,只請求他相信她的愛情和苦衷。可是客戶忍不住了,來請福爾摩斯協助。
聽過客戶敘述案情之後,福爾摩斯在華生催問下,提出了他的唯一一個理論:客戶妻子的前夫住在空屋裡。華生難得地不以為然,說那完全是臆測,但福爾摩斯說:
「可是它至少符合所有的事實。假使再發現了不相符合的新情況,我們重新考慮也還來得及的。」
可是福爾摩斯和華生搭火車到達當地之後,在月台等待的客戶「面色蒼白,憂心忡忡,渾身顫抖」已經忍無可忍了,要求兩人為證,直接闖入空屋。這才發現黃面人是妻子與美國具非洲血統的前夫所生的小女孩。
前夫雖然膚色不黑,小女孩卻黝黑得多,妻子怕鄰居的流言蜚語,給女孩戴上黃色的面具,讓她至少可以在窗戶後面窺視戶外景物。客戶諒解妻子的苦衷,抱著小孩與妻子攜手回家。
福爾摩斯不發一言回到倫敦,直到夜晚,才對華生說:
「如果以後你覺得我過於自信我的能力,或在辦一件案子時下的功夫不夠,請你最好在我耳旁輕輕說一聲『諾伯里』,那我一定會感激不盡的。」