- 本文亦同步刊載於林澤民的部落格,原文標題為〈回溯推論法、貝氏定理、及推理小說〉
編按:回溯推理(或稱溯因推理)是從「證據推理到最佳解釋」的反覆過程。福爾摩斯的名言:「當你把一切不可能的情況都排除之後,那剩下的,不管多麼離奇,也必然是事實。」正點出了「回溯推理」的精隨,以及背後涉及的「貝氏定理」。
本文分為上下篇,上篇將帶領讀者熟悉回溯推理的基本概念,下篇則會運用貝氏定理分析,一窺偵探腦內的判斷機制。

「你要知道,我親愛的華生,」他把試管放回架子上去,開始用教授對他班上的學生講課的口氣往下說,「作出一串推理來,並且使每個推理取決於它前面的那個推理而本身又簡單明瞭,實際上這並不難。然後,只要把中間的推理統統去掉,對你的聽眾僅僅宣佈起點和結論,就可以得到驚人的、也可能是虛誇的效果。所以,我看了你左手的虎口,就覺得有把握說你沒有打算把你那一小筆資本投到金礦中去,這真的不難推斷出來。」
「我看不出有什麼關係。」
「似乎沒有,但是我可以馬上告訴你這一密切的關係。這一根非常簡單的鏈條中缺少的環節是:第一,昨晚你從俱樂部回來,你左手虎口上有白粉;第二,只有在打台球的時候,為了穩定球桿,你才在虎口上抹白粉;第三,沒有瑟斯頓作伴,你從不打台球;第四,你在四個星期以前告訴過我,瑟斯頓有購買某項南非產業的特權,再有一個月就到期了,他很想你跟他共同使用;第五,你的支票簿鎖在我的抽屜裡,你一直沒跟我要過鑰匙;第六,你不打算把錢投資在南非。」
「這太簡單了!」我叫起來了。
——柯南.道爾《跳舞的人》
回溯推理的偵探:杜彭、福爾摩斯、馬婁
所謂「回溯推論法」(abduction)是有別於演繹法(deduction)和歸納法(induction)的一種推理方法,但它常被與演繹法或歸納法混淆。
回溯推論法被提出為一種科學研究的推論方法,就我個人所知,最早見於美國哲學家 Charles Sanders Peirce (1839-1914)1878 年發表的科普文章〈Illustrations of the Logic of Science – Deduction, Induction, and Hypothesis〉。但在這篇文章裡,Peirce 用了 hypothesis(假說)這個字來稱呼回溯推論法。後來他改用 retroduction,而且一直到1896年都還用這個字。要在他 1903 年的文章,我才看到abduction這個字的出現。但不論使用哪個名詞,他都把它與演繹法及歸納法並列,作為推論方法的一種形式。
其實就在Peirce還在掙扎著釐清他用不同字眼所指涉的回溯推論法的時候,這個方法的基本形式早就廣泛地被推理小說中虛構的偵探有意識地用作辦案的方法了。這包括埃德加.愛倫.坡(Edgar Allan Poe)筆下的杜彭(Dupin)和柯南.道爾(Conan Doyle)筆下的福爾摩斯(Holmes)。杜彭號稱小說界第一位偵探,但他只出現在 1841-1844 出版的三篇短篇小說中。反觀福爾摩斯,他一共出現在 4 篇長篇及 56 篇短篇裡,其出版年份縱貫 1887-1927。當華生(Watson)已經很清楚地介紹福爾摩斯的探案方法的時候,Pierce 還沒拿定用哪個字眼來稱呼這個方法較恰當。
這就難怪華生把福爾摩斯的推理方法稱為「演繹的科學」(the science of deduction)囉。
不僅小說家會把回溯推論法與其它推論方法混淆,即便學界大師也會搞錯。因果論大師朱迪亞.珀爾(Judea Pearl)便把福爾摩斯的方法稱為歸納法。他在《因果革命:人工智慧的大未來》(The Book of Why: The New Science of Cause and Effect)一書中寫道:「但福爾摩斯真正厲害的,不是由假說演繹出結論,而是歸納。歸納法的運作方向和演繹法相反,是從證據產生假說。」
沒錯,回溯推論法簡單說是「從證據產生假說」。但歸納法是要從統計資料產生通則,而回溯推論法則是要從不斷更新的事實推出最可能的解釋。這些解釋不必是通則:它們可能只是無法觀察到的事實。
科學家要建立通則;偵探對通則沒有興趣,他們有興趣的是事實,特別是未能觀察到的事實。
也是偵探小說作家的雷曼.錢德勒(Raymond Chandler)透過他筆下的偵探馬婁(Marlowe)說:「有些事情是事實:在統計的意義上、寫在紙上、錄在帶上、作為證據的事實。而有些事情之所以為事實是因為缺少了它其它的事情就無法解釋了。」(《回播》)
當然馬婁這話令人想到福爾摩斯的名言:
「當你把一切不可能的情況都排除之後,那剩下的,不管多麼離奇,也必然是事實。(When you have eliminated the impossible, whatever remains, however improbable, must be the truth.)」(《四簽名》)
在《血字的研究》一書中,福爾摩斯進一步地對華生解釋他的方法:
我已經對你說過,凡是異乎尋常的事物,一般都不是什麼阻礙,反而是一種線索。在解決這類問題時,最主要的事情就是能夠用推理的方法,一層層地回溯推理。這是一種很有用的本領,而且也是很容易的,不過,人們在實踐中卻不常應用它。在日常生活中,向前推理的方法用處大些,因此人們也就往往容易忽略回溯推理這一層。如果說有五十個人能夠從事務的各個方面加以綜合推理的話,那麼,能夠用分析的方法推理的,不過是個把人而已。
我也很難指望你能夠弄得清楚。讓我試試看我是否能夠把它說得更明確一些。大多數人都是這樣的:如果你把一系列的事實對他們說明以後,他們就能把可能的結果告訴你,他們能夠把這一系列事實在他們的腦子裡聯繫起來,通過思考,就能得出個什麼結果來了。但是,有少數的人,如果你把結果告訴了他們,他們就能通過他們內在的意識,推斷出所以產生出這種結果的各個步驟是什麼。這就是在我說到『回溯推理』或者『分析的方法』時,我所指的那種能力。
偵探小說中,逆向推理首見於愛倫.坡的杜彭。《血字的研究》中福爾摩斯嘲笑杜彭「賣弄」(showy)、「膚淺」(superficial)、「不入流」(inferior),但也不得不承認杜彭分析問題的天才。我們讀杜彭的故事,讀到他在首次出現時,精準逆推敘述者思路的情節,可以想像道爾完全是在模仿愛倫.坡。如果那是賣弄,那福爾摩斯逆推華生思路的賣弄比起杜彭只有過之。
演繹法、歸納法、回溯推論法的差異
回溯推論法與演繹法、歸納法的區別可以用不同組合的三段論來闡釋。
演繹法
- 前提 1:若 A 則 B
- 前提 2:A
- ———————
- 結論:B
歸納法
- 前提 1:A
- 前提 2:B
- ==========={p}
- 結論:若 A 則 B
回溯推論法
- 前提 1:若 A 則 B
- 前提 2:B
- ==========={p}
- 結論:A
這裡「==={p}」代表結論不是絕對的, 而是只有機率0<p<1的「確定性」。
以邏輯學常用的例子 A=「天雨」、B=「地濕」來看。如果演繹法的兩個前提(「若天雨,則地濕」及「天雨」)都成立,其結論(「地濕」)是百分之百(p=1)確定的,不必用「==={p}」的符號來表示。
我們即使在很多不同的時空裡觀察到「天雨」跟「地濕」的連結,但我們仍然不能藉由資料本身就確定「若天雨,則地濕」是一個放諸四海皆準的通則。歸納法出錯的有名例子是「黑天鵝」事件。當 1967 年荷蘭探險家 Willem de Vlamingh 在澳洲看到黑天鵝的時候,歐洲人才知道他們以有限的經驗事實歸納出的「所有的天鵝都是白色的」的結論是錯誤的。
回溯推論法同樣不能導出百分之百確定的結論,但上述回溯推論法的三段論與歸納法有明顯的不同。光以三段論來看,回溯推論法與演繹法毋寧是比較接近的:它們都以通則「若 A 則 B」為前提,只是演繹法是由A來推論B,而回溯推論法是由B來推論A。從邏輯上來說,回溯推論法當然是不對的。我們都知道「若 A 則 B」只能引申出「若 ¬B 則 ¬A」(¬是邏輯中「非」的符號),亦即「以否定後項來否定前項」(modus tollens)而不能以肯定後項來肯定前項。
「地濕」無法推出「天雨」的結論,這是明顯的道理:因為「地濕」有許多原因,「天雨」只是其中之一而已。既然如此,那回溯推論法究竟有沒有邏輯上的價值?
回溯推論法的價值不是建立在單一的三段論上面,它仰仗的是當新事實出現時,這三段論的反覆應用。舉例來說,假設有而且只有三個事實 A1、A2、A3 能產生B的結果,但它們各自也能分別產生B1、B2、B3的結果。如此則我們有三個通則:「若 A1 則 B1 及 B」、「若 A2 則 B2 及 B」、「若 A3 則 B3 及 B」。當我們只觀察到 B 時,回溯推論法讓我們得到 A1、A2、或 A3 的結論,但卻無法告訴我們其中何者為真。
- 前提 1:若 A1 則 B1 及 B
- 前提 2:若 A2 則 B2 及 B
- 前提 3:若 A3 則 B3 及 B
- 前提 4:B
- ——————————
- 結論:無單一對應結果
但當我們觀察到更多的事實時,我們也許就能得到較為確定的結論。例如我們在觀察到 B 的同時也觀察到 B1,則結論為 A1 的確定性將會提高。但即使我們未觀察到B1,如果能觀察到B2、B3的反證,則A2、A3可以被否定,A1的確定性將提高至 p=1。後者的推論方法可以示意如下:
- 前提 1:若 A1 則 B1 及 B
- 前提 2:若 A2 則 B2 及 B
- 前提 3:若 A3 則 B3 及 B
- 前提 4:B
- 前提 5:¬B2
- 前提 6:¬B3
- ——————————
- 結論:A1
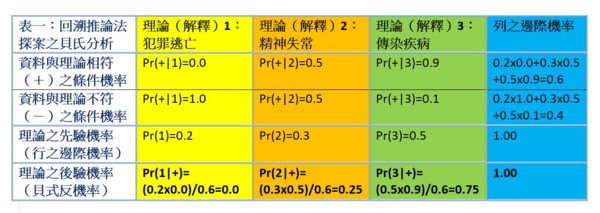
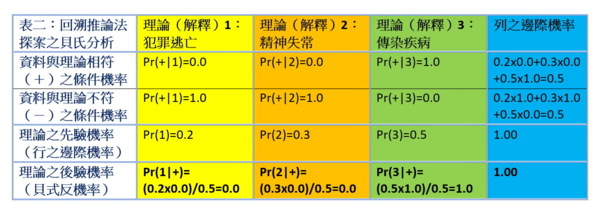
在福爾摩斯的方法論中,他把 A1、A2、A3稱作「理論」(theory),有時也稱作「假說」(hypothesis)或「解釋」(explanation),把B1、B2、B3稱作「資料」(data)。
登門求助的客戶訴說犯罪現場的狀況後,福爾摩斯有了基本資料。如果基本資料足夠,他會形成幾個有待進一步驗證的理論。但如基本資料不夠,他通常不願立刻提出理論,而寧可等待到現場蒐集進一步資料後再提出理論。此時理論可能仍有好幾個,他會不斷地努力追求新資料,例如拿放大鏡匍匐在地上觀察足跡、塵土、煙灰等等。這些動作雖然常被蘇格蘭場的警探嘲弄,他的目的就是要有更多的事實資料來讓他增加或減少某些理論的確定性。到最後如果某理論達到 p=1,他就破案了。