在網際網路發達的現代,私刑正義一直是社會議題值得被重視的一塊。當名人、演員、政治人物,甚至是個沒沒無聞的小卒犯錯時,許多人蜂擁到他們的社群媒體攻擊、肉搜、堵人等等,是一件值得被重視的議題。
在這一篇文章中,我將從一些心理學研究,探討「私刑正義」的可能成因,以及可能削減私刑正義的方式。
為什麼我們會想伸張正義?
人們對於不公平,似乎有著天生的敏感度。有一個德國萊比錫的研究團隊,就針對小孩子進行研究。他們讓小孩子看木偶劇場,有些木偶會對小孩子很親切,也就是所謂的好木偶,也有一些木偶會送小孩子禮物,再把禮物搶走,也就是所謂的壞木偶。

實驗者發現,當孩子看到好木偶被毆打時,他們會不開心;但是看到壞木偶被毆打時,則會雀躍不已。
實驗者好奇的是,我們是否願意花錢,來換取觀看壞人被打呢?他們在壞木偶要被懲罰的剎那,將布幕拉上,除非孩子交出手上的代幣,否則就無法繼續觀看。
結果,孩子們紛紛交出了手上的代幣,以求繼續觀看壞木偶被打[1]。
然而,這篇實驗僅能解釋,當欺負我們的人跟被懲罰的人是同一個人時,我們先天就很樂見他們被懲罰,甚至是犧牲自己的利益也在所不惜。
但是,當我們只是袖手旁觀的第三者時,為何我們依然會希望伸張正義呢?神經心理學家 Lisa Barret 對此提出了解釋[2]。
Lisa Barret 指出,人們的腦容量是有限的,正因為如此,我們不能等自己被攻擊了,才要求別人對這些人做出懲罰,而是希望「當和我們類似的人受到攻擊時,那些犯罪者能夠得到報應,以避免我們自身也受到攻擊。」
因此,當我們對某個人的受罰為之叫好時,肯定是因為他們所損害的他人利益,和我們自身有關。
這就是為什麼比起開車族、機車族,平常徒步走在街上的行人,對於警察針對行駛人行道的汽機車加強取締時,人們會更為振奮的緣故。

同情心,或許可以撫平報復心理
然而,並不是所有人,都能等待警察、法官等等來懲罰犯罪者,私刑正義的新聞我們可是時有所聞,例如先前一則疑似女兒被性侵後自殺,父親烙人抓人虐殺犯人的新聞,就在社會版面轟動一時。有些人為之叫好,但也有些人擔心「私刑正義」的嚴重性。
事實上,精神病學講師 James Kimmel Jr. 便曾指出,過度沉迷於私刑正義的結果,可能會導致「恐怖主義、復仇謀殺、幫派犯罪」等等的發生[3]。
那麼,有什麼可以避免私刑正義呢?有一篇研究指出,也許同情心是一個可能的解決之道[4]。
在這份研究中,實驗者招來了 44 名受試者,並將他們隨機分配到三種實驗情境中。在三種實驗情境裡,他們都必須要完成一份測驗,該份測驗是 20 題數學題,而他們都被安排坐在一男一女中間。
受試者不知道的是,那一男一女都是實驗者安排好的演員。
實驗開始了,在考卷發下去之前,女演員都會用眼藥水讓自己裝哭,並表示需要離開實驗。在實驗組裡面的女演員會裝作是得知哥哥得了癌症,自己卻要周末才能返家,此刻時在無法控制住自己的情緒;在控制組裡面,女演員則會裝作要趕著去看醫生,必須離開實驗室。

接著,受試者和男演員留在教室內,開始做那 20 題數學題,做了 4 分鐘,實驗者就會走過來,先收走受試者的問券,並檢查完答案後將答案卷用碎紙機碎掉,接著給他答對題數所應得的獎金。此時,實驗者會裝作身上的獎金不夠,必須要離開去拿獎金。
在實驗組中,實驗者離開之後,男演員會自己把答案卷碎掉,並在實驗者回來後,告訴對方「為了省時間,我自己對了答案,結果 20 題全對,我要領取 20 題的獎金。」並真的順利將獎金領走。
在控制組當中,男演員不會碎掉答案紙,而是表示自己比受試者多對了一題,然後領走獎金。
給予受試者報復機會
實驗者接著讓受試者有機會調配味覺測試的材料,並且讓受試者得知,這瓶材料將會讓作弊的男演員喝下,且對方不會知道是他調的。同時受試者也會知道,男演員超級怕辣。

透過這三種情境測試,實驗者想觀察兩件事情:
- 受試者是否會因為對方作弊,而想要懲罰對方?
- 受試者是否會因為剛剛另一位成員因哥哥癌症離去,而產生同情心(compassion),進而原諒作弊者的行為?
同情心可能會讓我們心軟
結果發現,在控制組裡面,受試者平均加入了 2 公克多的辣椒醬,而在實驗組裡面,受試者平均加入了將近 10 公克的辣椒醬,可見受試者對於報復作弊者,是確實會付諸行動的。
問題來了,這些受試者如果先前受到另一位演員的影響,是否會減少加入辣椒醬的量?如果是的話,這也表示,我們會因為自身的同情心,而減少對其他人的報復舉動。
研究結果顯示,同情心確實會有這樣的作用。參與到同情心實驗組的受試者,確實加入了較少的辣椒醬,只有平均約 3 公克左右,和控制組差不多。
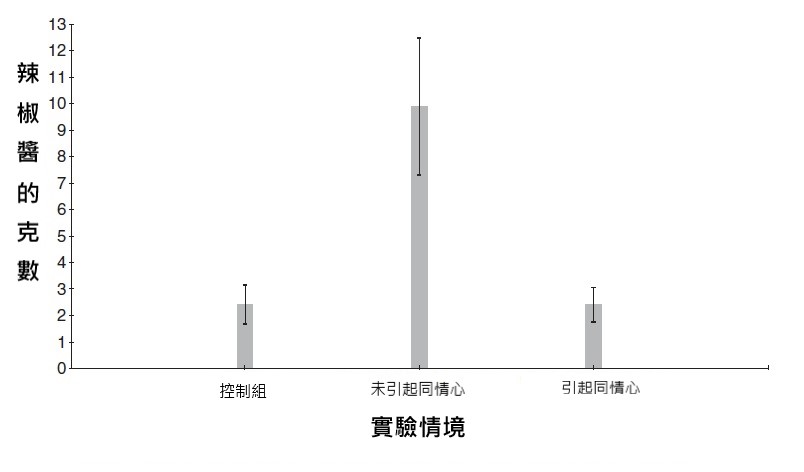
這樣的研究結果顯示了,也許同情心,真的能讓我們更加寬容地看待這個社會,不再那麼執著於懲罰受試者。
不過,實驗者也特別強調,本篇研究的「同情對象」和「我們想報復的對象」是不同人。如果是同一個人的話,我們會有什麼舉動,其實是值得再進一步探討的。
參考資料
- Natacha Mendes et al., ‘Preschool children and chimpanzees incur costs to watch punishment of antisocial others,’ Nature Human Behaviour, vol. 2, 2018, pp. 45-51.
- Lisa Feldman Barrett, How Emotions Are Made: The Secret Life of The Brain, Macmillam, London,2017,p.73.
- K.M. Carlsmith et al.., ‘The paradoxical consequences of revenge’, Journal of Personality and Social Psychology, vol.95(6), pp.1,316-24.
- Condon, Paul & Desteno, David. (2011). Compassion for one reduces punishment for another. Journal of Experimental Social Psychology.