減碳新招:二氧化碳再利用!光觸媒材料可以把二氧化碳還原成工業化學原料?——專訪中研院原分所陳貴賢特聘研究員

本文轉載自中央研究院「研之有物」,為「中研院廣告」
- 採訪撰文|簡克志
- 責任編輯|簡克志
- 美術設計|蔡宛潔
降低碳排還不夠,奈米材料幫你直接減少二氧化碳!
氣候變遷問題日益嚴重,2023 年 9 月成為全球有史以來最熱的月份,臺灣夏天飆破 38 ℃ 的頻率逐漸增加。為了避免地表升溫超過工業化前水準的 +1.5 ℃,世界各國訂出 2050 年淨零排放的目標,設法減少大氣中的溫室氣體。減碳解方除了低碳電力之外,直接減少二氧化碳也是一條路徑。中央研究院「研之有物」專訪院內原子與分子科學研究所陳貴賢特聘研究員,他的研究專長是奈米能源材料,我們將介紹一種複合光催化材料:硫化鋅(ZnS)/硫化銦鋅(ZnIn2S4,簡稱 ZIS),在太陽光照射下,此材料表面發生的氧化還原反應,會將二氧化碳還原成有用的工業化學原料!
 為了避免全球升溫超過工業化前水準的 +1.5 ℃,我們需要減少碳排放與開發負碳技術,並盡量在 2050 年左右達到全球溫室氣體淨零排放量的目標。所謂的「工業化前水準」是指 1850-1900 年的平均溫度。
為了避免全球升溫超過工業化前水準的 +1.5 ℃,我們需要減少碳排放與開發負碳技術,並盡量在 2050 年左右達到全球溫室氣體淨零排放量的目標。所謂的「工業化前水準」是指 1850-1900 年的平均溫度。
圖|iStock
地球「保冷」計畫——減碳是關鍵
我們每天排放多少二氧化碳?根據 Our World in Data 的人均二氧化碳排放數據,2021 年全球每人排放的二氧化碳為 4.69 噸,而燃燒 1 公升的汽油大概會產生 2.3 公斤的二氧化碳。換算一下,每人每天排放二氧化碳約為 12.8 公斤,相當於每人每天消耗 5.6 公升的汽油!
根據聯合國政府間氣候變化專門委員會(IPCC)的特別報告「全球暖化 1.5 ℃」,人類活動排放的溫室氣體,已經讓地球表面平均溫度上升了 1 ℃。若以人類目前經濟模式發展下去,碳排放量可預期將不斷上升,大量溫室氣體將讓暖化現象與極端天氣事件更加劇。
氣候科學家警示,地球表面平均溫度需控制在 +1.5 ℃ 以內 註 1,否則將有不可逆的後果,例如生物多樣性大幅度降低的風險。因此,世界各國有了 2050 年淨零排放的共同目標,並不是說都不排碳了,而是要設法讓溫室氣體的碳排放量和碳減少量相互抵消,達到「淨零」的目標。
要達到淨零的目標,除了尋找與開發減碳電力之外,直接減少二氧化碳也是一個方法。想像一下,如果可以像植物一樣,只要照太陽光,就把二氧化碳變成有價值的碳氫化合物,聽起來不錯吧?但是二氧化碳做為燃燒後的產物已相當穩定,要如何以人工方式讓二氧化碳再次參與反應?
我們可運用「陽光」與「光催化材料」(又稱光觸媒,photocatalyst),不僅可以減碳,還能產生有價值的碳氫化合物,是一種「一舉兩得」的方法!
光觸媒(光催化)材料是什麼?
在談到光催化材料之前,先複習一下「催化劑」這個概念,催化劑不參與化學反應,但是它讓原先不可能的化學反應變得可行!陳貴賢分享,這就像過去從臺北到宜蘭需要翻過雪山,經過九彎十八拐的北宜公路;但如今有了「雪山隧道」之後,就大大降低臺北到宜蘭的時間與難度。「雪山隧道」就是臺北通往宜蘭的催化劑。
除此之外,催化劑也可以說是推進人類歷史發展的重要角色!在過去,農作物施肥只有天然氮肥可以使用,產量有限。而肥料意味著糧食增加與生產力增加,《巫師與先知》這本書就提到位於秘魯的鳥糞島嶼成為各家跨國公司必爭之地。另一方面,波斯人也在各地建造供鳥類休息的高塔,用來收集當肥料用的鳥糞。
到了近代,陳貴賢提到在 20 世紀初,德國科學家哈伯(Fritz Haber)透過催化劑,在高溫高壓的條件下,以鐵粉做為催化劑,讓氮氣和氫氣轉換成氨。這讓人工固氮成為可能,人類不用再依賴緩慢的生物固氮反應就可以合成化學氮肥,農作物產量也大幅提昇。
本文主角「光催化材料」,顧名思義就是協助光化學反應的催化劑,但光催化材料與一般催化劑不同的地方在於,其化學反應通常發生在固態的表面環境,目標反應物、光子和電子都有參與反應。
比起光催化材料,你可能更常聽到它的同義詞「光觸媒」,例如某某產品宣稱具有「奈米光觸媒消毒」的功能,其實就是照射足夠的光,讓材料表面的氧化還原反應把細菌分解。而之所以光觸媒需要做到奈米尺寸,這是因為奈米小顆粒可以改變物質的電子能量結構,且大幅增加反應的表面積,讓光催化反應更有效率。
陳貴賢:「一個高表面積的奈米粉末,它的表面積可能是薄膜的一萬倍,甚至於十萬倍。」
給你電子,還你原形!光催化材料上的氧化還原反應是怎麼發生的?
光催化材料之所以能夠減少二氧化碳,是因為照光後材料表面發生「氧化還原反應」,氧化反應會失去電子,還原反應會得到電子。陳貴賢與團隊開發的複合光催化材料:硫化鋅(ZnS)/硫化銦鋅(ZnIn2S4,簡稱 ZIS),可以讓二氧化碳還原成甲醇(CH3OH)和乙醛(CH3CHO),這兩種產物都是工業常用的化學原料。反應式如下:
要持續減少二氧化碳,就要持續發生上述還原反應,持續供給電子。不過,我們要怎麼讓電子快速又順利的補充到材料表面?這裡就開始涉及到半導體的核心問題:電子與電洞的產生、分離和傳輸。
陳貴賢與團隊開發的複合光催化材料:ZnS/ZIS,是結合兩種奈米半導體材料,透過水熱法合成,將 0 維的 ZnS 奈米顆粒沉積在 2 維的 ZIS 奈米片之上,形成 0D-2D 結構的 ZnS/ZIS 複合物,就像製作巧克力豆餅乾,不過要複雜得多。
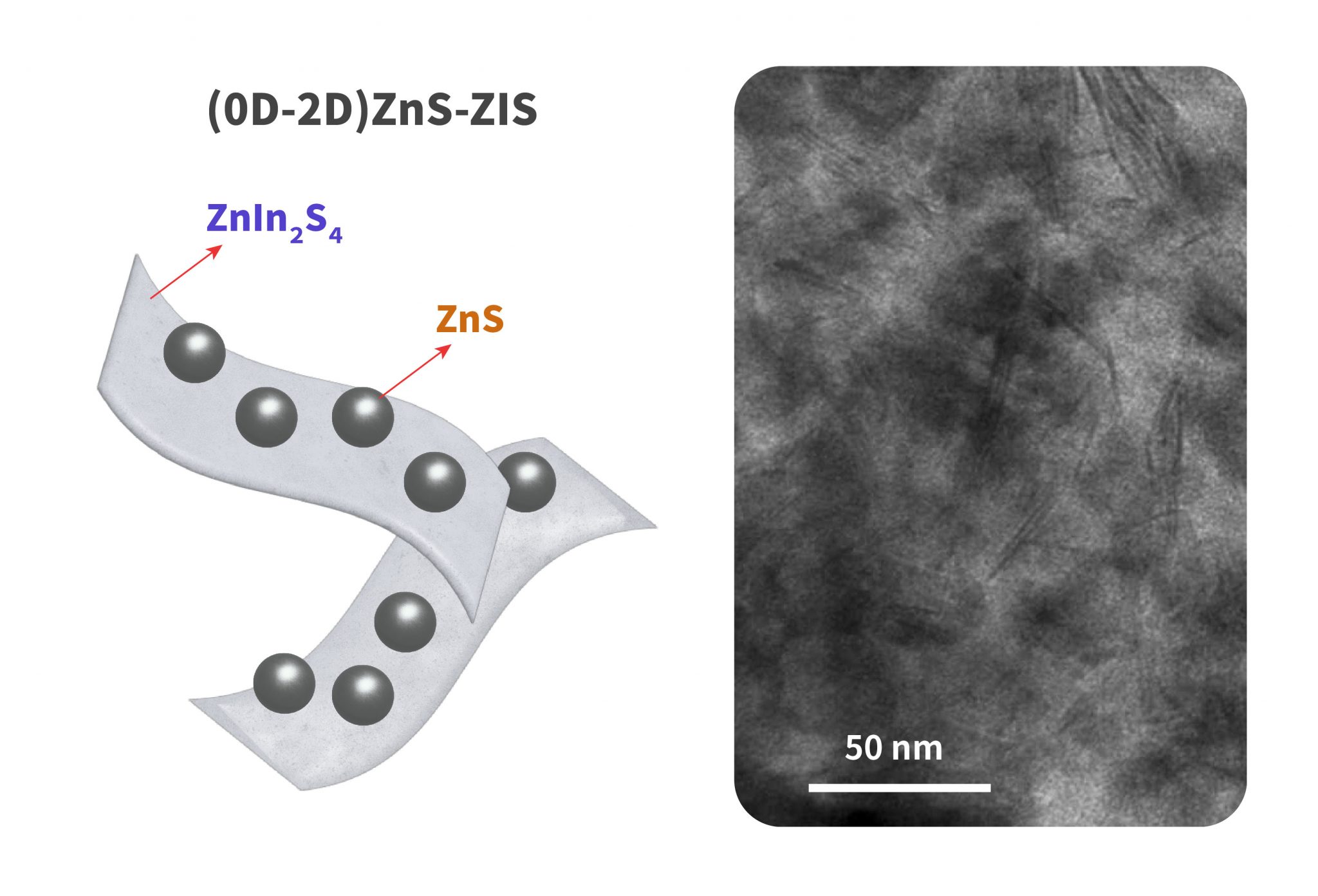
 陳貴賢團隊將 0 維的 ZnS 奈米顆粒沉積在 2 維的 ZIS 奈米片之上,就好像做巧克力豆餅乾一樣,形成複合的異質半導體,做為光催化材料用途。左圖是示意圖,右圖是電子顯微鏡下的照片,Zn:In 比例為 1:0.46。
陳貴賢團隊將 0 維的 ZnS 奈米顆粒沉積在 2 維的 ZIS 奈米片之上,就好像做巧克力豆餅乾一樣,形成複合的異質半導體,做為光催化材料用途。左圖是示意圖,右圖是電子顯微鏡下的照片,Zn:In 比例為 1:0.46。
圖|研之有物(資料來源|Nano Energy)
既然 ZnS/ZIS 是半導體,當受到光照之後,原來的價帶(valence band)電子會被光激發成導帶(conduction band)電子,原本價帶電子佔據的位置則留下一個空位,就是電洞。電子和電洞的遷移,就是半導體形成電流的原因,因此電子和電洞都稱為「載子」(charge carrier)。
還記得上面的還原反應嗎?
對光催化材料來說,為了在光照環境下把二氧化碳還原成乙醛和甲醇,必須獲得穩定的電子來源,材料內部要迅速補充電子到表面,因此:
照光產生的電荷載子數量越多越好;產生的電子和電洞要傾向分離,分得越遠越好;電子和電洞越快移動到表面參與反應越好。
載子輸送要快速穩定,首先照光產生的載子要多,就有更多電子和電洞參與反應。分離載子是為了避免復合,照光產生的電子和電洞很容易復合,一旦復合,等同於減少載子。再來是載子越快移動到表面越好,可以讓每次的氧化還原反應都是最佳效率。
尋找最有效的光催化材料
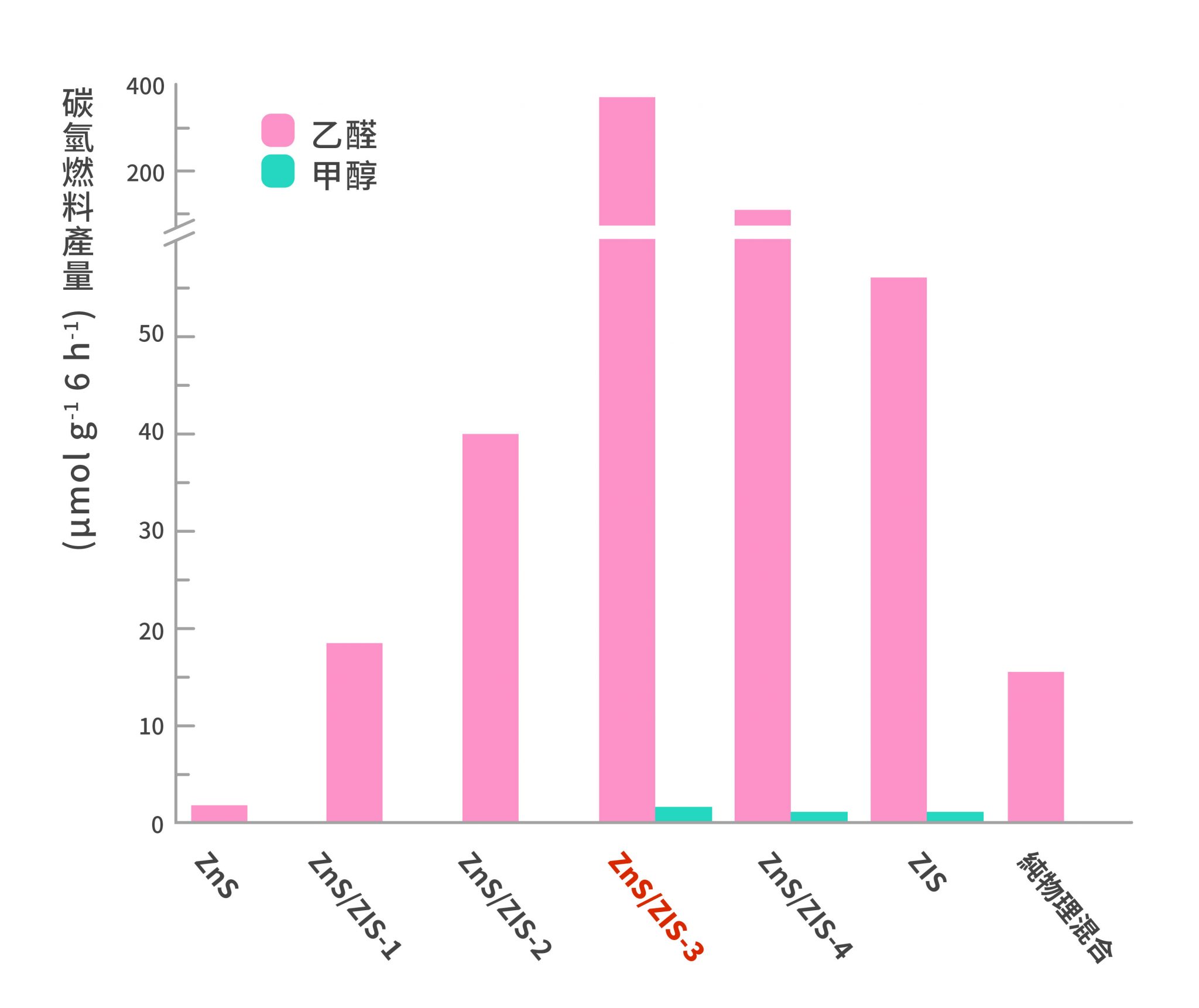
陳貴賢團隊總共做了 4 種不同比例的 ZnS/ZIS 光催化材料,依照 Zn:In 比例 1:0.12、1:0.26、1:0.46 和 1:0.99,分別標記為 ZnS/ZIS-1、ZnS/ZIS-2、ZnS/ZIS-3 和 ZnS/ZIS-4。其中,ZnS/ZIS-3 的光催化效果最好,可以有效減少二氧化碳,產生最多的乙醛和甲醇(如下圖)。
 水熱法製備的 ZnS/ZIS-3 光催化效果最好,可以有效減少二氧化碳,產生最多的乙醛和甲醇。最右邊是將 ZnS 和 ZIS 簡單物理混合的對照組,沒有介面效應的輔助,催化效果不佳。
水熱法製備的 ZnS/ZIS-3 光催化效果最好,可以有效減少二氧化碳,產生最多的乙醛和甲醇。最右邊是將 ZnS 和 ZIS 簡單物理混合的對照組,沒有介面效應的輔助,催化效果不佳。
圖|研之有物(資料來源|Nano Energy)
為了驗證光催化材料產生有效載子的效率,陳貴賢團隊計算了 ZnS/ZIS-3 的總 AEQ 值(apparent quantum efficiency),用來評估「照到光催化材料上的每顆光子數量,產生了多少實際參與催化反應的電子數」。測量之後,ZnS/ZIS-3 的 AEQ 值為 0.8%,量子效率比單獨的 ZnS 材料提高了將近 200 倍!
這也是為什麼陳貴賢團隊要使用兩種不同的材料結合,因為單一半導體材料照光產生的電子和電洞有很高的復合機率,選擇兩種不同的半導體材料組合,讓兩種材料形成特殊的「能量階梯」就可以有效分離電子和電洞,並且把電子送到它該去的材料表面。
此外,使用兩種半導體材料的好處還有「二次激發電子到更高能階」,以符合光催化反應的能量門檻,自由電子掙脫 ZnS 的束縛之後,繼續往 ZIS 跑,光的能量會繼續把電子往上送到更高能級的材料表面,還原二氧化碳的反應在此發生。
Z 字形跑比較快!控制材料之間的微應變提升氧化還原效率
關於光催化材料的二次激發,陳貴賢提到:「材料低能階,然後光子進來後,把電子激發到高能階去做反應,太陽能電池也是這樣。但是呢,有時候沒那麼剛好,例如激發後的能階不夠高,雖然激發上去了,但電子沒有辦法跟二氧化碳做反應。那我把兩個材料拼在一起,電子上去以後又下來,然後再吸收第二個光子上去,那就變得很高了,高了以後它的反應效率就提升很多。」
如果我們把光催化材料的二次激發過程畫成示意圖,如下圖所示,電子在 ZnS 束縛區受到第一次光子的激發,變成自由電子,接著經過設計完善的材料介面,先降到較低的 ZIS 束縛區,受到第二次光子的激發,再次變成自由電子,跑到光催化材料的表面,和二氧化碳發生還原反應,將二氧化碳變成可再利用的乙醛和甲醇。
看看電子走過的路,如果向左歪著頭看,是不是就是一個 Z 字呢?科學家把這個過程稱為「直接 Z 方案」(Direct Z-scheme)。「直接」的意思是,電子從 ZnS 跑到 ZIS 的過程,不需要再經過一個中間地帶,降低電子和電洞復合的機會。
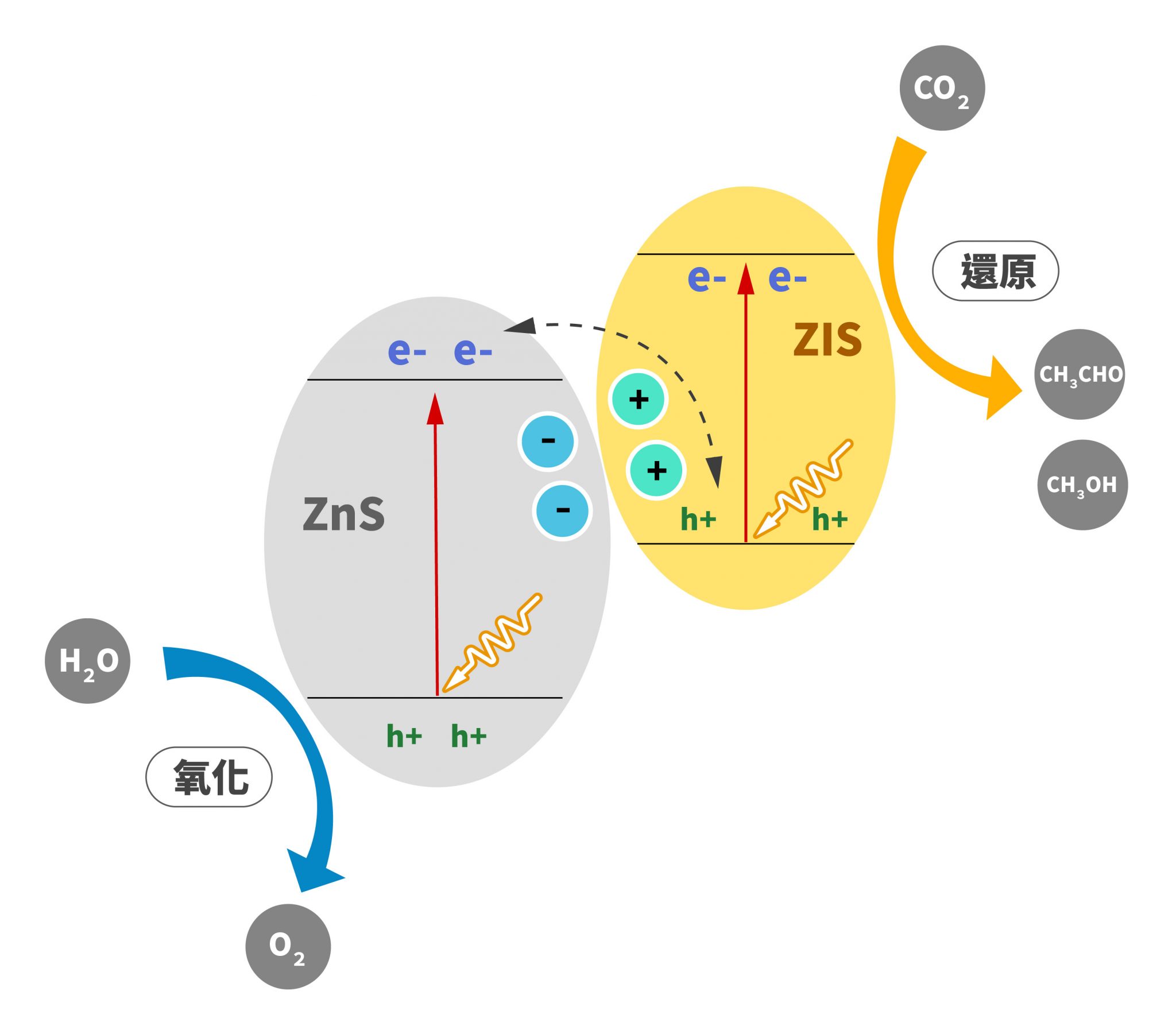
 為了將二氧化碳轉換成可用化學原料,電子在材料內部能階走 Z 字路徑,過程中受到光的二次激發,最後到達材料表面。電子參與還原反應,將二氧化碳變成乙醛和甲醇。電洞參與氧化反應,將水變成氧氣。
為了將二氧化碳轉換成可用化學原料,電子在材料內部能階走 Z 字路徑,過程中受到光的二次激發,最後到達材料表面。電子參與還原反應,將二氧化碳變成乙醛和甲醇。電洞參與氧化反應,將水變成氧氣。
圖|研之有物(資料來源|Nano Energy)
為什麼陳貴賢團隊設計的「直接 Z 方案」光催化材料,電子可以不需要中間的「轉接站」,直接轉移到另一個材料上呢?這裡也有一個巧思:不同材料之間的「微應變」。
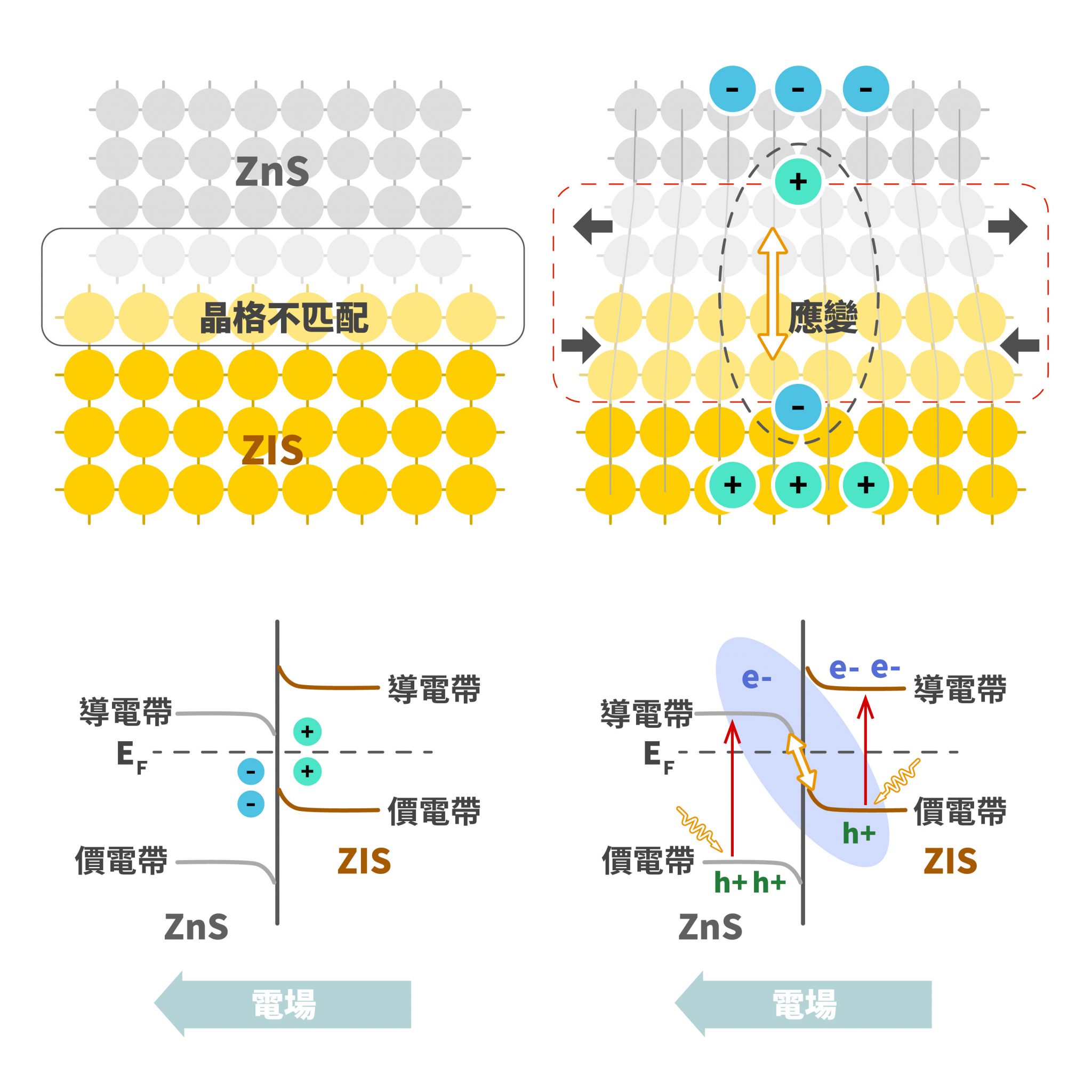
不同材料的晶體排列規律是不一樣的,當兩種材料接在一起時,接面處會發生「晶格不匹配」,也就是兩種材料的原子會互相卡到、晶格微微變形。但是,如果我們可以控制微應變(Strain)的程度,就可以控制兩種材料「能量階梯」的相對位置,微應變可以讓材料接面自動帶有「轉接站」的功能,進而形成一個內部電場,讓電子和電洞更能快速分離,提高光催化效率。
總之,陳貴賢團隊開發的這套材料組合,是有微應變誘導的直接 Z 方案光催化材料,可做為未來量產光催化材料的研發設計參考,同時也是減碳的解方之一。
 ZnS 奈米顆粒接在 ZIS 奈米片上,兩邊的晶格排列方式不一樣,發生「晶格不匹配」,接面處晶格會微微變形。如果控制微應變(Strain)的程度,就可以微調材料能階的相對位置,微應變可以讓接面帶有「轉接站」的功能,形成一個內部電場,讓電子和電洞更能快速分離,提高光催化效率。
ZnS 奈米顆粒接在 ZIS 奈米片上,兩邊的晶格排列方式不一樣,發生「晶格不匹配」,接面處晶格會微微變形。如果控制微應變(Strain)的程度,就可以微調材料能階的相對位置,微應變可以讓接面帶有「轉接站」的功能,形成一個內部電場,讓電子和電洞更能快速分離,提高光催化效率。
圖|研之有物(資料來源|Nano Energy)
ZnS 奈米顆粒接在 ZIS 奈米片上,兩邊的晶格排列方式不一樣,發生「晶格不匹配」,接面處晶格會微微變形。如果控制微應變(Strain)的程度,就可以微調材料能階的相對位置,微應變可以讓接面帶有「轉接站」的功能,形成一個內部電場,讓電子和電洞更能快速分離,提高光催化效率。
圖|研之有物(資料來源|Nano Energy)
綠能趨勢——光催化材料未來可期
陳貴賢表示,目前表面科學和材料是中研院原分所的主要研究領域,他的實驗室選擇能源材料作為研究主軸,有太陽能電池和熱電材料,同時團隊也專注研究可還原二氧化碳的光催化材料,以及與燃料電池相關的催化劑。
陳貴賢看好將來能源材料的發展,因為在 2050 淨零排放之前,有愈來愈多企業紛紛加入「RE100 倡議」的行列,企業必須承諾最晚於 2030 年前使用 100% 再生能源。最著名案例是科技巨頭蘋果、Google 和微軟等公司都已宣布其全球供應鏈將符合 RE100 的要求。其中,台積電為蘋果主要供應商,2020 年也加入 RE100,目前為臺灣再生能源的主要買家。
可以預見,將來風能、太陽能與燃料電池的相關材料有其市場需求,而能夠減少二氧化碳的光催化材料,也將成為全球減碳的利器。陳貴賢提到,當前光催化材料還在基礎研究階段,目前的人工光合作用效率約 1%,接近大自然效率,而團隊希望提升到至少 5% 到 10% 以上,方能有其實用價值。
陳貴賢進一步強調,未來效率提高之後,能夠轉化二氧化碳的光催化材料就會有很大的經濟價值,不僅轉化後的燃料可以賣錢,處置二氧化碳原料亦可以收取負碳費用,是一種前所未有的概念。
 陳貴賢強調,未來效率提高之後,能夠轉化二氧化碳的光催化材料就會有很大的經濟價值。
陳貴賢強調,未來效率提高之後,能夠轉化二氧化碳的光催化材料就會有很大的經濟價值。
圖|研之有物
註解
- 根據 IPCC 的資料,如果要將全球暖化幅度控制在 +1.5 °C 以內,必須在 2050 年左右達到二氧化碳的淨零排放目標,同時也要大幅度降低非二氧化碳的溫室氣體排放,特別是甲烷。