黃金比例如何啟發世界的「美」！

本文轉載自諾貝爾化學獎專題系列，原文為《【2011諾貝爾化學獎】具有黃金比例的晶體 — 準晶》

• 譯者／蔡蘊明｜台大化學系名譽教授
• 圖／曹一允｜美國德州農工大學 Karen Wooley 教授指導下取得博士，現於日本萊雅公司進行研究。

十重對稱的黃金比例

當丹尼．謝西曼（Daniel Shechtman）將這個讓他得到 2011 年諾貝爾化學獎的發現登記於實驗記錄簿上時，在後面寫下了三個問號，因為從那些在他眼前的晶體裡面的原子，產生了一個不可能的對稱性，那就好像一個足球——一個球面 ——不可能只由正六邊形組成。從此之後，有趣的馬賽克圖案（Mosaic）、數學裡面的黃金比例以及藝術，幫科學家們解釋了謝西曼那令人困惑的觀察。

「Eyn chaya kazoo」，丹尼．謝西曼用希伯來語告訴自己「不可能有這種東西」。時值 1982 年 4 月 8 號的早晨，他正在研究的物質，是一個由鋁和錳組成的混合物，看起來很奇怪，因此他用電子顯微鏡，企圖從原子的層次來觀察，但是透過電子顯微鏡得到的圖像，卻違反了所有的邏輯：他看到一些同心圓，每一個都是由十個相互等距的亮點所組成（圖 1）。

謝西曼迅速地將灼熱的熔化金屬冷卻下來。這種溫度的突然改變應該會讓原子的排列混亂，但是他所觀察到的圖案，卻說出了一個完全不同的故事：那些原子以一種違反自然定律的方式而排列。謝西曼一再重複地數著那些點，四個或六個點是可能的，但十個是絕不可能。他在實驗記錄簿上寫下：十重對稱？？？

一個未知的發現

為了瞭解謝西曼的實驗結果，以及為何他會如此驚訝，讓我們想像下面的一個課堂實驗：一位物理老師讓光通過一個鑿有縫隙的金屬板，一個被稱為繞射光柵的物體（圖 2），當光波通過這個光柵時，它會產生折射，就好像海浪的波紋通過一個防波堤的開口一般。

在光柵的另一邊，波紋以一個半圓方式散開，並與其它的波紋相交，波峰與波谷相互地加強或減弱。在繞射光柵後面的螢幕上，一種具有明暗的紋路出現，稱為繞射圖紋。

這就是謝西曼在 1982 年 4 月早晨所得到的那種繞射圖紋（圖 1），只不過他的實驗是不同的：他不是用光，而是用電子（註：電子具有波的性質），而他的光柵就是那個快速冷卻了的金屬原子之間的縫隙。

此外，他的實驗是三度空間的，而非平面的。

那個繞射圖紋顯示，在那金屬之內的原子是排列成一個整齊有序的晶體。這當然不意外，幾乎所有的固體物質，不論是冰塊或金子，都具有整齊的晶體。雖然謝西曼使用電子顯微鏡非常有經驗，然而，一個由十個亮點排列成的圓形，卻是過去他從未看到過的。

更有甚者，這樣的晶體並沒有被列在國際晶體規格表之內，那是一個結晶學的主要參考指引。在當時的科學，明訂了一個由十個亮點排列成的圓形圖紋是不可能的，而其證明是非常簡單而明顯的。

違反所有邏輯的圖紋

在一個晶體中，原子是以固定而重複的方式排列的。決定於化學的組成，它們會具有不同的對稱性。在圖 3a 中，我們可以看到每一個原子是由三個原子圍繞著，而形成不斷重複的排列圖案，產生一個三重對稱；將此圖案轉動 120 度，又會得到相同的圖案。

同樣的原理發生在四重對稱（圖 3b）以及六重對稱（圖 3c），圖案不斷重複。當你個別地轉動 90 度或 60 度，相同的圖案會重複出現。

然而，五重對稱（圖 3d）是不可能的，某些原子之間的距離會小於其它原子之間的距離，也就是說，相同的圖案不會重複。科學家認為這足以證明五重對稱不可能存在於晶體中。同樣的原因存在於七重對稱或更高重的對稱。

謝西曼卻發現，他的圖案轉動一個圓的十分之一的角度（36 度）時，又可得到相同的圖案。他的確看到了一個被認為不可能的十重對稱，因此，不意外地，他在實驗記錄簿上寫下了三個問號。

基本假設出錯了

在美國國家標準局（NIST），謝西曼從他的辦公室向外探頭，望了望走廊，希望能看到某一個可以與他分享發現的人，但是走廊空無一人，所以他回到電子顯微鏡前，對那個晶體繼續進一步的實驗。其中他重複地確認所得到的不是巒晶（twin crystal）：兩種共生的晶體享有相同的晶面，而導致了奇怪的繞射圖紋；但是他無法找到任何的跡象顯示那是巒晶。

除此之外，他將電子顯微鏡下的晶體轉動，看看到底要轉多少度可以讓這個十重對稱的繞射圖紋重複出現。實驗顯示晶體的對稱性與圖紋的十重對稱不同，但仍然是一個不可能的五重對稱。謝西曼的結論是：科學界的基本假設是錯誤的。

當謝西曼告訴科學家們他的發現時，他面對了完全的否定，一些同事們甚至認為這根本是無稽之談，許多人宣稱他所得到的是巒晶。實驗室的主管丟給了他一本結晶學教科書，建議他讀讀。謝西曼當然知道教科書裡面說了什麼，但是他更相信自己的實驗。

根據謝西曼的回憶，所有的騷動終於導致他的老闆要求他離開那個研究小組，狀況變得非常難堪。

與已知奮戰

謝西曼是在以色列科技大學（Technion-Israel Institute of Technology）修得博士學位的。在 1983 年，他引發了在他母校任職的伊蘭．布雷契（Ilan Blech）對這個研究的興趣，他們合力企圖解釋此一繞射圖紋，並轉譯成為原子在晶體內的排列模式。

於 1984 年夏，他們送了一份論文稿到應用物理期刊（Journal of Applied Physics），但是該稿似乎在收到當日，就即刻被編輯退回。

接著，謝西曼向約翰．康（John Cahn）提出要求。康是一位著名的物理學家，也是當初邀聘謝西曼到 NIST 的人。謝西曼希望康能看看他的數據。這位通常很忙的學者終於答應，接著，康與一位法國的結晶學家丹尼斯．格拉提亞斯（Denis Gratias）諮詢，看看謝西曼是否忽略了什麼，但是根據格拉提亞斯的檢驗，謝西曼的實驗是可以信賴的，格拉提亞斯如果親自做那些實驗，也會使用同樣的方法。

在 1984 年的十一月，偕同了康、布雷契與格拉提亞斯，謝西曼等人終於在 Physical Review Letters 這份期刊中，共同發表了他的數據。這篇論文像顆炸彈一般，投在結晶學者之間。它質疑了他們的科學學門中的最基本教條：所有的晶體具有重複的週期性結構模式。

揭開知識的迷障

現在這項發現觸及了更多的讀者，而謝西曼成為了更多批評的目標。不過，在此同時，全世界的結晶學者們都產生了一種似曾相識的感覺，許多人在分析一些其它的物質時，也曾經得到過類似的繞射圖紋，但是當初，他們都將之視為巒晶的證據。現在，他們開始翻箱倒櫃，找出以前的實驗記錄簿，很快發現有些其它的晶體也會產生這種看似不可能的圖紋，譬如八重和十二重的對稱。

在謝西曼發表了他的發現之後，他仍然不知道那個奇怪的晶體內部結構到底如何。顯然地，它的對稱性是五重的，那是何種堆疊方式呢？這個答案卻從另一個未曾料到的領域而得：數學中的馬賽克遊戲。

用以解謎的馬賽克

數學家們喜歡用迷團和邏輯問題來挑戰自我。於 1960 年代，他們開始思索是否可以用有限數目的圖案塊，舖出不會重複的馬賽克圖案，創造一種所謂的「非週期馬賽克」。

頭一個成功的嘗試是在 1966 年，由一位美國的數學家所發表，但是他需要超過兩萬種圖案塊來做到，這很難讓著迷於精簡的數學家滿足。當更多的數學家投入這項挑戰，需要的不同圖案塊數目穩定下修。

終於，在 1970 年代中期，一位英國數學教授羅傑．潘洛斯（Roger Penrose）對此問題提出了一個最漂亮的解答。他用僅僅兩種圖案塊創造出非週期馬賽克，例如一胖一瘦的菱形（圖 4-1）。

潘洛斯的馬賽克在好幾個不同方面啟發了學界，其中之一是他的發現被用來分析中世紀伊斯蘭綺理（Girih）圖案。我們也發現阿拉伯藝術家早在 13 世紀就創造出了非週期馬賽克，這種馬賽克裝飾著非凡的西班牙阿罕布拉宮，還有伊朗 Darb-i Imam 寺廟的入口和穹頂。

結晶學者艾倫．馬凱（Alan Mackay）運用潘洛斯的馬賽克於另一個方面，他想探究構成物質的原子是否也能如同非週期馬賽克的圖案般排列。他做了一個實驗，用代表原子的圓圈放置在潘洛斯的馬賽克圖案的交點位置（圖 4-2），然後用這樣的圖案作成繞射光柵，來看會得到何種繞射圖案，結果得到一個十重對稱——十個光點圍成一圈。

馬凱的模型與謝西曼的繞射圖紋之間的關聯性，接著被物理學家保羅．史坦哈特（Paul Steinhardt）與多夫．李凡（Dov Levine）所發現。謝西曼的論文在 Physical Review Letters 這份期刊上發表之前，編輯將該文稿交由其他的科學家審核，在這個過程中，史坦哈特有機會看到這份文章，他早就對馬凱的模型熟悉，因此體認到馬凱的理論模型，存在現實世界中，亦存在於謝西曼在 NIST 的實驗室裡。

在 1984 年的聖誕夜，就在謝西曼的論文出刊後的四週，史坦哈特與李凡發表了一篇論文，其中描述了準晶體（quasicrystal）以及它的非週期馬賽克排列。在這篇論文中，準晶體得到了它的名字。

關鍵的黃金比例

準晶體與非週期馬賽克具有一項共同的迷人特質，那是一個在數學與藝術中不斷出現的黃金比例，亦即數學常數 tau。例如：在潘洛斯的馬賽克中，胖的和瘦的菱形數目的比例是 tau；類似地，準晶體中原子間的不同距離的比例，總是與 tau 相關。

13 世紀的義大利數學家費布那西（Fibonacci），從一個有關兔子繁殖的假設性實驗中找到的一系列數字中，描述了這個數學常數 tau。在這個著名的數列中，每一個數字是前兩個數字之和：1、1、2、3、5、8、13、21、34、55、89、144 等等。如果將一個費氏數列中較大的數字除以前一個數字，例如 144/89，你就會得到一個接近黃金比例的數字。

當科學家想要用一個繞射圖紋來描述準晶體中的原子排列時，費氏數列與黃金比例對他們是很重要的。費氏數列也可以解釋 2011 年的諾貝爾化學獎所表彰的發現，為何改變了化學家對晶體結構的規律性之看法。

不會重複的規律

先前，化學家解釋晶體的規律性在於一個週期性不斷重複的模式。費氏數列雖然不會重複，卻也是規律的，因為它遵守一個數學的規則。

在準晶體中，原子間的距離與費氏數列相關，原子以規律的方式排列，化學家可以預測一個準晶體中的結構是何樣，不過這種規律性與具有周期性結構的晶體是不同的。

在 1992 年，這個認知導致了國際結晶學會改變了他們對晶體的定義。先前對晶體的定義是「一個物質，其中組成的原子、分子或離子以一個整齊而且重複的方式堆疊成立體的型態」，現在新的定義是「任何固體，基本上具有可區別的繞射圖紋」，這個定義比較寬廣，而且允許未來可能發現的其它種晶體。

準晶體也存在於…

從他們 1982 年的發現之後，數以百計的準晶體在全球許多實驗室中被合成，但一直到了 2009 年的夏天，科學家才第一次報導了天然的準晶體。他們發現了一種採自東俄的哈吐卡（Khatyrka）河的樣本中之礦石。這種礦石是由鋁、銅和鐵組成，具有一個十重對稱的繞射圖紋。它被稱為二十面石（icosahedrite），此名源自於二十面體（icosahedron），那是一種具有 20 個正三角形面的幾何固體，黃金比例存在於其幾何結構中。

準晶體也被發現存在於一種世界上最耐用的鐵當中。在嘗試不同組合的金屬時，一家瑞典的公司成功的製備出一種鐵，具有許多令人驚訝的良好特質。分析它的原子排列結構時，顯示它具有兩種相：硬鐵的準晶體嵌在一種較軟的鐵中，此一準晶體具有一種盔甲的功能。現在它被用於刮鬍刀片，以及眼睛手術的細針等產品中。

除了特別堅硬外，準晶體能像玻璃般輕易的碎裂。

由於其特殊原子排列結構，它們也是很差的熱與電的導體，以及含有不具黏性的表面。其低熱傳導的性質可以讓它們成為有用的熱電材料，能將熱轉為電，發展這種材料的目的在解決熱能的再利用，例如用在汽車與卡車上。現在科學家們正在實驗將準晶體用做像是煎鍋，以及節能的發光二極體（LED）之表面塗料，或是作為引擎的隔熱等等。

保持開放的心

謝西曼的故事並非唯一。

在科學的歷史中，一再地有研究工作者被迫與已經建立的「真理」作戰。事後看來，那些真理不過是一些假設。謝西曼和他的準晶體所面對過的最嚴厲批評，來自於鮑林（Linus Pauling），他曾得過兩次諾貝爾獎。這很清楚地顯示，即使是我們最偉大的科學家，也無法免疫於被陷在舊教條當中。

保持一個開放的心態，勇於質疑已經建立的知識，實際上可能是科學家們最重要的性格特質。

參考資料

• 本文譯自諾貝爾化學獎委員會公佈給大眾的新聞稿：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/info_publ_eng_2011.pdf
• 若需要進一步的資訊，請至以下網頁點選：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/sciback_2011.pdf

• 作者：王浤齡、陳玟蓉、高珮珊／台北市立大同高級中學

「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後，一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習，運用數學知識，培養及展現邏輯思考與文字撰寫的能力，盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2021 數感盃青少年寫作競賽／高中組專題報導類佳作之作品，為盡量完整呈現學生之作品樣貌，本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

在拍照時，我們總是希望能夠自然地呈現出最漂亮的自己，但這是一件何其困難的事情。法國傳奇攝影師——羅伯特・杜瓦諾曾說：「如果我知道如何拍出好照片，那我每次都會拍出好照片了。」然而有沒有什麼拍攝方法，可以讓照片中的身材比例變得更完美呢？ 

有一天，我和一群朋友到某間知名服飾店逛街，試穿今年流行的秋冬款，並拍照片比較看看，選出較適合自己的衣服。在過程中，我發現一個問題：「為什麼在店家試穿時，全身鏡映照出的自己總是比照片中好看？」

嘗試幾次後，我們發現這是因為自己的身材比例，在鏡子與照片中的呈現是不一樣的，服飾店內的全身鏡，總是使腿的比例看起來比較長。

於是我們開始好奇，拍照時要如何拍攝出如同店裡的全身鏡具有長腿效果的方法，以及，是什麼原因讓這間服飾店內的全身鏡會有這樣長腿的效果呢？ 

上網搜尋之後，發現在這個社群軟體發達的時代，網路上有許多人分享不用俢圖軟體，就能「拍」出完美比例的文章或是教學影片，其結論是：「把手機或相機傾斜一個角度，就可以讓人的腿在照片中的比例變長。」然而，所謂的「傾斜一個角度」到底是幾度，卻沒有網站提供。

事實上，每個人身高比例皆不相同，取景的遠近都不一樣，甚至使用的拍攝器材也不 盡相同，使這個「角度」也會因情況而有所不同。因此，我們試著用所學的數學工具，去推論出不同人在拍照時，手機應該要傾斜幾度才能達到想要的長腿效果？ 

關於服飾店內全身鏡有長腿效果的原因，我在觀察這些鏡子後，發現它們都有傾斜（如圖一），而且與地面都是夾 80 度。這個傾斜角度到底有什麼樣的用意呢？我們試圖去解開這個業界沒有說出來的秘密。 

首先，我們先解釋物理上的「成像原理」。人的眼睛之所以能看到物體、相機可以拍到畫面，都是因為物體反射的光線，進入到眼睛內的視網膜、或是相機裡的底片後所成的「像」。

成像的原理與國中理化所教的凸透鏡成像原理相同，是由三條光線所交會而成的像（圖二），其中平行光通過透鏡後會穿過焦點，而穿過焦點的光通過透鏡後會成為平行光，交會處就是成像地點；並且第三條穿過透鏡的直線光也會與前兩條相交，因此可以由物距與像距算出成像縮放的倍率。 

如果我們在成像位置放一個平面，當成像的平面與物體是平行時，像會與實物相似，但是上下顛倒；但是如果把成像平面傾斜一個角度的話，成像的比例就會因為傾斜的角度，而 與實物的原比例不同。 

我們想要研究相機傾斜角度對照片中人物的身材比例的影響。 

考慮拍攝時，相機高度與被拍攝者的肚臍位置相同，如上面圖三所示，點 D 為相機的焦點，物體反射的光線直線穿過 D點，在另一側的平面上呈現一個倒立的像。

把 \( \overline{AC} \) 當成為一位站立著的被拍攝者， \( \overline{AB} \) =b 為被拍攝者的頭頂到肚臍的長度，即為身長；而 \( \overline{BC} \) =l 為被拍攝者的肚臍到腳底的長度，即為腿長； \( \overline{BD} \) =d 為被拍攝者與相機的距離。

當成像平面垂直地面時，若把像距等比例放大到等於物距時（即是 \( \overline{DI} \) =d ），則 \( \overline{HJ} \) 會是一個全等的倒立像，即 \( \overline{HI} \) =l 為像的腿長、 \( \overline{IJ} \) =b 為像的身長。

若把成像平面傾斜一個角度，轉成 \( \overline{EJ} \) ， 則像的身長會被拉成 \( \overline{IJ} \) → \( \overline{FJ} \)  ，像的腿長會被拉成 \( \overline{IH} \) → \( \overline{FE} \) 。

接下來，我們將推導出一條公式，可以算出相機該傾斜幾度，才能讓被拍攝者的身長及腿長呈現我們所想要的比例。 

假設在照片中，身長比腿長的比例為 \( \overline{FJ} \) : \( \overline{EF} \) =1 : r，先求出 \( \overline{HD} \) : \( \overline{HE} \) 。

如圖四，我們利用「孟氏定理」， ΔJEH 被直線 \( \overline{FD} \) 所截的線段比為

 \( \frac{\overline{JI}}{\overline{IH}} \) ✕ \( \frac{\overline{HD}}{\overline{DE}} \) ✕ \( \frac{\overline{EF}}{\overline{FJ}} \) =1  \( \Rightarrow \) \( \frac{b}{l} \) ✕ \( \frac{\overline{HD}}{\overline{DE}} \) ✕ \( \frac{r}{1} \) =1，則 \( \frac{\overline{HD}}{\overline{DE}} \) = \( \frac{l}{br} \) 。

又因為圖三中， \( \overline{IH} \) // \( \overline{EG} \) ，所以 \( \frac{l}{br} \) = \( \frac{\overline{HD}}{\overline{DE}} \) =  \( \frac{\overline{DI}}{\overline{DG}} \) = \( \frac{d}{\overline{DG}} \)  \( \Rightarrow \)  \( \overline{DG} \) = \( \frac{bdr}{l} \)

\( \overline{IG} \) = \( \overline{DG} \) – \( \overline{DI} \) = \( \frac{bdr}{l} \) -d

因為 ΔEFG ≈ ΔJFI，所以  \( \frac{\overline{IF}}{\overline{FG}} \) =  \( \frac{\overline{FJ}}{\overline{EF}} \) =  \( \frac{1}{r} \) ；可推得：

\( \overline{IF} \) = \( \frac{1}{(1+r)} \) ✕ \( \overline{IG} \) = \( \frac{1}{(1+r)} \) ✕  \( \left ( \frac{bdr}{l}-d \right ) \)

因此，若相機傾斜的斜率為 m，則

從這個公式可知，我們只要知道以下數據，代入公式之中即可算出相機的斜率：

若圖中 \( \overline{AJ} \) 的斜率與 \( \overline{CH} \) （原文使用的是雙箭頭線段符號，但公式表中找不到，所以就先以線段符號代替）的斜率分別令成 m_b 與 m_l ，則相機傾斜的斜率公式可用斜率簡化表示為

我們根據此公式進行以下實作。 

拍攝工具為 iPhone 手機，被拍攝同學的身體數據如下表一： 

我們設定畫面高度與人物身高的比例黃金比例（約為 1：0.618），而由〈物距計算器〉網站，可算出此畫面下的拍攝距離為 144.7 公分。並且，我們希望拍攝出的身長與腿長也是黃金比 例，即  \( r=\frac{1}{0.618}=1.618 \)。

由表一，因為 m_b = －身高 / 物距 =  \( \frac{-67.5}{144.7} \)，m_l = 腿長 / 物距 =  \( \frac{95.5}{144.7} \)，所以帶入公式可得：

因此，拍攝時手機傾斜的斜率約為 8.538，換算成角度： 

所以手機在拍攝這位同學時應該要傾斜 83.3°。

下圖是手機傾斜前後拍照出來的照片效果對比： 

從右圖看得出來，照片中的腿部確實有拉長的效果，其比例為 1 : 1.84，但並非是當初我們給 定的黃金比例。這個原因是來自於 iPhone 手機鏡頭視角的限制，當手機傾斜時，放在腰部的高度，被拍者會無法全身入鏡。所以，我們將手機高度降低至能夠完全拍攝到整個人，因而導致加大拉長效果。

因此，我們建議在拍攝時，若需要降低手機高度，則手機與地面夾角，要比原計算出來的角度更接近 90° 一點。 

接下來，我們利用研究的結果去計算，各個年齡層與性別的人在拍照時，身長與腿長在照片中要呈現黃金比例，手機適當的傾斜角度分別為幾度。

下圖五，是內政部〈建築使用行為與本土人因工程關連性研究〉指出的 19 項人體計測尺寸中的部份數據；而下圖六，則是將圖表的數據進行以下的計算，去推論一般人平均的身長與腿長。

• 膝蓋高度 − 膝膕高度 = 大腿厚度 
• 坐高 − 大腿厚度 = 身長（頭頂到肚臍） 
• 身高 − 身長 = 腿長 

把各個年齡層與性別的平均身長與腿長整理成下表二。最後，我們各別將數據代入公式計算得出，不同人在拍照時，手機的傾斜角度，如下表三所示。 

表格三中，65 歲以上的民眾要拍出黃金比例的手機角度比較垂直，是因為數據的統計有將駝背也考慮進去，導致統計出的結果，相對其它年齡層來說腿的比例較長。但普遍來說， 在未滿 65 歲的各個年齡層拍照時，手機傾斜角度分布在 65 ~ 70° 之間。

然而，考慮到手機傾斜時又要全身入鏡，需要降低手機拍攝的高度，會更加拉大腿長的比例，因此，一般人在拍照時，若想讓身長比腿長接近黃金比例的話，我們建議：

服飾業內不能說的秘密，全身鏡傾斜 80° 的原因！

在前文中，我們想探討第二個問題，是服飾店的全身鏡為什麼都與地面夾 80°。其斜置的原因，明顯是要讓腿看起比較長，但為何不用其它的角度而恰好是 80° 呢？ 

斜鏡面會產生仰視效果，讓人感覺鏡中的人像向後仰，使腿的視覺效果變長。事實上， 長腿效果與我們研究的主題一致，同樣是實物（鏡中後仰的人像）與成像平面（視網膜）不平行，因此後仰角度與視覺比例的關係，符合前文推論的公式。

如下圖七所示，全身鏡傾斜 80° 後，由於鏡子和直立的人夾角 O 為 10°，因為鏡射原理，鏡子和像的夾角也為為10°， 所以像會傾斜 70°，且 ∠ACD = ∠AOB = 10° 。

實際到店家測量全身鏡前的走道寬度，約為 78 公分。也就是一般民眾會站在距離約 78 公分的位置使用全身鏡，即 \( \overline{DE} \) = 78，則 

78+ \( \overline{EC} \) = \( \overline{DC} \) = \( \overline{AC} \) cos(10º)

 \( \Rightarrow \) 78+ \( \overline{EC} \) = 2 \( \overline{BC} \) cos(10º)

 \( \Rightarrow \) 78+ \( \overline{EC} \) = 2 \( \overline{EC} \) cos(10º)

因此，可以算出 \( \overline{EC}=\frac{78}{2cos^{2}(10^{\circ})-1}\approx 83 \)

所以當我們照鏡子時，眼睛與成像的距離為 78+83=161 公分。若成年女性（平均身長 75.6 公分、 腿長 81.8 公分）使用服飾店的全身鏡時，看到鏡中自己的比例（腿長 / 身長）為 r，則

 \( \frac{(1+r)\times \left ( -\frac{75.6}{161} \right )\times \left ( \frac{81.8}{161} \right )}{r\times \left ( -\frac{75.6}{161} \right )+\left ( \frac{81.8}{161} \right )}=tan(70^{\circ})\approx 2.747 \)

 \( \Rightarrow \) r ✕ [(-0.4696) ✕ 0.5081+2.747 ✕ 0.4696] = 0.4696 ✕ 0.5081 + 2.747 ✕ 0.5081

 \( \Rightarrow r=\frac{0.4696\times 0.5081 + 2.747\times 0.5081}{ [(-0.4696)\times 0.5081+2.747\times 0.4696] }=\frac{1.63435446}{1.0.5138744}\approx 1.565 \)

這個結果非常接近黃金比例。

用其它年齡層與性別的數據去計算，也可得到 r ≈ 1.618 ± 0.05

因此，我們發現服飾店會在店內全身鏡會斜置 80° 的原因，很可能是因為要讓顧客認為穿上自家的衣服後，會讓比例接近於黃金比例，以提升購買慾望。

結合我們計算的數據和實作的結果，可以得出一些結論：大多數的人拍攝時，如果想要拍出身體的比例接近黃金比例，手機需要傾斜的角度大約為 65° ~ 70°。若將傾斜時，可能會把手機高度降低的因素考慮進去，則是以 70° 為最佳角度。

下次拍照時，不妨也將手機傾斜成 70°，或許會有意想不到的效果！

參考資料

• 均一教育平台
• 內政部建築研究所研究報告
• 物距計算機 

• 作者／大衛．翁弗拉許；譯者／林柏宏

科學的起源：以真實性質的角度來理解自然

二十世紀物理學家理查． 費曼（Richard Feynman，1918-1988）認為，當代物理學奠基於巴比倫人的數學方法，他們會以數學的方式來闡述問題，這種經驗能夠讓人學會歸納，進而發現自然原理。歐幾里得（Euclid ofAlexandria，西元前三世紀中期到西元前 285 年）的治學方法則與此相對，這位希臘思想家運用基本的邏輯規則，從我們稱為公設的基礎事實推導出更多複雜的定理。

在大約西元前三百年時，歐幾里得的方法很流行，而他的演繹法發源於更早的幾世紀前，當時的希臘思想家剛開始大膽地以真實性質的角度來理解自然。

對於月亮、太陽與眾行星性質的了解要真正有所進展，希臘的天文學家就得接受量化的方法。他們會需要巴比倫人研究天文的方法，包含實際數學運算，以及從單調的天象觀測中蒐集大量資料。他們的研究必須將這些資料融合希臘文化特有的、探討本質的思維。這種思維是從西元前六世紀的愛奧尼亞人社群開始的。

愛奧尼亞地區位於今日土耳其西部沿岸的城市與島嶼，最早開始推斷大自然是可探究、可預測的希臘人都來自這一帶，他們認為大自然的運作與眾神的意志無關。這種去除神祕面紗的世界觀由米利都的泰利斯起頭，從而解放了愛奧尼亞人的思考，開始為自然現象提出物理學的解釋模型，對科學的進步發揮了重要作用。

然而，希臘世界另一邊的哲學家都反對泰利斯的論點，這些哲學家的根據地是位於南義大利的希臘殖民地─大希臘（Magna Grecia）。

在這場論爭裡，一些大希臘區的哲學家其實是最早發現月亮是球形而非一圓盤的人，有一批大希臘的人還引進了會讓希臘天文學突飛猛進的數學知識。但是，大希臘區並無科學思維，這裡的人高張神祕主義，鄙視實證精神，影響力最大的神祕主義團體還掩蓋、打壓與其主張相左的新發現。

諷刺的是，這個神祕主義勢力團體的創始人，出生於愛奧尼亞區中心地帶薩摩斯島（Samos）的畢達哥拉斯（Pythagoras，約西元前 570-495），其實就學於泰利斯門下，並由此展開他的學術之路。

泰利斯預測日食，阻止戰爭

要是西元前二千六百年就有諾貝爾和平獎，肯定會頒發給米利都的泰利斯。

他出生時，正是巴比倫文明崛起，催生出前所未有的知識創發活躍期，他也漸漸愛上數學與天文學。愛奧尼亞隸屬於呂底亞王國（Lydian），不過泰利斯或許去過巴比倫，不然就是取得了巴比倫的天文學文獻。不管是哪種情形，泰利斯都認識到日食與月食的沙羅週期，這與他的想法不謀而合，他本來就認為神明與自然無涉。

當時呂底亞正與其敵對國之一，米迪亞（Media）交戰，泰利斯知道雙方指揮官都是迷信的人，便提出警告說，眾神要求他們休兵，並且會在西元前五百八十五年春季的某一天使太陽暗下來，以表明神意，其實泰利斯根據沙羅週期進行計算後，已經得知這一天應該會發生日食。

儘管泰利斯自己未察覺，但當他如此運用沙羅週期時，實際上計算的正是月球在太陽前方的移動。總之，日食確實出現了，戰事也平息了，泰利斯在愛奧尼亞聲名大噪，想向他學習自然研究的人蜂擁而至，其中一位就是從薩摩斯島搭船前來的畢達哥拉斯。

當時的米利都是個富庶的港口城市，當地的希臘居民不願向帝國統治者效忠，他們獨立自主，擁抱新知，或許是因為常從各地的航海貿易商口中得知新觀念，長此以往，泰利斯與其他米利都人的思考方式開始變得新穎激進。

比方說，他們認為地震是由於海中巨浪擊打陸地，土地陸塊是來自海水淤積堆造而成。這些關於自然的解釋終究會被證明並不正確，但重要的是，當時他們的想法和其他地方的人不一樣，他們的想法是可以接受驗證、有可能被否證推翻的，與那些虛無縹緲的神明無關。

泰利斯和在他之後的愛奧尼亞人之所以與眾不同，乃在於他們斷定，認識自然是可行的，可以接受觀察與分析─ 而且，對於他們之中某些人而言，也能透過試驗實證。

為封口無理數的發現而殺人的畢達哥拉斯

薩摩斯的畢達哥拉斯是目前已知世上最早指出月亮是球狀的第一人，他會這麼想或許一開始源自觀察的結果，例如發現月球明暗分界線（lunarterminator）是彎曲的，這道線區分了月球被照亮與未被照亮的兩部分。

畢達哥拉斯畢竟是泰利斯的學生，而且比同時代的人更早認出晨星（the MorningStar）與暮星（the Evening Star）是同一顆物體─ 金星。這種認知來自於觀察，雖然畢達哥拉斯後來排斥觀測，轉而堅持藉由純粹的思索即可了解宇宙。

旅居埃及多年，又去了巴比倫之後，畢達哥拉斯帶來了一項定理，直角三角形斜邊圍成的正方形面積，等於兩短邊各自圍成正方形的面積和。這不是他自己想出來的，埃及人與巴比倫人早將這觀念實際運用在生活中好幾百年了，巴比倫甚至發展出三角學這門數學。無論如何，由於畢達哥拉斯將這個定理引介給希臘人，未來幾世代探究大自然所需的數學知識才有機會出現。

但對畢達哥拉斯而言，數學不僅是工具，而是宗教信仰。

球狀月亮的想法只是畢達哥拉斯兄弟會神祕思想的一部分，畢達哥拉斯在位於義大利的克羅敦殖民地（the Croton colony）創立了這支教派。畢達哥拉斯教徒主張天界的「星球和諧」，認為月亮與其他星體不只是球形，而且是完美球形，繞著絕對的圓旋轉，每顆星球會產生特定的音符。再加上畢達哥拉斯輕視觀測法，凡是和其完美和諧觀念牴觸的新發現都一貫打壓。

其中一例是他的學生發現數字 2 開平方根會得到無理數，也就是無法化作分數，不能以兩個整數做為分子與分母來表示。謠傳畢達哥拉斯為了封口，謀殺了那個學生。

但他並不需要依靠暴力來提倡自己的學說。不久後，柏拉圖（Plato，約西元前 427-347）將熱心採納畢達哥拉斯的神祕主義，包含那些完美球形、圓形軌道、對觀察實測的輕蔑，以及阻撓接下來幾世紀科學進展的一切花俏玩意兒。

採納實證主義的亞里斯多德

和他的老師柏拉圖比起來，亞里斯多德比較有科學精神。

雖然兩人的出發點都是想將畢達哥拉斯、巴門尼德提倡的這類神祕主義哲學與愛奧尼亞人的自然主義整合在一起，柏拉圖終究傾向了神祕主義，亞里斯多德則對愛奧尼亞思維更有好感。若提到愛奧尼亞的實證主義（empiricism）── 主張知識必須透過感官作用的經驗才能取得，兩人的分歧會特別明顯。

愛奧尼亞人泰利斯觀察尼羅河的沉積土層後，做出了假設，認為全世界的大塊陸地都是經由類似過程，從一原始大洋中形成的。而泰利斯的學生、米利都的阿那克西曼德（Anaximander of Miletus，西元前 610-545）觀察幼魚和人類的差異，並在看過化石骨骼後，構想出早期版本的生物演化假說。綜合他們的所見所聞，愛奧尼亞人了解到，大自然不停地在變動。

亞里斯多德在研究如生物這一類地球上的物質時，大致上採納愛奧尼亞式的實證主義與變化觀念，可是一旦主題來到天象，他就表現出神祕主義的遺緒。畢達哥拉斯有個很妙的想法，認為天上的星體都是繞著正圓形軌道轉的完美球形，亞里斯多德深受此思想荼毒，同時還採用巴門尼德的主張，認為萬物恆定不變，結果形成了以下觀點：

星星、太陽與行星都是恆久不變的，有永遠固定的幾何形狀，地球是墮落不潔的，也因此不完美。違背這完美理念的還有月球表面的暗黑地貌，亞里斯多德對此的解釋是，月球和地球走太近了，太靠近存在於地表上的汙染，指的就是人類和其他生命形式。

——本文摘自《月球之書》，2019 年 9 月，時報出版。

本文由 微星科技 委託，泛科學企劃執行。

• 作者 / 曾繁安

人類總會不由自主地被閃閃發光的事物吸引，取名時加上「黃金」二字，好像就能讓身價大漲，變得受歡迎。不管是黃金海岸、黃金地段、黃金右腳、 黃金奇異果，黃金獵犬、黃金脆薯、黃金盔甲、黃金流沙包、黃金開口笑（大誤）……人們用黃金形容所有美好的事物，連「比例」也一樣。「黃金比例」被譽為最美好的比例，你一定聽聞過，如果人的臉蛋身體或畫作構圖越接近黃金比例，就越迷人的説法。然而一個數字比例，怎麼會和美學扯上關係？

人類探究黃金比例的歷史，可追溯至兩千多年前……

古希臘時代大約公元五百多年前，癡迷於數學的畢達哥拉斯，認爲數學可以解釋世上一切事物。他的教學吸引了一群熱心的追隨者，被稱爲畢氏學派。在旁人眼裏，畢氏學派恐怕是一群怪人：恪守極爲嚴格的生活條規，不可吃肉和豆類，還會進行高强度記憶力訓練和三省吾身等等。但畢氏學派對數學幾近狂熱崇拜，尤其對數字 5 和五角星形的迷戀，使他們成爲史上最早接觸黃金比例分割的一群人。將構成五角星形的線段分割，由短至長排列，把最短的兩條線段相加，恰恰等於第三條線段長；把第二短和第三短的線段相加，也會等於第四條線段，依序如是，顯示出黃金比例的奇妙！不過，他們並沒有進一步為這個神奇的發現加以解釋、定義和命名。

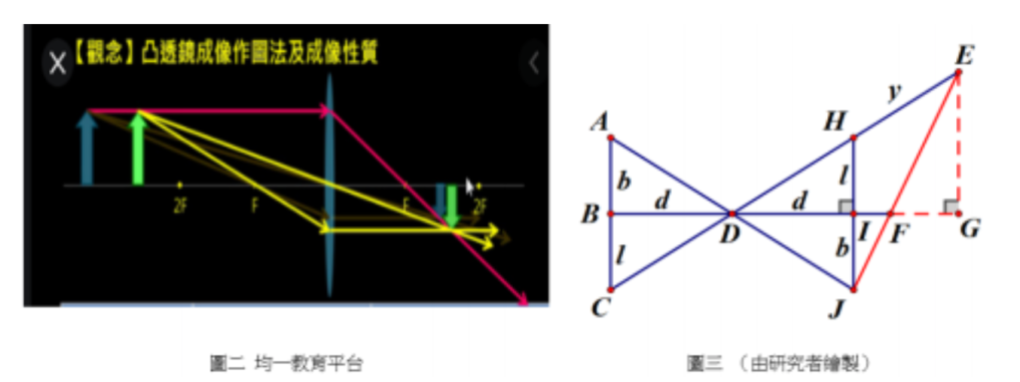
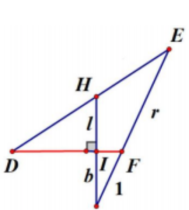
一直到公元前三百年，歐基里德所著的《幾何原本》問世，才有了對黃金比例最早的系統性論述。但你知道嗎？歐基里德也根本沒說過「黃金比例」一詞。後世所謂的「黃金比例」，其實是出現在《幾何原本》第四章的「極限與均值比例」（Extreme and mean ratio）。歐基里德對這個比例的說明如下：

“A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”

（一條線段如果切在「極限與均值比例」上，則線段的全長與較長分割段的長度比例，和較長分割段與較短分割段的長度比例相等。）

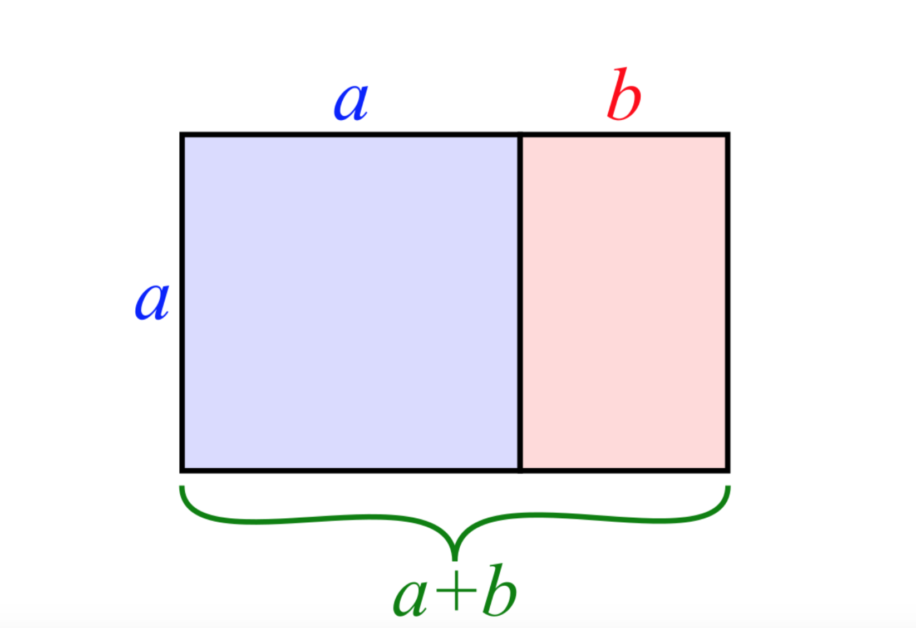
大家常常挂在嘴邊的黃金長寬比 1.618 ，就是從上圖的比例計算而來。只要把較短的線段 b 定義成 1 個單位，較長的線段 a 定義成 x 單位，再用一點國中數學上過的一元二次方程式，就能算出解答為 1.6180339887…… 或 0.6180339887…… 這兩個看～～～不到盡頭的無理數，都可被視爲黃金比例之值。就像另一位大名鼎鼎的無理數——圓周率，是以 「π」來表示，黃金比例也有自己的符號，叫做「φ」。「φ」一般念作 “ fai ” ，跟「π」押同韻，但捍衛正統希臘文念法的人可能會堅持念作 “ fee ”。

當初歐基里德只説了這麽多，純粹是為了解釋數學幾何上的意義。但他想也想不到的是，這個「極限與均值比例」，會變成美的代言人，帶給未來人類無限遐想的空間。

數學與人文藝術匯集，文藝復興時期的「神聖比例」

現代人熟知的「黃金比例」一詞，一直到 1830 年代左右才被廣爲流傳。在此之前，它的地位曾被提升到更崇高、神聖的位置。文藝復興時期，被稱為「會計學之父」的數學家兼方濟會修士——盧卡．帕西奧利（Luca Pacioli），出版了名叫《神聖比例》（Divina scalee）的著作。他從歐基里德定義的「極限與均值比例」出發，對正多面體和半正多面體的性質做討論。

帕西奧利在研究「極限與均值比例」時深受啟發，開始與他熟悉的神學進行連結。他發現這個比例中提到的三個線段（全長、長邊、短邊），都在描述同一條線，像極了基督教的神學觀，既聖父、聖子和聖靈是三位一體。而這個比值之解的無理數，所具備無法窮盡的性質，就如同凡人無法理解全能無限的上帝般，兩個線段之比例是相等的（全：長 = 長：短），則代表神永恆的不變性與無所不在的屬性。

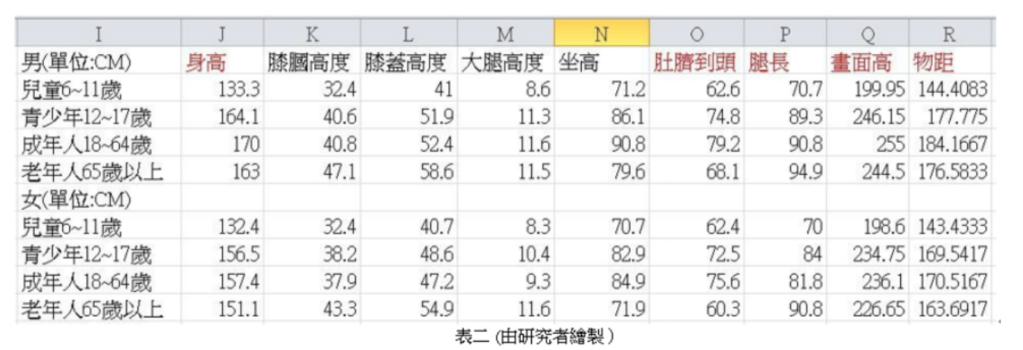
從數學上看見神學解釋的帕西奧利，遂將「極限與均值比例」改稱為「神聖比例」。他在著作中進一步以「神聖比例」分析古希臘羅馬建築與人體結構的比例。在他看來，被神所創造的人類，其軀幹比例也隱含了「神聖比例」。這些內容更深地加強了「神聖比例」與「美」之間的連接。

此後，「神聖比例」便與「宗教」和「美」脫離不了關係。帕西奧利對純數學理論進行宗教哲學解讀的突破，成功地讓這個神奇的比例跨出數學界的舒適圈，成為數學家、神學家與藝術家之間共同的話題，後來更在討論中逐漸演變成後世蔚為流行的「黃金比例」。帕西奧利可説是打開「黃金比例」知名度，背後不可或缺的功臣。

宇宙誕生以來就存在？藏在大自然中的密碼竟是「黃金數列」

儘管吉薩金字塔和帕特農神殿是否依照黃金比例建造，數學界和藝術界還在爭辯不休，但實際上不需要人爲設計，大自然本身就蘊藏著黃金比例的美麗。以描述「兔子生兔子」問題而聞名的費波那契數列（Fibonacci number），可説是黃金比例的孿生手足。費波那契數列第零項是 0，第一項是 1，從第二項以後的值，就是前兩項加起來的和，所以依序會是：

1、1、2、3、5、8、13、21、34、55、89、144、233……

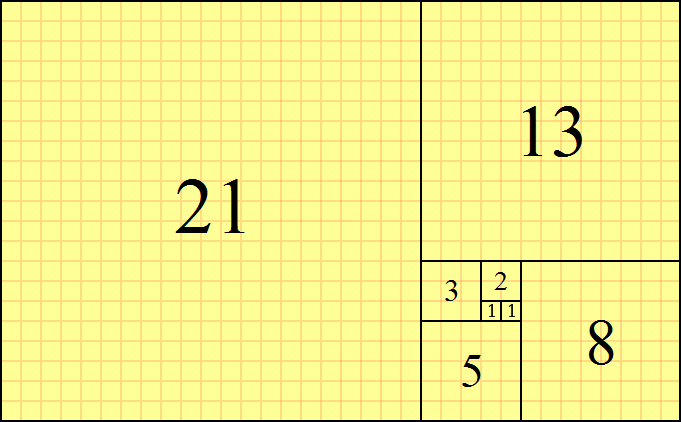
文藝復興後期鼎鼎大名的天文學家克卜勒（Johannes Kepler）發現，把費波那契數列的後一項除以前一項的值的話，會是 1 / 1 = 1， 2 / 1 = 2，3 / 2 = 1.5，5 / 3 = 1.67， 8 / 5 = 1.6， 13 / 8 = 1.625， 21 / 13 = 1.615…… 計算到這裏，你是不是也察覺到其中奧妙？隨著數列遞進繼續相除，這個值竟會越來越趨近於黃金比例！也因此，費波那契數列的別名就叫做「黃金數列」。

大自然中的植物，其實都是深諳造物奧義的數學大師。試著數一數雛菊的花瓣數量，你會發現它們恰好都是 13、21 或 34 的費波那契數。葉子與葉子之間要怎麽喬位子，才不會擋住彼此吸收陽光？玫瑰的花瓣要如何排列，才會顯得漂亮對稱？松果上的種子要怎麽生長，才可以有效利用有限的空間？這些問題的答案通通都是：旋轉角度的比值（以 360° 為分母）要符合黃金比例！

不只是植物界，無論是鸚鵡螺貝殼的生長、鷹隼迫近獵物的飛行軌線，抑或衛星圖上熱帶氣旋的外觀，就連宇宙中漩渦星系的旋臂，都呈現遵循黃金比例的螺線。從小至可一手掌握的貝殼，大至遙遠光年之外的星系，都藏著黃金比例的身影。大自然對這個奇妙比值的鍾愛，讓科學家着迷不已。

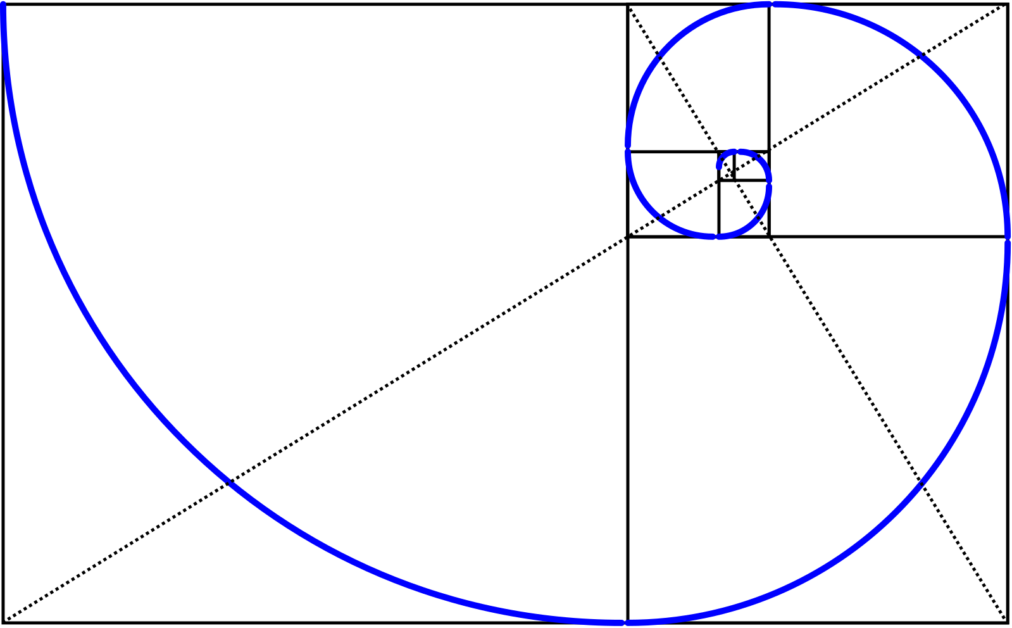
有生命的動植物和無生命的氣旋或星系，都不約而同服膺於一個神奇的比值，展現一種似乎自世界誕生以來就存在，難以撼動、一致而規律的美。同屬於大自然一份子的人類，也不停在各樣的建築或藝術品中追尋，渴望證明黃金比例與美的相關性。然而即使是世人眼中曠世巨作的大衛像，也沒辦法百分百貼近黃金比例，畢竟誤差永遠不能被全面消除，更別忘了有限的我們也無法窮盡無限的 φ 。正因爲黃金比例是一種人類無法徹底掌握的美，才迫使我們得以在追求美的道路上，不停努力地前進，再前進。

連自然都青睞的「黃金比例」近乎是「美」的同義詞。而我們的身邊，又有什麼東西用到黃金比例呢？

沒錯！就是這台 Creator Z16 筆記型電腦。

採用 16 : 10 螢幕的 Creator Z16 ，比市售的 16 : 9 螢幕多了 11% 的可視空間，創作更加自由寬廣。此外，16 : 10 ( 1.6 )也非常接近黃金比例（ 1.618 ），讓你在創作時，感受蘊含萬物奧秘、數學家兩千多年來淬鍊的「美」。

本著以人爲本的設計理念， Creator Z16 的觸控面板讓人可更直覺操作，隨時揮灑靈感。 90 Whr 的大容量電池搭配快充功能和 15.9 mm 纖薄金屬打造的 2.2 kg 機身，可完美配合現代人隨時行動隨地工作的步調。以 True Pixel 顯示技術打造的 QHD+ 超高畫質面板，加上獨家 True Color 技術於出廠前進行色彩校正，可以精準呈現璀璨畫面。

想堅持你對生活的美學，又不想放棄實用主義的追求？小孩子才做選擇，你可以通通都要！就讓融合黃金比例又兼具堅强實力的 Creator Z16，成為你的繆思女神吧！

現在購買 Creator Z16 加贈價值 2190 元 Microsoft 365 個人版一年期！登記再抽潮到出水的 Porter 托特包，這麼好康還不快點到賣場逛逛！

參考文獻