寶可夢我們談過,現在~我們要換個世界囉!(跳)
五彩繽紛的魔物獵人世界,裡面的魔物擁有各式各樣能力,小則噴噴口水、大則毀天滅地。隨著冰原的開放,迎來了最新一次改版(筆者是玩 pc 版)。就讓我們一起進入魔物獵人的空想科學世界,來一起研究研究這些魔物們的能力吧!

為什麼這篇文章空想魔物獵人會產生,有很大一部分歸功於《魔物獵人世界:Iceborne》中的封面魔物:冰呪龍。
可以自在的操控寒氣、釋放極低溫的吐息,還能從空無一物的空間產生冰塊,讓筆者在狩獵中不斷地思考:
這到底是怎麼辦到的?牠到底是怎麼在這麼短的時間內造出這些冰塊?這到底有多誇張?
自古以來運用冷凍能力一直是怪物世界常有的能力之一,那冰呪龍又有多厲害呢?
我盡量聚焦在 3 個冰呪龍的招式:
空中製造冰塊、製造冰牆和大絕招──同心圓冰牆。
像下面這張就是很棒的示意圖,畫面中我們可以同時看到了兩個很標誌性的招式:冰牆還有冰塊攻擊,還有我的獵人拿著冥赤龍銃槍站在那邊,一邊拿著冰塊敷臉一邊當比例尺。
以下這整篇文章都先假設獵人的身高為 180 公分來做計算,一起來討論這幾個招式多麼誇張吧。
整個國家都比不上的冷氣壓縮機
每當冰呪龍朝天空嘶吼,空氣中會產生數個漂浮的寒氣,然後凝結成冰塊落下,這些冰塊雖然呈現不規則的星形,但為了方便計算,我們就姑且假設它們都是半徑 1 公尺的球體吧!
然後帶入球體積方程式:4/3×π×半徑3,每個冰塊體積差不多是 4.2 立方公尺,而冰的密度跟液態水相比稍微低了一點點,大概0.9167 公克/立方公分,也就是是每立方公尺 917 公斤,這樣換算每一顆冰塊重量差不多是 4.2×917=3851 公斤⋯⋯原來我們的獵人都是被重達3公噸的冰塊打到啊!
至於另一個招式冰牆,是當冰呪龍朝地面噴氣時產生的。這些冰牆都成鋸齒狀、高度參差不齊,體積很難計算,所以為了方便計算,我們都把冰牆視為長寬高分別為 9×1×3.5 公尺的長方體,這樣的話體積大概是 31.5 立方公尺,一樣代入冰的密度換算成重量,每面冰牆差不多重達 31.5×917=28886 公斤。
由於水凝結成冰塊是一種放熱反應,所以每當冰呪龍使用以上的招式時,都會有熱量釋放到周遭環境中,但同時當地背景氣候也會影響到達成這件事的難易度。而魔物獵人的世界中也充滿各式各樣的環境,有森林、沙漠、洞窟還有冰山;又因為冰呪龍雖然劇情中是在雪原發現的,但後來基本上全世界各地都找得到,所以我們就先以室溫 20 度、濕度 60% 這種舒服、普通的氣候為基準,來討論冰呪龍從大氣中變出冰塊會放多少熱吧~

要從 20℃ 的空氣中的水氣凝結出冰塊,整個過程大概會像這樣:20℃ 水氣 → 20℃ 水 → 0℃ 的水 → 0℃ 的冰 → -10℃ 的冰。每一個過程中的熱量變化分別是540卡+20卡+80卡+5.5卡,我們得到當每 1 公克的 20℃ 水蒸氣要變成 -10℃ 的冰,大概會放出 645.5 卡的熱量,而每1卡的能量差不多是4.184焦耳,也就是說整個放熱過程能量變化為645.5×4.184≒2700 焦耳。
所以參考之前我們已經算出來的重量,光是產生一個重量為3851公斤的冰塊,就會放出超過3851×1000×2700≒100 億焦耳的能量,而只是產生一面冰牆會就會放出高達28886×1000×2700≒ 780 億焦耳的熱⋯⋯
這有多誇張呢?我們常看到的一台 500 公升大冰箱,一整年的用電大概是 300 度,每一度電相當於一件功率為1,000瓦的電器在使用1小時之後所消耗的能量,差不多是360萬焦耳,所以換算一下一台500公升冰箱一整年就是用了300×3600000 ≒10 億焦耳的能量。冰呪龍光是揮揮翅膀、幾秒鐘內在空中產生一顆冰塊,就差不多是 10 台冰箱發功一整年的份量,而隨便往地面上噴出一面冰牆,就是 78 台冰箱運作了一整年份的結果。
如果把出招時間也考慮進去,把能量換算成功率,會發現跟國家級的用電量沒差多少⋯⋯而且別忘了,冰呪龍可以源源不斷地使用這些招式,例如同一段時間產生出 6 個以上的冰塊,或是同時有超過 3 面冰牆存在在場地上。
更別忘了還有大絕招!!!!!!!!!!

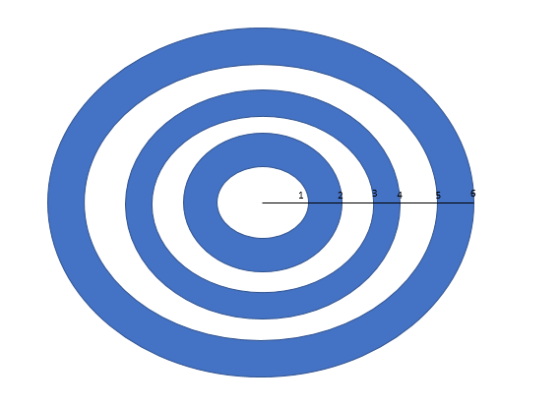
冰呪龍的華麗大絕招之一,就是起飛之後朝正下方噴出冷氣,產生數個成同心圓向外放射的環狀冰牆。
這個招式總共可以產生 3 個環狀冰牆,如下圖小畫家所示。我們先假設每一圈冰牆厚度皆為 1 公尺,藍色部分底面積就是不斷地做環狀底面積計算(大圓面積減小圓)然後相加,也就是(62π-52π)+(42π-32π)+(22π-12π)=66 平方公尺,再參考之前設定的牆高 3.5 公尺的話,這個招式產生的冰塊體積大概是66×3.5=231 立方公尺,換算重量大概是產生了211827公斤的冰,整個過程放熱高達不可思議的211827×1000×2700≒5720 億焦耳⋯⋯假設放招過程大概是 3 秒,功率已經不是冰箱可以比喻的了,這已經是全法國最高峰用電量的 4.5 倍。
真想知道冰呪龍平時到底是吃什麼才能累積這樣的能量⋯⋯
吸乾大氣造成生態浩劫的除濕機
現在我們知道了要產生這些冰牆和冰塊是多麼鬼扯的放熱現象了,但反正冰呪龍是古龍嘛~我們就假設他的能量是憑空變出來的,不再追究。但是有些東西可不能說有就有,就是這些水。
在冰呪龍本身好像沒有自備一大堆的水的情況下,答案好像滿簡單的,就是從大氣中凝結而來。
在氣溫 20 度、濕度 60% 的情況下,通常每 1 立方公尺空氣有大概 10.38 克水氣。今天要產生一面 31.5 立方公尺冰牆,我們需要 28886 公斤的水,如果要從空氣中抽取的話,這樣需要把將近 28886×1000÷10.38≒280 萬立方公尺空氣中的水都借來用。這大概是多少空氣呢?
拿足球場做個比喻好了~一個足球場面積是 7140 平方公尺,我們現在需要 280 萬立方公尺的空氣,所以光是產生一面冰牆,足球場上空大概 400 公尺內的水氣都會被吸光光。
假如冰呪龍要使用大絕招的話,會需要多達 21 萬公噸的水,所以總共需要的大氣量為211827×1000÷10.38≒2040 萬立方公尺,才能產生三個同心圓冰牆。如果一樣用面積為 7140 平方公尺的足球場來做底面,大概上空 2858 公尺以內所有水氣都會被抽乾…..提醒一下 阿里山森林遊樂區的海拔高度只有 2216 公尺而已喔~
而且我們以上的情況都是在 20℃、濕度 60% 的狀況下設想的,但是別忘了多采多姿的魔物獵人世界中,有雨林、沙漠、冰山、火山、洞窟,每個地方的氣候、濕度、溫度都不太一樣。但每個地方都計算的話篇幅又太長了,我們就簡單的設想一下,如果發生在其他環境會發生什麼事吧~

首先乾燥的荒原可能甚至沒有足夠的水分供給這些招式吧⋯⋯因為地球上沙漠地區的相對濕度基本上都低於 5%,溫度也很有機會更高,我看需要抽乾的大氣體積可能會幾十倍起跳,需要涵蓋的範圍會大到超過整張地圖。如果真的需要的話,可能連荒漠中的沼澤水都要借用一下,我看冰呪龍在這裡放出招式一定會造成泥魚滅絕~
其他地圖如古代樹森林、陸珊瑚台地,雖然是水分非常充足的地方,但是同時也住著許多需要這些水才能生活的動物,就算水分足夠給冰呪龍使用,一定會造成小生物的生態浩劫,例如水池乾掉、珊瑚萎縮,而我也從來沒看過有搖曳鰻魚乾躺在地上。
再來就是冰呪龍居住的雪原,既然都是主場,招式放不出來就太糗了。但有件事我們不能忘記,凝結是放熱反應,就算只有少量的冰塊產生,熱量也要有地方去吧?但我們也沒看過雪山融化之類的。
更重要的是⋯⋯我們操縱的獵人在這種周遭環境瞬間被乾燥、還附加超強大放熱反應的狀況下,不會覺得瞬間口乾燥嗎?這可是大概100台除濕機的強度啊!還有⋯⋯其實打冰呪龍要帶的是清涼、解渴的冷飲吧?
要操縱這股力量真是辛苦你了~