- 作者／西摩爾．派普特 (Seymour Papert)；譯者／張安昇、駱莊奇
柏拉圖在他的學院門口放了個標識，「只有幾何學家可入」。時代變了，多數試圖進入柏拉圖精神世界的人既不懂數學，對他的禁令也心安理得地視而不見。「人文文化」和「科學文化」之間精神分裂式的鴻溝使他們認為柏拉圖是個哲學家，哲學就屬於文科，就像數學就屬於理科。
「人文」和「科學」之間的巨大鴻溝貫穿於我們的語言、世界觀、社會組織構架、教育系統，在近年來甚至影響神經生理學理論。這一鴻溝還能自生自存：文化越分裂，分裂的各方越朝著相反的方向生長，進一步擴大分裂。
如我之前所說，電腦可以打破這兩種文化間的間隔。雖然文科學者覺得自己的工作是洞悉人性，冷冰冰的科學技術也幫不上忙。理科學者覺得文科太空泛，不具備科學研究要求的嚴謹性。但在我看來，電腦的出現可以從認知層面減少這兩種文化間的疏離。
當代文化對數學的集體恐懼其實來自於其疏離性。「人文主義」數學的誕生說明數學可以和人文研究相結合。在這本書中，我試圖解釋電腦如何讓數學知識更為人性化，讓兒童喜歡上數學。我想探討的不止是數學這門學科，更是重新看待學習過程的視角。
你是害怕數學，還是對學習感到恐懼？
許多成年人消極看待自己的能力短處，最常見的莫過於「放棄數學」了。數學沒學好的直接影響是就業受限，但其間接影響更為深遠。他們建立了一種世界觀，不同的知識被割裂開來，中間出現無法穿越的鐵幕。
我這裡主要想做的工作，不是要挑戰一塊塊知識領土的主權完整，而是清除人們跨學科思考的障礙。我不是要混淆數學和文學，他們雖然是不同的學科，但數學和文學在思維方式上的差異並沒有人們想的那麼大。所以在這本書裡我用了「數學國」這樣一個概念。在數學國，數學就是自然語言。
我用這個概念闡釋電腦的出現將如何把人文與數學／科學相結合。從數學國這個概念出發，我將論證電腦如何改變兒童數學教學方式，乃至於從根本上改變我們處理知識和學習的方式。
在我看來有兩種「數學恐懼症」。一種是對數學的恐懼已經達到心理學上「恐懼症」的程度，另一種與其說是害怕數學，不如說是害怕學習1。
在我們的文化中，患上厭學病的人不少於患厭數學病的人。兒童一開始讀書都很有幹勁，結果學習時受挫不斷，尤其是在學數學的時候。這磨滅了他們的熱情，使他們從一開始熱愛學習、喜歡數學，變得厭學且害怕數學。
我們要探索這一轉變是如何發生的，而電腦將如何避免兒童厭學，就要先回顧兒童學習的過程。兒童學得快是無庸置疑。以口語詞彙為例，兩歲時他們只會幾百個單詞，四年後一年級的孩子已經會說數千個單詞了。顯然，他們每天都在學習新詞彙。
孩子不是生來就有跟成人一樣思維
相對於詞彙量的積累，他們學數學的進度就沒那麼直觀了。皮亞傑畢生研究兒童智力的產生和發展，他的發現之一是成人往往不能理解兒童學習的內容和深入程度，因為從成人視角，從理所當然的知識結構出發，我們就看不見兒童究竟學到了什麼。皮亞傑的守恆（conservations）2理論就很好地解釋了這一點（見下圖）。
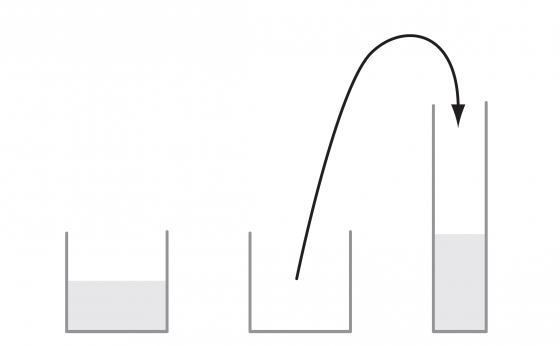
大人可以一眼看出把液體從一個容器倒進另一個容器裡，液體總量不變（灑出或殘餘在原杯中的少量水可忽略不計），這就是質量守恆。然而經皮亞傑的研究之後，人們才知道質量守恆這麼簡單的道理四歲的孩子可能完全不理解3。存量不因容器而改變，這個道理兒童要經過一定程度的智力發育才能理解。
此外還有數量守恆，大人知道計數時只要點清楚有多少件物品，用一個數字反映物品的件數，按什麼順序清點不會影響最終數額。但是兒童就不能把數額和物品脫離，他們的認識能力和世界觀無法理解為什麼不同的算數過程得到的結果都是相同的。
守恆的概念背後有一套看不見的龐大數學知識體系，需要兒童自己學習。要是叫四、五歲的孩子憑直覺回答，他們會說兩點之間距離最短的路線不一定是直線，兩點之間走得慢不見得就比走得快更花時間。他們這麼想不僅是因為缺乏「這項知識」，而是無法把最短線段、行走方式這兩個概念分離開來。
我們不能說孩子們無法理解這些概念是因為沒知識。皮亞傑發現兒童其實有一套自己的邏輯，雖然他們給的不是習以常見的答案，他們也能自圓其說。這些道理是兒童自發習得的，自成體系也非常完善。
習得的過程包括至少兩階段：早在學齡前時期兒童就有一套關於世界的理論；隨著他們成長，這套理論慢慢接近成人思維。這就是我所說的皮亞傑式學習法，它有效（所有孩子都學得了），成本低（不需要老師和教學大綱），人性化（不需要外部的獎懲措施，兒童自然而然就學會了）。
而許多人越長大越失去這種學習能力。有一部分人幾乎完全放棄學習，很少進行刻意學習。他們覺得自己沒有學習能力，也感受不到學習的快樂。這給個人和社會帶來巨大損失：在精神上和物質上，學習恐懼症都是個人發展的攔路虎。
其實你有能力，但卻被自己打敗！
大多數人沒有學習恐懼症，但他們或多或少會否定自己在某些方面的能力，說自己「就是學不好法語，聽都聽不懂」；「我肯定不會做生意，我對數字沒概念」；「我怎麼會雙板滑雪啊，我就是肢體不協調」。這些論調被他們奉為信條不斷重複，越發認定自己就是不行。
對於學習恐懼症的受害者來說，他們就認定自己學不了。這一章和第三章中的一系列實驗表明在友好的學習環境下，給予恰當的情緒支持和智力支持，四肢不協調的人也會雜耍，對數學沒概念的人不僅能學好，還會愛上數學。
自我強化的力量是很可怕的，要是一個人堅信自己不懂數學，一看到跟數學相關的事就躲，自暴自棄的下場就是進一步強化「不懂數學」的信念。最糟糕的是，這樣的信念不僅存在於個體中，更植根進我們的文化裡。
我們的文化把人分成了「聰明人」和「笨蛋」。每個人都會偏科，不同科目的學習能力強弱構成一個人的社會身分。有的人叫「數學天才」，有的人叫「數學白癡」。兒童最開始的學習經歷往往決定了他們的偏科傾向。哪科沒學好，一受挫就覺得自己成了笨蛋，或者某科白癡（最常見的就是數學白癡）。他們一認定了自己是笨蛋，再不斷強化這個信念，自己也很難跳出這個死循環。
每個人的學習能力不同，各有各的局限。我們很難破除這種說法，不僅因為這個說法已被廣泛接受，還因為它貌似科學，心理學家也設計了學習能力量表對此進行證明。但我們用以下這個思維實驗，質疑現有測試學習能力的手段，究竟測到什麼。
現有的數學能力測試真的能分辨出真正的數學恐懼症患者嗎？
我們換一個角度，要是每天逼孩子花一小時在方格紙上畫舞步，參加舞步繪圖測試，考試沒通過就不能跳舞。孩子們會不會被逼成「跳舞恐懼症」？我們可以說那些通過舞步繪圖測試的孩子就是「舞蹈學習能力強」？反之，孩子們不情不願地做算術題，沒日沒夜地練習然後通過測試，這就算「數學能力強」了嗎？不太對吧。
有人說這麼類比不恰當，應該用心理學方法收集「科學依據」。然而當代教育心理學研究的，都是身處現實世界「反數學國」的兒童，是怎麼學數學，或者更恰當的說怎麼放棄學數學。我們可以用另一個寓言來比喻這種研究方法。
想像一下，十九世紀的時候有個人覺得馬車太慢，想要改進交通工具。他深信要創造新的交通工具，首先要研究透澈現有交通工具。他仔細研究各類馬車的異同，研究不同輪子、軸承和套馬方式怎麼提高馬車的速度。我們知道後來真的誕生了新的交通工具——汽車和飛機。
汽車和飛機是怎麼來的？是通過研究馬車怎樣跑得快就發明出來的嗎？並不是。
我們今天的教學研究探討的是現有的教學方法。很多研究探討了學生在理科教育上頗為受挫的現實問題，人性化地提出「好的」教學法需要適應學生學不好理科這一現實。
雖然這聽起來頗為人道，但我認為正是這樣的想法讓教育機制停滯不前。這就像研究什麼樣的軸承可以提升馬車車速，而真正解決問題的是用汽車取代馬車。教育界需要發明出自己的「汽車」——突破性的教學法，而這也是本書的主題。
註解：
- Mathematic 的詞根 math、或 mathetic 出自希臘，有學習之意，例如 polymath 指博學之人。
- 譯注：心理和教育學界則常譯為「保留」。
- 自從有人類以來就有孩子，但我們居然要等待皮亞傑的出現，來解釋兒童如何思考，以及成人是如何忘記自己作為兒童時是如何思考。這不禁讓人聯想到佛洛伊德的認知壓抑理論。
——本書摘自《MINDSTORMS：Children,Computers,And Powerful Ideas 思維風暴：兒童如何用電腦建構無限可能》，2020 年 3 月，台科大圖書。
a0921003785彼得 潘
