- 本文接續上一篇:〈連發動戰爭也會選擇困難?幸好,數學家發明了「賽局理論」──《囚犯的兩難》上〉
許多科學中的重大進展是源於具有洞察能力的人,在看似不相關的事物中找到一些共同的要素。賽局理論也是如此。馮紐曼發覺在客廳玩的遊戲中蘊含著基本的衝突。隱藏在撲克牌、棋子、骰子背後的這些衝突深深吸引了馮紐曼,他在經濟學、政治學、日常生活以及戰爭中也觀察到類似的衝突。

在馮紐曼的術語中,「賽局」就是一種衝突的態勢,在這種態勢下,一個人必須做出某種選擇,並且知道對方也在做選擇,所有選擇將決定衝突的結果。有些賽局簡單而易於分析;有些賽局則因為參與者不斷做猜測而很難分析。
馮紐曼想知道賽局(尤其是有許多虛張聲勢和相互猜測的那類賽局)是否總是存在一種理性的玩法,而這正是賽局理論的基本問題之一。
你可能會天真地以為每一種賽局必然有一種理性的玩法。一定是這樣嗎?馮紐曼想弄清楚這一點。世界並不總是合乎邏輯,我們的日常生活中充斥著那麼多的非理性。更有甚者,像撲克牌遊戲一樣,相互猜測可能引發無窮盡的循環推理。理性的玩家對於如何進行遊戲,也不一定有明顯的結論。
缺乏天才的數學家或許也能發現上述問題,但只能無能為力嘆口氣,重新退回做「嚴肅的」研究。馮紐曼則不然,他抓住這個問題不放,以數學的嚴密性去對付它,終於獲得了非凡的證明。
正解在此!最理性的選擇,最佳的局面
馮紐曼從數學證明了在雙人賽局中,只要彼此的利益完全對立,就永遠存在一個理性的行動方針。這一證明被稱為「大中取小定理」。

這個定理所涵蓋的賽局種類包括簡單的井字〇╳遊戲到非常複雜的棋類遊戲,它適用於所有一輸一贏的兩人遊戲(這是符合賽局雙方利益「完全對立」要求的最簡單情況)。馮紐曼證明在這樣的賽局中,總有一種「正確的」玩法,或者更確切地說,「最佳的」玩法。
如果大中取小定理就是上面所說的這一些,那麼它最多就是對「娛樂數學」的一個挺不錯的貢獻罷了。實際上,馮紐曼看出了其中蘊含的更深意義。他意圖把大中取小定理作為基礎,延伸到包含所有其他類型賽局的賽局理論,例如兩人以上的賽局、參與者利益部分重疊的賽局等等。經過這樣擴充以後,賽局理論就可以適用於所有類型的人世衝突。
馮紐曼和摩根斯坦把賽局理論當作經濟學的數學基礎。在他們眼中,不同的經濟衝突可以看成各種「賽局」,以賽局理論的定理來分析。競標一項工程的兩個承包商,或者在拍賣會上競相出價的一群買主,都纏繞在互相猜測的微妙賽局之中,值得做嚴密的分析。

賽局理論幾乎從一開始就被視為一個重要的新領域而受到推崇。對馮紐曼和摩根斯坦的著作,《美國數學學會學報》有一篇書評預言:「我們的子孫會把這本書當作二十世紀前半葉最重要的科學成就之一,因為該書的作者們已經成功創建了一門真正的新科學──經濟科學。」在《賽局理論與經濟行為》出版以後,賽局理論及其術語成為經濟學家、社會科學家和軍事戰略家口中十分流行的行話。
賽局理論一生的對手?──「囚犯的兩難」
蘭德機構是最早接受並應用賽局理論的地方之一。蘭德是二次大戰結束後不久根據美國空軍的要求而建立的智庫,最初目的是完成洲際核武戰爭的戰略研究。蘭德聘用了許多戰時從事國防工作的科學家,逐漸發展為擁有眾多顯赫思想家的著名諮詢機構。
聘請馮紐曼為顧問的蘭德機構對賽局理論極為重視,投入極大的力量,不僅研究賽局理論的軍事應用,也對賽局理論本身進行基礎研究。在一九四〇年代末和一九五〇年代初,馮紐曼是位於加州聖塔莫尼卡的蘭德機構總部的常客。
一九五〇年,蘭德機構的兩位科學家佛拉德和德萊歇提出了賽局理論問世以來影響最大、看似簡單卻難解的一種賽局,也就是「囚犯的兩難」這幾乎動搖了賽局理論的部分基礎。
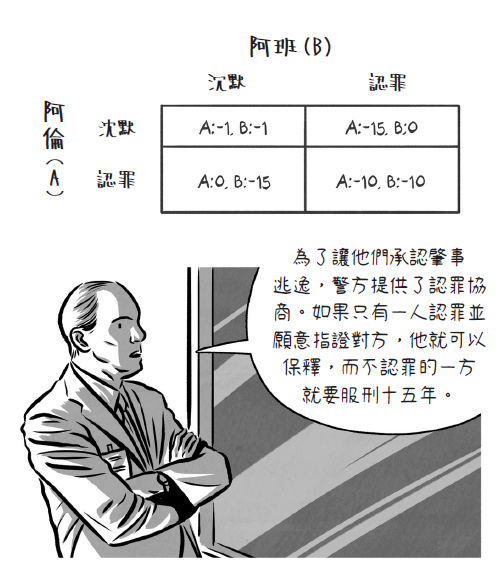
「囚犯的兩難」這個名稱是蘭德機構的顧問塔克所取的,因為塔克為了說明這種賽局而描述出一個有關囚犯的故事,對此書中第六章將會再詳細介紹,暫時我們只要知道它是極難思索的衝突處境,至今仍使我們困惑不已。

研究民間傳說的人知道,兩難困境的故事中會出現難以決斷的局面,讓聽故事的人苦思該怎麼辦。囚犯困境也是這一類故事,它的結局是留給聽故事的人或讀者一個解不開的難題。囚犯困境發明以後並沒有立即公開,在一九五〇年代只是在科學界口頭傳播,但它確實滿足民間傳說的研究者對兩難故事所下的定義。
當然,囚犯困境不只是一個故事,它既是一個精確的數學結構,也是現實生活中的一個問題。從一九五〇年囚犯困境「被發現」的時代背景來說,它其實沒有看起來的那樣神祕,因為當時大家正嚴重關切核武擴散和軍備競賽。事實上,早期核武時代的緊張形勢正是出現囚犯困境這種賽局的原因。
以犧牲共同利益為代價而使一方獲得安全的這般苦惱問題,並非核武時代的新問題。自有戰爭開始,這樣的問題就存在了。
但核武攻擊的突發和毀滅性使這個問題更加凸顯。我們可以毫不誇張地說,囚犯困境是國防的核心問題,而每個人對此的反應都不能被證明對錯,但可以從這些反應中看出誰是保守派、誰是自由派。
本書並不是談軍事策略的書。囚犯困境是一個普遍的概念,理論家們現在已經體認,它會發生在生物學、心理學、社會學、經濟學、法律等領域。只要有利益衝突的地方,就會有囚犯困境,而利益衝突並非只發生在有感知能力的生物之間。

對於動物和人類社會為什麼呈現目前的社會組織型態,囚犯困境的研究有很強的解釋能力。這是二十世紀所出現的最偉大思想之一,它簡單得任何人都可以掌握,又具有極大的重要性。
在馮紐曼生命的最後幾年裡,他看到現實戰爭變得愈來愈像虛構的兩難困境,或者說像他的理論中的抽象賽局。核武時代的危機常常被歸咎於「技術進步超越道德進步」。這一結論使人沮喪,使人懷疑道德進步是否還存在,以及原子彈越做越大,人類是否還能如以往存活。囚犯困境已成為當代最基本的哲學和科學課題,它和我們的生存緊密相關。
當代賽局理論的應用者試圖創造一種道德進展。有沒有什麼方法可以在囚犯困境的賽局中促成共同的利益呢?試圖回答這個問題,是我們這個時代最重大的知識挑戰之一。