美妙地證明 π 是超越(自然)數有什麼好處:無理數根本不存在,為什麼要研究這這一類的問題呢?
——Leopold Kronecke 德國數學家(1823-1891)

自 1988 年以後,每年 3 月 14 號那天,全世界就有許多數學家以各種方式慶祝數學常數圓周率 π(希臘字母,音「派」,其值為 3.1415⋅⋅⋅⋅⋅)。10 歲的外孫女陳佳璐似乎也受到波及,但她只知道「今天是派日」,卻不知道什麼是「派」。筆者自告奮勇地想幫她開通,謂「那不是可以吃的餡餅(西式餡餅 pie,音派),而是圓周與直徑的比例;4、5千年以前人類就已經發現圓周是直徑的3.1415⋅⋅⋅⋅⋅倍,….」。
既然不能吃,陳小姐是一點興趣都沒有,可是筆者卻突然想得:如果是倍數,怎麼小數點後的位數永不停止或重複呢?
圓周率怎麼就「無理」了?
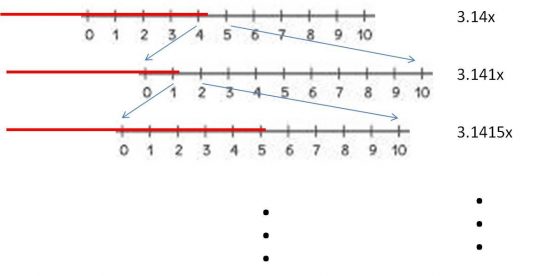
如果我們將直徑定為一公尺,並內分成 10 小格(即每小格為一公寸),則切斷之圓周的一端將落在第 3 公尺後之第 2 個小格內(在 3.1 公尺到 3.2 公尺之間);如果我們將 3.1 公尺– 3.2 公尺之空間放大,並內分成 10 小格(即每小格為一公分),則圓周的一端將落在 3.1 公尺後第 5 個小格內(在3.14公尺–3.15公尺之間);如果我們再將 3.14 公尺– 3.15 公尺之空間放大,並內分成 10 小格,則圓周的一端將落在 3.14 公尺後第 2 個小格內(在 3.141 公尺–3.142 公尺之間);……;如此繼續下去永遠沒有終止!圓周不是有固定的長度嗎?筆者很難想像這怎麼可能!
圓周與直徑都具固定的長度,當我們將直徑定為 1 單位時,圓周的長度將是 3.14⋅⋅⋅⋅⋅個單位;當我們將直徑定為 2 單位時,圓周的長度將是 6.28……個單位;……;理論上我們不是一定可以將直徑分成更小的 n 個單位、使得圓周的長度是整數 m 個單位嗎?
公元 1761 年,瑞士科學家兼哲學家 Johann Heinrich Lambert 證明了其答案為「不可能」:圓周與直徑無法找到一個公約單位[具「不可通約性」(incommensurability)]。
因為不可能「理解」,我們現在稱這種無法以兩個整數 m/n 來表達的「數」為「無理數」(irrational number)。
不能「理解」的無理數
事實上古希臘哲學家早就知道這種「無理數」的存在!
發現畢氏定理的畢達哥拉斯(Pythagoras,公元前 570年 – 495 年)是希臘哲學家,創建了一個後來被稱為畢達哥拉斯兄弟會(Brotherhood of Pythagoreans)的團體,致力於數學研究。他的政治和宗教教義在地方上眾所周知,深深地影響了柏拉圖、亞里士多德的哲學、以及他們以後的的西方哲學。
根據亞里士多德的說法,畢達哥拉斯人是為了神秘、而不是實際應用的原因而使用數學;他們相信世界上所有事情都是由整數組成的。因此當其哲學家西柏索士(Hippasus)透過畢氏定理發現兩邊由一個單位長度組成的正三角形,其斜邊 √2 為一無法以兩個整數 m/n 來表達時,他們認為西柏索士將此一神聖的上天秘密洩露給外人,因而將他拋棄到海上淹死懲罰。
同場加映:證明 √2 是無理數
令 √2 =m/n ==> m或 n 必定有一個是奇數(否則可以用 2 約分)
兩邊平方 2=m2/n2
2n2 = m2 ==> m, m2 必須是偶數
令 m =2x
2n2=4x2
n2=2x2 ==>n, n2必須是偶數
所以 n 及 m 均必須是偶數,違反了當初的假設;所以當初的假設一定是錯了,所以√2 不能以 m/n 表示,√2 為一無理數。
純邏輯推理推導出的矛盾
筆者在「數理化科學裡有天才嗎?」一直強調數學是一個純邏輯的科學,因此可能有年輕的天才;可是純邏輯推理怎麼會導出一個這些讓人無法理解的數字呢?讓我們在這裡再看一個例子。{3,8,6} 在數學上稱為有三個成員的「集合」(set),在這集合裡我們可以找出八個子集(sub-set):{}、{3}、{8}、{6}、{3,8}、{3,6}、{8,6}、{3,8,6}。
透過邏輯推斷,我們將可以得到結論謂:一個集合的子集數(8)將永遠大於其成員數(3)。
但如果我們將這一結論衍伸用到 {所有的集合},則其子集數將大於所有的集合數!可是「所有」的集合已經包含了「所有的集合」,怎麼還有比它更大的子集(集合)?
「不完備性定理」的提出,邏輯矛盾的不可避免
類似的觀念問題——「無限小」(infinitesimal)——也在微積分裡發生了,因此讓數學家感到頭大!1920 年,當時最偉大的數學家希爾伯特(David Hilbert1)終於忍受不了,提出「希爾伯特計劃」(Hilbert program),希望將數學建立在一個堅實而完整的邏輯基礎上。他要一勞永逸地從數學世界中消除這些問題,宣稱:
我們都相信每個數學問題都可以解決。畢竟,當我們將自己獻身於數學問題時,吸引我們最大的原因之一正是在我們的內心深處,我們總能聽到這樣的呼喚:這就是問題所在,你可以通過純粹的思考去尋求解決的方案⎯⎯因為在數學中沒有無知的東西。
1930 年,24 歲的年輕無名小子、維也納大學的博士生哥德爾(Kurt Gödel)在一國際會議上卻發表了一篇被認為是「現代邏輯中獨特和巨大的一座里程碑」。在「不完備性定理」(incompleteness theorem)裡,哥德爾證明了:在至少包括算術在內的任何非矛盾(consistency)之形式系統 (formal system) 裡,都不能通過自己的公理證明其完整性(completeness)。他說:
「人們可能會推測,這些公理和推理規則足以決定:可以在這些系統中正式表達的任何命題(待證之問題)。(我)將會證明……事實並非如此。」
哥德爾之「不完備性定理」粉碎了希爾伯特的宏偉計劃!

「我在說謊」這句話在文法上是完全正確的,其語意也非常清楚。但是我們卻沒辦法證明它(句子本身)是否正確:如果我是在說謊(假設),那這句話便是正確的,表示我不在說謊(結論),「結論」違反了「假設」,在邏輯上我們說「假設」一定是錯了(這正是我們證明√2是無理數的方法);好吧,那我們就改一改「假設」謂我不在說謊,那上句話便是不正確的,所以我是在說謊(結論),「結論」又違反了「假設」!
對於敬畏數學的人而言,數學是確定性的範式,是完美和絕對真理的典範;因此像「我在說謊」這種不符合邏輯的「命題」,在數學上是不應該、也不會發生的!沒想到哥德爾竟然證明了「事實並非如此」!原來數學也有其無法理解、不精確、和不確定性——對數學感到恐懼的學生,現在總算有理由了(不用謝謝筆者)!
結論:現實與抽象,那些難以解決的命題

在「經驗的困境2」二文裡,筆者提到我們如果「盲目」地將日常生活中的經驗擴展到物理學上,將碰到許多難以「理解」的困境:例如光既是「波動」又是「粒子」⎯⎯兩個水火不相容的觀念!
物理是實驗的科學,它的目的就是要解釋我們經驗到的現象;經驗強迫我們接受一些「不合理」的解釋3。數學沒有這一個要求,它可以通過純粹的思考去尋求解決的方案;可是從上面的分析看來,數學似乎也好不到哪裡:也有解決不了的命題?!這類發現顯然證明了「在現實之外,還存在有無法用物理驗證之更深層真理的知識」。
或許正如畢達哥拉斯兄弟會所相信的:人類之外還有一個神聖的上天!愛因斯坦有一句名言是:「我想知道上帝如何創造這世界。」只是,正如人工智慧的機器能有創造它們之人類的想像力嗎?我們如果是上帝創造的,我們能有上帝的想像力嗎?我們能跳出上帝的手掌嗎?
註解
- 某些科學家認為希爾伯特比愛因斯坦更早提出廣義相對論之場方程式!事實上兩人曾經為這一爭論搞得很不愉快。最後愛因斯坦寫信給希爾伯特尋求和解:「在我們之間(明顯地)有一種不愉快的情緒,但我不想分析其原因。我曾經抵抗它所導致的苦澀,並已取得了相當圓滿成功。我現在再次以無瑕的友誼想到你,也求你對我這樣做。 客觀地說,如果兩個在這個破舊世界中取得了重要成就的好夥伴,但卻彼此不能從中間獲得快樂,那將是很遺憾。」希爾伯特顯然接受了和解。對數學能力極強的希爾伯特來說,找到重力場方程事實上是一件小事,因此他不認為這是一個大成就;但愛因斯坦是奮鬥了 10 年才見到曙光。做為一個數學家,希爾伯特對場方程式的物理意義的了解,當然遠遠不及愛因斯坦;所以大部分的物理學家均認為愛因斯坦是第一位提出廣義相對論之場方程式的物理學家。
- 「我愛科學」,台北市華騰文化有限公司出版(2017年12月)。本書收集了筆者自 1970 年元月到2017年八月間在科學月刊及其他雜誌發表過的文章。
- 愛因斯坦不肯接受現在廣為物理學家所接受的量子力學物理觀(見註二之「愛因斯坦的最後一搏—EPR悖論」);例如他對光的看法是:「這將近五十年來對「光量子到底是什麼」的深思,並沒有使我更接近答案。現在每一個人,像張三、李四、王五等,都以為他們了解,可是他們錯了!」