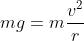今晚，我想來點……圓周率的派（π）！

本文由 新萃 Nutri Source 委託，泛科學企劃執行。

你有發現家裡的狗狗經常舔自己四肢，或是身上出現不明紅疹？當心這可能是過敏反應。寵物和人類一樣，也會有過敏反應，過敏可依照「來源」分為三種：吸入性過敏、接觸性過敏和食物性過敏。

不管是哪一種過敏反應，在人的身上都比較容易發現和排除。但狗狗的過敏卻很難處理，如果是接觸性或吸入性過敏，即使你把家裡打掃得很乾淨，還是無法排除帶狗出去散步時可能接觸到的環境過敏原。因此，對飼主來說，最容易控制的是食物性過敏。

食物性過敏是怎麼發生的呢？其實，「食物過敏」這個詞並不太準確。正確的臨床醫學用詞是「食物不良反應」（Adverse Food Reaction, 簡稱AFR）（Jackson, H. , 2009），指的是吃下食物後身體產生各種不良反應。並進一步分為食物過敏（Food Allergy）和食物不耐受（Food Intolerances）兩種。

如果你看過動漫作品《工作細胞》，你就會知道過敏其實只是免疫系統對特定成分產生的過度反應，因此全名為「過分敏感」；而食物不耐受則並非免疫性反應，而是消化系統無法代謝或對該生物體有毒，例如狗不能吃洋蔥或巧克力，否則會致死等等。

由於寵物沒有選擇權，只能吃飼主提供的食物，如果飼料中恰好有會造成牠 AFR 的成分，就可能產生各種症狀。除了腸胃發炎和拉肚子外，最明顯的外在症狀就是皮膚問題，包括搔癢、脫毛和紅疹等。後者容易被誤判為皮膚性疾病，讓許多飼主狂跑獸醫院的同時，獸醫也難以對症下藥。

雖然曾有研究透過讓醫師用血液或唾液是否檢測出 IgE 抗體來判斷狗是否過敏（Ermel, R et al.,1997），但最新的研究卻發現，無論使用無論血清的 IgE 抗原或是唾液裡的 IgM 或 IgA 抗原都無法有效檢測出狗狗的過敏來源（Udraite Vovk Let al., 2019 & Lam ATH et al., 2019），甚至會造成偽陽性誤判。因此，目前學界公認唯一能識別食物過敏原的方法就是「食物排除法」（Food Elimination Method）。

食物排除法的原理相當簡單粗暴，類似我們過去在學校做的實驗一樣，抓出「控制組與對照組」。首先，將狗狗的食物換成牠沒吃過、單一來源且易消化的高蛋白質或水解蛋白質；同時嚴格限制牠對其他食物接觸，包括其他人餵食或路上亂吃等可能性都要注意，此為「對照組」，如此持續 8～12 週，觀察皮膚是否有改善。如果確實有改善，那就證明了確實是 AFR 而非皮膚病。

下一步我們可以進行「食物挑戰」，在每餐食物中逐一嘗試可能的過敏原（例如常見的牛肉、雞蛋等），有如「控制組」，等到症狀又出現，就可以確認哪種食物成分是過敏原，未來就可以在飼料中排除，讓狗狗健康快樂地成長。

這個方法需要飼主的大力配合和耐心紀錄，不僅要在漫長的試驗期，更需要在控制期一一排除所有不可能之後，才能找到答案。而其中最困難的部分，也是實驗的基礎可能是第一步：「提供狗狗牠從未吃過，且肉品單一的蛋白質」，這點對多數飼主來說幾乎是不可能的任務，因為大部分的寵物飼料成分都很複雜。不要說狗狗了，搞不好你連自己沒吃過什麼恐怕都不知道。

那該怎麼進行食物排除法呢？別擔心，沒有找不到的肉品，只有勇敢的狗狗。市面上已經有了針對過敏狗狗的低敏飼料，新萃推出了一系列低敏肉，包含單一肉種的袋鼠肉、鹿肉以及野豬等相比牛豬羊等較不容易取得的肉類，是進行食物排除法第一步測試的首選。

此外，新萃牌無論哪種飼料都有美國專利 Good 4 Life® 奧特奇專利保健元素，能促進飼料中的營養都被狗狗完整吸收。不僅過敏的狗狗能吃，有消化不良症的狗狗也適用。

• 新萃產品說明

參考資料

1. Thus for the purpose of this discussion, although the term food allergy is used throughout, it should be recognized that this term is a presumptive clinical diagnosis and adverse food reaction is a more accurate term for these canine cases. – Consensus
2. Jackson, H. (2009). Food allergy in dogs – clinical signs and diagnosis.. Companion Animal Practice.
3. Assessment of the clinical accuracy of serum and saliva assays for identification of adverse food reaction in dogs without clinical signs of disease – PubMed (nih.gov)
4. Lam ATH, Johnson LN, Heinze CR. Assessment of the clinical accuracy of serum and saliva assays for identification of adverse food reaction in dogs without clinical signs of disease. J Am Vet Med Assoc. 2019 Oct 1;255(7):812-816. doi: 10.2460/javma.255.7.812. PMID: 31517577.
5. Direct mucosal challenge with food extracts confirmed the clinical and immunologic evidence of food allergy in these immunized dogs and suggests the usefulness of the atopic dog as a model for food allergy. – Consensus
6. Ermel, R., Kock, M., Griffey, S., Reinhart, G., & Frick, O. (1997). The atopic dog: a model for food allergy.. Laboratory animal science.
7. https://www.moreson.com.tw/moreson/blog-detail/furkid-knowledge/pet-knowledge/dog-food-allergen-TOP10/
8. 狗狗因為食物過敏而搔癢不舒服，為什麼做「過敏原檢測」沒什麼用？
9. 【獸醫診間小教室】狗狗皮膚搔癢難改善？小心食物過敏！ – 汪喵星球 (dogcatstar.com)
10. 寵物知識+／毛孩對什麼食物過敏？獸醫：驗血完全不準！診斷法只有一個 | 動物星球 | 生活 | 聯合新聞網 (udn.com)
11. Is there a gold-standard test for adverse food reactions? – Veterinary Practice News

• 作者／賴昭正｜前清大化學系教授、系主任、所長；合創科學月刊

今年 7 月的科技頭條，應是 11 日及 20 日兩架載著只須穿連身衣（不是專業宇航員在發射或著陸時穿的加壓宇航服和頭盔）之「一般老百姓」的太空艙，飛到太空邊緣後又成功返回地球，這一壯舉標誌著人類商業「太空旅行」（space travel）新時代的開始。

這兩架太空艙的軌跡基本上是相同的，我們以後者（7 月 20 日）的發射為例，為大家大略說明「太空旅行」到底是怎麼一回事。

太空火箭從地面垂直向上發射，進行大約 110 秒的動力飛行到三倍音速、高度為 76 公里處時，火箭減速，乘員艙與之分離，靠其慣性動量、在無動力推動下繼續向上衝刺飛行；因地球引力（重力）不斷地往下拉，衝到約 100 公里的高度，即開始反方向加速折回地面。進入大氣層時，因為空氣阻力而開始減慢，最後在降落傘的幫助下慢速著陸。總共飛行時間大約為 10 分鐘。

本文主要是討論太空旅行及無重量感（weightless）的物理，只在結論時才略微提及太空旅行所造成的社會觀感。

沒辦法讓飛機飛的地方都是太空——卡門線（Kármán line）

相信許多讀者都跟筆者一樣，認為太空是一個遙遠的地方：那裡不但沒有地球引力，也沒有空氣。筆者實在沒想到所謂的「太空旅行」，若不是因為 90 度的斜坡車子開不上去，100 公里的距離，其實只要開車約一個小時即可到達！

高空 100 公里處的氣壓只有地球表面的千萬分之一，也比一般客機飛行之 8-12 公里高度高得多，但那裡的地球引力卻還是非常強：只比地球表面的引力小了 3% 左右而已。

為什麼「太空」定在那裡呢？我們知道飛機是靠機翼上下空氣壓力不同上升的^[註1]，因此飛機在沒有空氣的空間是沒辦法飛行的。

航天先驅卡門 (Theodore von Kármán^[註2]) 在一國際會議中提出因為空氣太稀薄了，在海拔 100 公里處上方行駛的物體，需要一個不依賴地球大氣層產生升力的推進系統^[註3]，因此在 1960 年代，國際航空聯合會（Federation Aeronautique Internationale）將海拔 100 公里處定為太空的界限——稱為卡門線（Kármán line），粗略地標出傳統飛機無法有效飛行的高度。

7 月 11 日的「太空旅行」只到 80 公里處就轉回，因此依這一定義，不能算是「太空」旅行。但在 1960 年代初期，世界上第一位太空律師海雷（Andrew Haley）依卡門的定義，更精確地算出空間的實際邊界應該在距離地面約 84 公里處。這個高度在「中層大氣」（mesosphere）處：中層大氣是地球大氣層的最外層物理邊界，流星通常在此處燃燒，在這裡要產生升力所需的飛行速度將超過「軌道速度」（見後「為什麼在靠近地球的太空站上，也能體驗無重量感？」段落）。

這個高度也是美國空軍在 1950 年代使用的高度：飛行高度超過 80 公里的飛行員可以獲得「宇航員機翼」（astronaut wings）別針。因為在太空界限下，空間是屬於個別國家，在它的上面則屬於「公空」；做為太空科技發達的強國，美國當然欣然採用這個定義。

不見浩瀚星河，只有四分鐘的無重量感體驗

如果地球只有籃球大小，則 100 公里的高空只是在籃球表面上的 1.1 公分處而已。在這樣的「高」度是不可能俯視到漂浮在太空中的地球的，只能像汪洋大海中的小船或天空中的飛機，看到天水（陸）交接的圓弧地平線而已。

因此太空旅行不可能是為了看「風景」，應該是為了體驗「沒有重量」。可是前面不是提過那裡的地球引力還是非常強的，怎麼會沒有重量？

地球的引力（稱為「重力」）本該讓我們往地球中心落下的，但是被地板或磅秤阻擋；地板或磅秤產生了反作用力（牛頓第三運動定律），所以人體就被夾在這重力與反作用力之間，產生了「重量」的感覺。

如果將地板或磅秤拿掉，則人體將因重力的關係繼續往下掉（稱為「自由落體」），因為沒有任何阻擋下掉的反作用力，我們不會有被壓迫的感覺，造成了「無重量」感：所以「無重量」只是一種感覺，並不代表我們沒有受到重力或任何力。

地球重力所產生的加速為 9.8 m/s² ，通常簡寫為 g。在 110 秒的火箭動力往上推動時，太空人會感受到比 g 更大的加速；但太空艙一脫離火箭後，他們會立即處於自由落體狀態（即使太空艙還在往上升），突然感到失重。這時 他們可以解開座椅釦子，在機艙裡面到處「漂浮」，在一個窗口輕輕一碰就可飄到另一個窗口、喝水、擲球……等，親自體驗無重量感的一些奇奇怪怪現象。

為什麼是「漂浮」呢？想像你是在一個自由落體的電梯中，如果從口袋中拿出一個蘋果，在面前張手將它放開，蘋果會下掉嗎？當然會，因為這不正是牛頓發現萬有引力的靈感嗎？

問題是你與電梯也是以同樣的加速在下降，因此對你與電梯而言，蘋果將「漂浮」在你面前不動的（牛頓第一運動定律）！如果太空艙內沒有空氣，你輕輕地推蘋果一下，蘋果將會加速（牛頓第二運動定律），當推動力消失後即沿直線「漂浮」地做等速運動（牛頓第一運動定律）！

事實上正是這一「領悟」，使愛因斯坦將只適用於等速參考坐標的狹義相對論，成功地擴展到適用於任何參考坐標之廣義相對論（參見「愛因斯坦一生中最幸運的靈感–廣義相對論的助產士」，2021 年 3 月號科學月刊）。

在大約四分鐘的失重體驗後，太空艙的下降將慢慢感受到空氣的阻力，使太空人慢慢感受到最高可達六倍重力的「重量」減速，最後靠降落傘緩緩著陸。

為什麼在靠近地球的太空站上，也能體驗無重量感？

地球之萬有引力是無遠弗屆，原則上我們是逃不出其如來佛的手掌心^[註4] ，所以要使太空艙不被拉回地面，主要有兩個方法：

1. 跟地心引力硬碰硬，例如往上衝的火箭。
2. 把地心引力當作物體圓周運動的向心力，若地心引力全用在圓周運動轉彎時的向心力上，地球引力就沒辦法吸落物體。

不免俗地，必須先看一下向心力的公式，當一質量為 m 之物體做圓周運動時，會需要向心力改變運動方向。牛頓物理告訴我們，這向心力（F）的大小與圓周運動半徑（r）成反比，並與運動速度的平方成正比：

當向心力與地球引力相等時：

兩邊的 ｍ 可以對消，因此不用考慮物體質量，只要考慮該物體位於多高的位置（圓周運動半徑），就能算出物體需要以多少速度前進，才不會被地球引力吸落，而這個前進速度，我們稱為「軌道速度」。

這正是國際太空站保持在高空約 400 公里處的設計原理：它以每小時約 28,000 公里平行於地球表面的速度前進，相當於每 90 分鐘繞地球一圈，一天的空間行程大約是從地球到月球再返回的距離; 而地球在赤道的自轉速率，大約為每小時 1,700 公里。

能設計將太空站或衛星固定在空間的某一點嗎？能，但超出本文討論的範圍，只好留給讀者自己去想了。

而在太空站內，由於地心引力全被當作圓周運動的向心力，所以「無重量」不只是「感覺」，而是在太空站內的物體真的沒有重量，沒有任何淨力作用於物體上！

想體驗無重量不用跑到太空——拋物線飛行

相信任何人初次經驗到無重量感都會驚奇得張口合不起來的：杯子的水倒不出來、一根手指就可以舉起在地面上重一公噸的物體、輕輕一跳就可以創世界紀錄。

可是需要花這麼大的人力、物力去製造這環境嗎？筆者年輕時就曾在遊樂場裡享受到大約一秒鐘、記憶猶新的無重量感；而如果你不怕摔得粉身碎骨的話，從台北 101 大樓往下跳，也可享受到大約 9 秒鐘的自由落體（生命可貴，千萬不要輕易嘗試） 。

1950 年，美國德州布魯克斯空軍基地（Brooks Air Force Base）空軍航空醫學院（Air Force School of Aviation Medicine）的哈伯（Fritz & Heinz Haber）博士兄弟就提出利用「拋物線飛行」（parabolic flight）來模擬「無重力」的建議。

現在「拋物線飛行」不但已經是美國國家航空和航天局（NASA）之宇航員訓練、科學實驗、及空間設備技術測試的平台，而且已經商業化了^[註5] 。「拋物線飛行」需要經過特殊訓練的飛行員來精確地操縱及控制飛機的飛行，在此我們僅簡單的介紹其原理如下。

從穩定的高空 8 公里處平飛姿態，改成 45° 上沖姿態飛行；在這個階段，體重是正常體重的 1.8 倍。這飛行持續約 20 秒後，機組人員開始執行一種稱為「注入」（injection）的機動降低推力，並操縱飛機軌跡使其遵循一種拋物線（投擲石頭在重力作用下的自由落體）飛行。垂直載荷係數在這個階段從 1.8g 降到持續約 25 秒的零重力（0g）感。最後在拋物線的下降部分執行與進入對稱的 1.8g 退出階段，在大約 20 秒內將飛機返回到穩定的高度水平。如此重複20-30次。

為了體驗無重量，值得飛出卡門線嗎？

美金萬元不到就可以「拋物線飛行」，體會無重力經驗，但卻已有 600 人預訂 25 萬美金去做 80 公里太空旅遊^[註6]。你說這不是財富和特權的粗俗展示是什麼？當然，那是他們「辛苦賺來」的錢，他們要怎麼用我們無話可說；只是在高喊減碳^[註7]及貧富不均的全球危機中，億萬富翁們卻在花大錢將自己送入太空尋找樂趣，似乎有點……

有「不以為然」想法的人似乎不只是筆者；事實上或許由於「心中有愧」，全世界最有錢的、此次太空旅遊公司之一的大老闆、亞馬遜公司創辦人貝索斯（Jeff Besos）在出發前宣布將捐贈 2 億美元給史密森學會（Smithsonian Institution）——這是自 1846 年史密森 (James Smithson) 創辦該巨大之博物館、教育、和研究綜合體以來的最大單筆捐贈；而這次太空旅遊拍賣一座位所得的 2000 萬美金也全部捐給慈善機構。

據 Treehugger 網路上的一篇文章「太空旅遊的碳足跡有多少？」（ What Is the Carbon Footprint of Space Tourism? ）分析，雖然這些太空旅遊每次會製造 60 到 80 公噸的碳足跡^[註8]，就其本身來看，這事實上並不算多：因為一架從芝加哥飛往香港的 777-200 飛機就輸出 351 公噸的碳足跡，每天還飛行多次！

但不要忘了後者承載約 300 人飛行 1.3 萬公里。該文最後結論說：但與這些富豪之私人飛機整年在多個住宅間飛來飛去，可能都微不足道；所以我們不是需要更少的火箭和更少的太空旅遊，而是需要更少的億萬富翁。不知讀者同意與否？

註解

• 註 1：空氣流動越快的地方，壓力越小［伯努利定律（Bernoulli’s Law），為一應用於流體的能量不滅定律］。機翼的設計就是使其上下的空氣流速不同。
• 註 2：匈牙利出生 ，在第一次世界大戰前後的幾年裡，參與直升機的早期設計等工作；1930 年，卡門移居美國，成為二戰期間火箭和超音速飛行的專家。1944 年，卡門和他的同事在加州建立了噴氣推進實驗室（Jet Propulsion Laboratory），為現在是美國宇航局的傑出實驗室。
• 註 3：火箭推進器靠的是動量不滅定律，所以可以在沒有空氣的地方飛翔。
• 註 4：實際上當然不是這樣。在「 霍金和黑洞：霍金一生的追尋讓我們知道了哪些事？」一文裡，筆者用簡單的能量不滅定律，導出要脫離地心引力的最小速度；在沒有空氣的阻力下，其值為每小時 40,284 公里。當然，在實際操作上我們並不一定要一下子提供這麼大的速度；我們可以分段加速，慢慢將太空推出地心引力之外。不知道讀者是否在這裡看出一個邏輯上難以理解的地方（參見「從圓周率與無理數，談數學也有其無法理解、不精確、和不確定性）」：地心引力與距離的平方成反比，所以地心引力可以趨近於零，但不會等於零（即永遠逃脫不了地心引力）。
• 註 5： 有興趣的讀者可以上網到「零重力公司」（Zero-Gravity Corporation）登記（美金 7500 元加稅）。
• 註 6： 現在已是 45 萬元美金起跳。
• 註 7： 聯合國氣候變遷小組（IPCC）7 月 9 日由 234 位科學家撰寫的 3000 多頁報告指出，地球暖化速度比科學家先前觀察到的還要快，全球均溫很可能在大約十年內就升高攝氏 1.5 度，突破巴黎協定的升溫幅度限制。
• 註 8： 貝索斯的火箭燃料是使用液態氫和液態氧，不會直接產生二氧化碳；因此氫正越來越多地被推廣作為應對氣候變化的一種方式。但絕大多數氫氣（96%）來自化石燃料，特別是來自甲烷及煤的氣化，其提煉時所產生的熱及溫室氣體其實不亞於其它燃料 [這情況很像不考慮發電可能造成更大的污染，而盲目地發展電動汽車一樣，詳見「我愛科學」（華騰文化有限公司，2017年12月出版）]。

每到了夏季，海邊總是大家嚮往的好去處（雖然現在因為疫情影響，我們提倡乖乖待在家裡為臺灣防疫盡心盡力！），過往夏季時大家前往喜愛的陽光沙灘，總可以看到陣陣海浪拍打在岸邊，盡情享受清涼海水與徐徐海風的吹拂！

但！海洋並非總是風平浪靜，有時的海洋也會帶給我們突如其來的巨變，在新聞中時常聽聞的瘋狗浪即為其一。

到底什麼是瘋狗浪？又為什麼要稱呼他為瘋狗浪呢？

在海面傳遞的能量——海浪

要了解瘋狗浪的成因，首先要先了解海浪是如何形成的！

海浪的主要成因是風將能量從大氣傳至海面，當海面獲得能量時，海洋中的水分子便開始做圓周運動，這，就是海浪！上層海水拖著下層海水，能量一層一層地向下傳遞，傳遞過程同時受到水分子之間的摩擦力影響，能量逐漸減弱，因此在深層的海洋幾乎沒有波動產生。

當海浪開始向前傳遞時，越接近岸邊，海床逐漸升高，下層的水分子撞到海面下的海床，就會造成海浪的波速逐漸減緩，我們以下面這張岬灣圖簡單判斷波浪傳到岸邊時與海岸呈現的交角關係。

當波浪（藍色箭頭）逐漸打進海岸時，受到海底地形的影響，其波速逐漸減緩，波浪逐漸偏向法線（黃色實線），越靠近海岸，波浪持續偏向法線，最終波浪前進的方向會與海岸漸趨垂直。

海岬上的突發大浪

海岬地形即是容易出現瘋狗浪的其中一個原因，從圖中可以發現，當海岬處波浪不斷聚集，能量匯聚會造成海浪的波高逐漸累積，此時的海岬，容易產生突發性的大浪，也就是我們俗稱的瘋狗浪。

另外，容易造成瘋狗浪的原因還有強風吹拂，當風速越強烈快時，海面獲得的能量就會更多，產生的海浪也會更為強烈，當強烈的海浪再加上碰到匯聚能量的海岬地形時，便更容易造成瘋狗浪的產生。

瘋狗浪並沒有明確的定義或是說法，因為瘋狗浪容易致在岸邊活動的人們於危險當中，就如同瘋狗一樣可能會亂咬人，所以我們習慣將突然發生或是強烈的海浪稱做瘋狗浪。

臺灣易發生瘋狗浪的時間與地點

在臺灣，最易發生瘋狗浪的時間便是颱風與東北季風盛行之季節：颱風強力的風速會在臺灣外海持續產生強烈的海浪，當海面不斷獲得能量，其傳至海岸邊的能量也會更多、更大；而冬季時的東北季風也是容易產生瘋狗浪的原因之一。

而臺灣的東北角因多為岬灣地形，則是瘋狗浪易出現的地點，但瘋狗浪並不局限於出現在東北角，只要有海岬地形，或是較為突出的堤坊、海岸都有可能匯聚能量，形成波高較高的海浪。所以當知道海洋上有氣旋產生、強烈的季風作用或是在岸邊感受到較為強力的海風吹拂時，都應盡量遠離岸邊才最為安全！

預知瘋狗浪—海洋雷達觀測系統

過去我們總認為海象難以預測（此海象非海洋中生活或是在海生館可以看到的海象，而是指海面上因為風力吹拂而造成海浪的情況！），因為海象預測需要考慮到風向風速的變化、海浪相互作用影響、海底地形等眾多原因，但風場環境瞬息萬變，間接也造成不斷變動的海象，再者，一般民眾較少需求接觸相關的海象預報，所以海象觀測一直不如氣象觀測發達。

台灣目前使用的為海洋雷達陣列推算海域中波浪的強度，發展出台灣海洋雷達觀測系統（Taiwan Ocean Radar Observing System, TOROS），提供給人民更為準確、進步的海象監測，即時性與預測性的海象觀測，使海洋運輸、漁業捕撈等工作或是休閒娛樂更加安全。

海洋雷達陣列是使用雷達發射雷達波，當雷達波入射到海表面時，碰到海洋中的海浪，便會以各方向散射，海洋雷達就是利用雷達波所產生的「布拉格效應」—當海洋上出現與雷達波波長有偶數倍數關係的海浪，會產生較為強烈且能量較大的雷達回波反射回雷達，來推算目前海面上波浪的波長！

而不同地點、距離會使回傳的回波產生相異的都卜勒效應，透過都卜勒效應（頻率為正值，代表海浪靠近雷達；頻率為負值，代表海浪遠離雷達）便可以知曉波浪與雷達的相對速度與方向。

當雷達透過布拉格效應獲得海浪之波長（因雷達波的波長為已知數），又知曉海浪頻率的變化後，將回波所得出之資料輸入電腦計算，便可以得出波浪的波高、波向、週期、速度等相關資料。

而難以預測的海象遇到瘋狗浪更增添了難度，因為瘋狗浪的成因與易發生地點都僅是推測性的預測而非絕對性的預測，專家目前對瘋狗浪的成因仍持續的嘗試理解與推估，但目前中央大學水海所團隊已經透過海洋雷達觀測系統，可以有效的在瘋狗浪抵達的前 20 至 30 分鐘提供預警！

透過分析瞬時的海象變化，更可以有效進行預測，也可較為減少瞬間海象造成的災難，海洋中的觀測系統仍在不停的發展與改進中，在未來，一定會持續的改良與精進海象觀測，加強海上或海邊活動的安全性！

資料來源：

1. 國立中央大學地球科學系
2. 神出鬼沒的瘋狗浪
3. 海洋觀測儀器與方法
4. 利用高頻雷達監測台灣四周海域表層海流