- 【科科愛看書】無論何時,只要想到數學就一個頭兩個大?那你肯定還沒看過《數學大觀念:從數字到微積分,全面理解數學的 12 大觀念》!此書從簡單加減到高深微積分,用嶄新的視角連結密碼般的數字和真實人生,循序漸進去探索數學的規律和其中令人讚嘆的美好。讓我們一起將數學砍掉重練,邁向數學偉大的航道吧!
π 數知多少? 真有如滔滔江水,連綿不絕啊~
只要仔細測量,你便可以用實驗的方法確定 π 稍微大於 3。但是自然而然浮現了兩個問題:
- 你可否在不用任何實質測量的條件下,證明 π 是一個接近 3 的數?
- π 又是否能用一個簡單的分數或是公式來表示?
第一個問題可以經由畫一個半徑為 1 的圓來回答,這個圓的面積是 π12=π。在下圖中,我們畫出一個邊長為 2 的正方形,將這個圓完整的包在裡面。由於這個圓的面積一定小於正方形的面積,這就證明了 π<4。
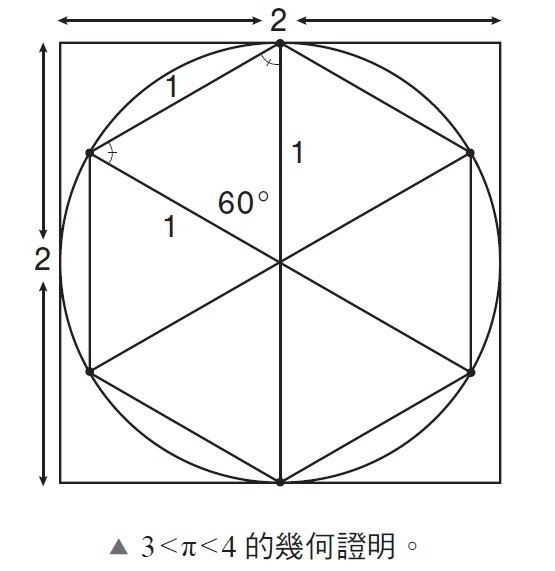
另一方面,這個圓包含了一個六邊形,它的六個角平均分布在圓周上。這個內接六邊形的周長是多少呢?六邊形可以分解成 6 個三角形,每個三角形都有一個 360º/6=60º 的圓心角,而且每個三角形中有兩邊是圓的半徑(長度為 1),所以它們都是等腰三角形。根據等腰三角形定理,另外兩個角有相同的角度,所以一定都是 60º。
因此,這些三角形都是邊長為 1 的等邊三角形。於是這個六邊形的周長是 6,而它一定比圓周 2π 少一點。因此 6<2π,也就是 π>3。將這些結果放在一起,我們就會得到 3<π<4。
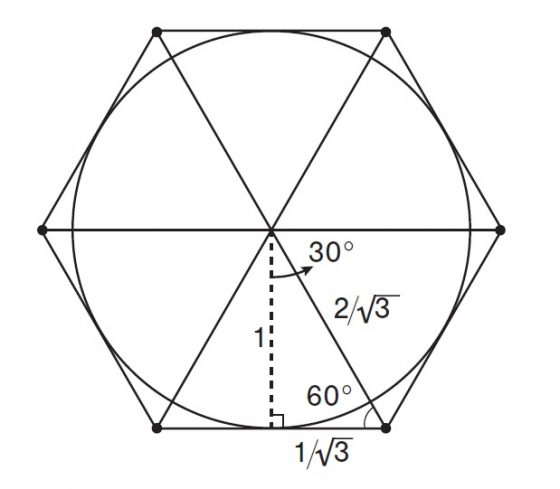
我們可以用具有更多個邊的多邊形來將 π 限縮在更小的區間中。舉例來說,如果我們不用正方形,而是用一個六邊形將單位圓包起來,就能證明 π<2√3=3.46……。
這個六邊形同樣可以被細分成六個等邊三角形,每一個三角形都可以再細分成兩個全等的直角三角形。如果較短的直角邊其長度為 x,那麼斜邊的長度就是 2x。根據畢氏定理,x2+1=(2x)2,我們即可解出 x=1/√3。
由此可知,這個六邊形的周長是 12/√3=4√3。而因為這個數大於這個圓的周長 2π,於是 π<2√3。(有趣的是,如果將這個圓與這個六邊形兩者的面積互相比較,我們也會得到相同的結論。)
根據這個結果,偉大的古希臘數學家阿基米德(西元前 287~212 年)進一步創造出 12、24、48 和 96 邊的內接和外切多邊形,並導出 3.14103<π<3.14271,以及一個更簡單的不等式:3 又 10/71<π<3 又 1/7
分數啊,請為我找到 π 吧!
用分數逼近 π 有很多簡單的方式,比方說:314/100=3.14、22/7=3.142857、355/113=3.14159292……。
我特別喜歡最後一個逼近式,因為它不只正確產生小數點後的前六位數,也把最初三個奇數各用上兩次:依序是兩個 1、兩個 3 和兩個 5!
當然,若能找出一個剛好等於 π 的分數會很有趣。(其中分子和分母都是整數,否則我們可以直接用 π=x/1。)不過,朗伯(Johann Heinrich Lambert)在 1768 年證明了 π 是一個無理數,也就證明了上述的嘗試徒勞無功。
或許 π 可以用某個簡單數目的平方根或立方根來表示?舉例來說,√10=3.162…已經相當接近了。
但是在 1882年,林德曼(Ferdinand von Lindemann)證明了 π 不只是無理數,還是一個超越數。也就是說,π 不是任何一個整係數多項式的根。舉例來說,√2 是一個無理數,但它並不是一個超越數,因為 √2 是多項式 x2−2 的根。
雖然 π 並不能用一個分數來表示,卻能表示成無窮多個分數的總和或乘積!舉例來說,我們在第十二章會看到:π=4(1-1/3+1/5-1/7+1/9-1/11…)
這個公式不僅美麗,也相當驚人,但在計算 π 的眾多公式中,它並不算是非常實用的一個。算了 300 項之後,我們仍舊不會得到比 22/7 更逼近 π 的數值。下面是另一個驚人的公式,我們稱之為沃利斯公式,它以一個無窮乘積來計算 π,不過同樣需要花很長的時間來收斂。
π=4(2/3×4/3×4/5×6/5×6/7×8/7×8/9…)=4(1-1/9)(1-1/25)(1-1/49)(1-1/81)…
躺著背、坐著背、趴著背,還是 π 最好背!
由於大家都為 π 所著迷(一部分是為了測試超級電腦的速度和準確性),所以 π 曾經被算到幾兆位數。當然,其實我們並不需要這種精確度,只要知道 π 的前四十位數,你就可以測量出已知宇宙的周長,誤差不超過氫原子的半徑!
π 這個數已經發展到近乎讓人狂熱崇拜的地步了。許多人喜歡在「π 日」(3 月 14 日,用數字來呈現就是 3/14,剛好也是愛因斯坦的生日)讚頌 π。

在這一天,典型的活動可能包含展示和食用以數學為裝飾主題的派、打扮成愛因斯坦的樣子,當然也少不了 π 的記憶大賽。參賽的學生一般都可以記住 π 的幾十位數,但通常贏家都是那些記得超過一百位數的人。
對了,目前記憶 π 的世界紀錄是呂超這位中國人,他曾在 2005 年背誦出了 π 的 67,890 位數!根據《金氏世界紀錄》,呂超花了四年才記住這麼多位數,他也花了整整一天多的時間才將這些位數統統背誦出來。我們來看看 π 的前一百位數:
π = 3.141592653589793238462643383279502884197169399375105
820974944592307816406286208998628034825342117067 …
經過這麼多年,人們早已想出一些背誦圓周率的妙方,其中之一就是創造特殊的英文句子,讓句子裡每個單字所包含的字母數代表 π 的下一位數。一些著名的例子包括:
「How I wish I could calculate pi.」(得到七位數:3.141592)
「How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.」(提供了十五位數)

- (譯注:而在中文裡,有人用諧音的方式將圓周率藏在詩句中,其中最著名的是〈山巔〉這首五言絕句:「一寺一壺酒,二柳舞扇舞,把酒棄舊山,惡善百世流。」連題目共得到二十一位數:3.14159265358979323846。)
最令人佩服的例子出現在 1995 年,凱斯(Mike Keith)利用愛倫坡一首鬼斧神工的打油詩〈烏鴉〉創造出記住 740 位數的方法。這首詩的標題和第一節加起來就能產生出 42 位數,其中由十個字母組成的單字對應數字 0。
Poe, E. Near a Raven(譯注:對應 3.1415,以下依此類推)
Midnights so dreary, tired and weary.
Silently pondering volumes extolling all by-now obsolete lore.
During my rather long nap−the weirdest tap!
An ominous vibrating sound disturbing my chamber’s antedoor.
“This,” I whispered quietly, “I ignore.”
凱斯隨後將這首鉅作繼續延伸,寫出一首藏有 3835 位數的詩,題為〈Cadaeic Cadenza〉。(請注意,如果你用數字 3 代替字母 C、用 1 代替 A、用 4 代替 D……,那麼「cadaeic」這個字就會變成 3141593。)這首詩的開頭取材自〈烏鴉〉,但也包含了一些數位作品評論以及模仿其他詩詞的部分,比如說卡羅(Lewis Carroll)的詩作〈無聊〉(Jabberwocky)也在其中。
凱斯在這方面最新的貢獻是出版了一本書,書名是「Not a Wake: A Dream Embodying π’s Digits Fully for 10000 Decimals.」(請注意此書標題中每個單字的字母數!)這種用字母數來記憶 π 的方法有一個很大的問題,那就是即使你能記住這些句子、詩詞和故事,要立刻判斷出每個單字有多少字母也並非一件簡單的事。
關於這點,我喜歡的說法是:「多麼希望能跟大家解釋,其實通常有更好的記憶法可用。」( 「How I wish I could elucidate to others. There are often superior mnemonics!」這句話產生出13位數。)

來點音碼巧思,讓數字成為你朋友
要記住許多數字,我最喜歡用的方法是一種名為主要系統的音碼。在這套音碼中,每個數字都用一個或多個子音來表示。更具體地說:
1=t 或d
2=n
3=m
4=r
5=l
6=j、ch 或 sh
7=k 或硬 g 音
8=f 或 v
9=p 或 b
0=s 或 z
甚至還有人發明了幫你記住這套記憶系統的記憶法呢!我的朋友馬洛斯科維普(Tony Marloshkovips)提供了下列建議:字母 t(或發音相似的 d)中藏有一條直線;n 有兩條;m 有三條;而愛地球就別忘了環保 4R。伸出 5 根手指頭,你就會在拇指和食指之間看到 L;將 6 倒過來,看起來就很像字母 j;而兩個 7 可以組成一個K。(微軟系統)開機時按下 F8 能進入安全模式;將 9 左右或上下翻轉,就能得到 p 或 b。最後,ZO 就是 0 輸出的意思。
或者你也可以將這些子音統統照順序排好,形成TNMRLShKVPS,然後就會得到一個我(想像中的)朋友的名字:
Tony Marloshkovips
我們只要在每個相連的子音中插入母音,就能利用這套音碼讓數字變成文字。舉例來說,31 用到的子音有 m 和 t(或是 m 和 d),因此這個數字可以轉化成如下一些單字:
31 = mate, mute, mud, mad, maid, mitt, might, omit, muddy
請注意,像是「muddy」或是「mitt」這樣的單字是可以被接受的,因為 d 和 t 聽起來像是只出現一次,拼法也不會造成任何影響。此外,因為像是 h、w 和 y 這樣的子音並沒有出現在上表中,所以這些字母也能像母音一樣自由使用。因此我們可以將 31 轉化成像是「humid」或是「midway」這樣的單字。請注意,雖然同一個數字通常可以對應許多不同的單字,但是一個單字只能表示唯一的數字。
π 的前三個位數包含子音 m、t 和 r,這三位數可以轉換成如下一些單字:314 = meter, motor, metro, mutter, meteor, midyear, amateur;前五個位數 31415 可以變成「my turtle」這個詞。若再繼續延伸至 π 的前二十四位數,314159265358979323846264 就可以變成:
My turtle Pancho will, my love, pick up my new mover Ginger
然後將接下來的十七位數 33832795028841971 變成:My movie monkey plays in a favorite bucket;我很喜歡接下來的十九位數:6939937510582097494,因為它們可以對應一些較長的單字:Ship my puppy Michael to Sullivan’s backrubber;而下面十八個位數 459230781640628620 可以帶給我們這句話:A really open music video cheers Jenny F. Jones;然後再接下來的二十二位數 8998628034825342117067 則是:Have a baby fish knife so Marvin will marinate the goose chick!
於是,我們就將圓周率的前一百位數悄悄藏在這五個傻裡傻氣的句子中了!音碼對於記憶日期、電話號碼、信用卡號等長串數字都相當有用。試試看,只要稍加練習,你就能大大增強記住許多數字的能力了。
π 還是 τ?今天要算哪一道?請選擇!
π 是數學中最重要的數之一,這一點所有的數學家都會認同。但是如果你看看那些用到 π 的公式,你會發現它們大多會將 π 乘上 2。我們用希臘字母 τ(發音類似「陶」)來代表這個數。
τ = 2π
許多人相信如果我們能回到過去,就能因為用 τ 取代 π,而讓許多數學公式以及三角學中的關鍵概念變得比較簡單。在一些文章中,比如說帕萊(Bob Palais)的〈 π 是錯誤的!〉以及哈特爾(Michael Hartl)的〈 τ 的宣言〉,作者都優雅又饒富趣味地表達過這個想法。
這個論述的「中心點」在於圓都是由半徑來定義的,當我們將圓周和半徑相比的時候,就會得到 C/r=2π = τ。有些教科書現在會標示「兼容 τ」來表示這本書同時用 π 和 τ 來寫出公式。(雖然全面改用 τ 不會是輕鬆的過程,但許多學生和老師都認為使用 τ 會比 π 更輕鬆。)觀察這項行動在未來數十年會演變成什麼樣子是相當有趣的。
τ 的支持者(他們自稱為陶幫)誠摯地相信真理站在他們那邊,但他們也能包容比較傳統的符號。如同他們所說的,陶幫絕非頑固不化。下面是 τ 的前一百位數,其中插入了一些空格,對應我們隨後會提到的記憶法。請注意,τ 的開頭是 6,接著是 28,這兩個數目都是第六章提過的「完全數」。這是個巧合嗎?當然囉!不過還算是個有趣的花絮啦。
τ = 6.283185 30717958 64769252 867665 5900576 839433 8798750
211641949 8891846 15632 812572417 99725606 9650684 234135 ⋯
2012 年,當時才十三歲的布朗(Ethan Brown)締造了一項世界紀錄。為了一個募款計畫,他背出了 τ 的 2012 位數。他也是利用音碼,但並非創造出長句,而是創造出視覺圖像。每個畫面都包括了一個主體、一個動作(結尾永遠是現在進行式的 -ing)和一個當作受詞的物體。例如 τ 的前七位數:62 831 85 就變成「An ocean vomiting a waffle」(大海吐出一塊鬆餅)。下面是他為 τ 的前一百位數所創造出來的畫面:
An ocean vomiting a waffle
A mask tugging on a bailiff
A shark chopping nylon
Fudge coaching a cello
Elbows selling a couch
Foam burying a mummy
Fog paving glass
A handout shredding a prop
FIFA beautifying the Irish
A doll shooing a minnow
A photon looking neurotic
A puppy acknowledging the sewage
A peach losing its chauffeur
Honey marrying oatmeal
為了更容易記住這些畫面,布朗採用記憶宮殿這個方法。他想像自己在學校中遊蕩,當他沿著某條走廊前進並進入一間間的教室,每間教室裡都會有三到五個主體做著一些蠢事。最後,他得到了分布在 60 個地方的 272 個圖像。花了四個月準備之後,他用了 73 分鐘背誦出那 2012 位數。
來首餘韻無窮的 π 之歌吧!
讓我們用一首讚頌 π 的樂曲來結束這一章吧。這是我根據雷斯(Larry Lesser)的模仿歌曲〈美國 π〉(American Pi)所寫的一段新歌詞(譯著:雷斯所模仿的對象是〈American Pie〉這首經典歌曲)。這首歌你應該只唱一次就好,因為 π 是不會自我重複的。
很久,很久以前,
我還記得數學課總是讓我打瞌睡。
因為我們碰上的每一個數,
不是有終點就是一直重複。
但或許這世上其實有更厲害的數
但後來我的老師說:「給你一個挑戰,
試著找出圓的面積。」
雖然我嘗試無數,
我還是找不出一個分數。
我不記得我是不是哭了,
愈是嘗試或限制範圍,
但在我心深處有個東西觸動了我
就在這一天我認識了 π!
π 啊 π,數學上的 π,
兩個十一除以七是個不錯的嘗試。
你或許希望能提出一個美好的分數
但它的小數展開永不止息,
小數展開永不止息。
π 啊 π,數學上的 π,
3.141592653589。
你或許希望能用一個美好的分數來定義它,
但是小數展開永不止息!
本文摘自《數學大觀念:從數字到微積分,全面理解數學的 12 大觀念》,貓頭鷹出版。