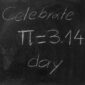- 作者/Steven Strogatz,本文摘自《無限的力量》,旗標出版,2020 年 09 月 09 日
崛起於東方的代數學
雖然微積分的確是在歐洲達到頂峰,但這支數學的根基其實是從別的地方開始的。比如說代數學,它起源於亞洲和中東地區。代數的英文名稱來自於阿拉伯文 al-jabr,原意為「修復」或「碎片重聚」,這是在平衡一道方程式並求解時所需的操作。舉例而言,在處理方程式時,我們經常將一個數字從等號的某一邊移除並加到另一邊,這便是一種先將方程式的一部分拆下再重新修復的過程。
另外,如同我們之前提過的,幾何學事實上源自於埃及。據傳,希臘的幾何學之父泰利斯(Thales)便是在埃及學到這門學問的。還有,幾何學中最著名的一個理論——「畢氏定理」實際上也不是畢達哥拉斯首先發現的;早在公元前 1800 年前的美索不達米亞泥板上就已經存在,證明巴比倫人知道這個定理的時間點比畢達哥拉斯早了至少一千年。

同時必須要注意的是,當我們提到古希臘時,其實是指一個遠超過雅典(Athens)和斯巴達(Sparta)的超廣大領土。在面積最遼闊的時候,它的南方邊界延伸到了埃及、西至義大利與西西里島、而東邊更是橫跨了地中海至土耳其、中東、中亞、甚至是部分的巴基斯坦與印度。畢達哥拉斯是在薩摩斯島(Samos)出生的,這是一座位於安納托利亞(Asia Minor;屬於今日的土耳其)西部海岸線之外的島嶼。阿基米德生活於敘拉古,它位在西西里島的東南方。而歐幾里得則在亞歷山大城附近活動,這是一座位於埃及尼羅河口的巨大港口,並且是當時的學術重鎮。
但在羅馬攻佔了希臘,特別是當位於亞歷山大城的圖書館被燒毀,以及西羅馬帝國隕落以後,數學研究的中心就又回到了東方。阿基米德、歐幾里得、托勒密、亞里斯多德和柏拉圖的作品都被翻譯成了阿拉伯文,並且被當時的學者和抄寫員流傳了下來。這些人同時也在過去的理論中添加了許多嶄新的想法。
代數如何興起,幾何又為何衰落?
在代數降臨前的幾個世紀,幾何學的進展就已經陷入了龜速慢爬時期。在阿基米德於公元前 212 年去世以後,似乎就沒有人能在這個領域超越他的成就。喔,抱歉,應該說「幾乎」沒有人可以超越。大約在公元 250 年,中國的幾何學者劉徽對阿基米德計算圓周率的方法做了改良。兩個世紀以後,祖沖之(公元 429 – 500 年,南北朝時代)使用劉徽的方法及一個 24,576 條邊的多邊形做計算,並在經過一段想必非常史詩級的算術處理後,成功將 π 值限制在以下的兩個數字之間:
3.1415926 < π < 3.1415927

又過了五個世紀,進步再度來臨,這一次是由一位名為哈桑‧本‧海什木(Al-Hasan Ibn al-Haytham;在歐洲通常寫作 Alhazen)的人完成。他於約公元 965 年時出生在伊拉克(Iraq)的巴斯拉(Basra),在進入伊斯蘭黃金時代後,他來到開羅(Cairo)從事包括神學、哲學、天文、醫學等各式各樣的研究。在海什木的幾何著作中,他思考一種阿基米德從未想過的立體圖形,並嘗試計算它的面積。與這個發現本身同樣令人吃驚的是,關於幾何學的重大進展也就這些了,且中間竟然花了十二個世紀的時間。
而就在這段時間裡,代數與算術正在經歷快速且重大的發展。來自印度的數學家發明了「零」這個概念,並創造了十進制系統。另外,關於如何解方程式的代數技巧也在埃及、伊拉克、波斯和中國遍地開花。這些進展大多源自於解決真實世界中的問題,例如:遺產繼承規則、納稅評估、商業活動、計帳、利息計算、以及其它可能用到數字與方程式的主題。

代數在當時仍是用文字敘述,也因此這些問題的解決方法都被寫成類似處方箋一樣的東西,上面包含了如何一步步得到答案的文字指引。其中一本著名的教科書是由穆罕默德‧伊本‧穆薩‧花拉子米(Muhammad Ibn Musa al-Khwarizmi;公元 780 – 850 年)所編寫的,因此作者的姓氏被用來泛指所有透過一系列步驟達成目的的程序,也就是演算法(algorithm,即 al-Khwarizmi 的拉丁文譯名)這個字的由來。最終,貿易商和探險家把這種以文字敘述為基礎的代數、以及從印度與阿拉伯發源的十進制帶往了歐洲,與此同時,人們也開始將阿拉伯文的文獻轉譯成拉丁文。
到了文藝復興時期的歐洲,除了應用層面的探索以外,將代數學符號化的研究也開始盛行起來,並且在 1500 年代達到頂峰。於是,方程式的樣貌開始類似於我們現今看到的樣子,也就是用字母來取代數字的形式。1591 年時,法國的弗朗索瓦‧韋達(François Viète)以母音字母(如:A 和 E)來代表未知值,並用子音字母(如:B 和 G)來代表常數。而如今我們用 x、y、z 表示未知值;a、b、c 表示常數的的習慣則源自於約五十年後出現的笛卡兒。這種使用符號與字母來取代文字敘述的作法,使得方程式的推導與求解更為容易。
在算術上也有同樣重大的突破,那就是來自荷蘭的西蒙‧斯蒂文(Simon Stevin)將阿拉伯十進制數字從整數擴大運用到了小數上,並藉此成功消除了亞里斯多德思想中關於數字(即今天的整數,兩相鄰整數間沒有更小的單位存在)與大小(一種連續的數量,可以被分割成無限小的單位)之間的差異。

在斯蒂文以前,十進制只適用於整數上,而任何小於一單位的數就用分數來表示;但在斯蒂文的新方法中,一個單位的整數可被切割成更小的單位,也就是小數。這對於今天的我們來說是理所當然的事,但在那時卻是一項革命性的想法。當整數具有可分割性,則整數、分數或無理數便可以被整合到一個被稱為「實數」的大家庭中,這給了微積分描述連續空間、時間、運動與變化一項強大而必需的工具。
就在幾何學即將與代數合而為一的前夕,阿基米德所用的舊幾何學方法還有最後一次成功的應用:克卜勒將帶有弧度的物體(如:酒桶和甜甜圈形狀的物體)在腦中切成無限多片且無限薄的圓盤,並藉此計算它們的體積;另外,伽利略與他的學生埃萬傑利斯塔‧托里切利(Evangelista Torricelli)、博納文圖拉‧卡瓦列里(Bonaventura Cavalieri)也是透過將物體視為無限多條線或面的堆疊來求得面積、體積或重心。
然而,這些人在對待「無限大」或「無限小」的概念時可以說是漫不經心,因此他們的方法雖然有力且直覺,卻一點兒也不嚴謹。儘管如此,由於這些方法能比窮盡法更容易且更快速地找到答案,所以也不失為一項讓人感到興奮的進步(當然,如今我們已經知道阿基米德早就使用過這種技巧了,他在關於「方法」的論述裡早就提過相同的點子,只不過當時這些敘述被深埋在一本收藏於修道院的祈禱書之中,直到 1899 年才被人發現)。
無論如何,雖然那些新阿基米德派的做法在當時看上去相當有效,但它們卻不足以應付未來的挑戰。而符號代數此時已經蓄勢待發,與之相關的兩支強大分支,即解析幾何與微分,也已如春芽一般呼之欲出。