傳奇的「數學王子」高斯 │ 科學史上的今天：3/30

本文與 PAMO車禍線上律師 合作，泛科學企劃執行

走在台灣的街頭，你是否發現馬路變得越來越「急躁」？滿街穿梭的外送員、分秒必爭的多元計程車，為了拚單量與獎金，每個人都在跟時間賽跑 。與此同時，拜經濟發展所賜，路上的豪車也變多了 。

這場關於速度與金錢的博弈，讓車禍不再只是一場意外，更是一場複雜的經濟算計。PAMO 車禍線上律師施尚宏律師在接受《思想實驗室 video podcast》訪談時指出，我們正處於一個交通生態的轉折點，當「把車當生財工具」的職業駕駛，撞上了「將車視為珍貴資產」的豪車車主，傳統的理賠邏輯往往會失靈 。

在「停工即停薪」（有跑才有錢，沒跑就沒收入）的零工經濟時代，如果運氣不好遇上車禍，我們該如何證明自己的時間價值？又該如何在保險無法覆蓋的灰色地帶中全身而退？

薪資證明的難題：零工經濟者的「隱形損失」

過去處理車禍理賠，邏輯相對單純：拿出公司的薪資單或扣繳憑單，計算這幾個月的平均薪資，就能算出因傷停工的「薪資損失」。

但在零工經濟時代，這套邏輯卡關了！施尚宏律師指出，許多外送員、自由接案者或是工地打工者，他們的收入往往是領現金，或者分散在多個不同的 App 平台中 。更麻煩的是，零工經濟的特性是「高度變動」，上個月可能拚了 7 萬，這個月休息可能只有 0 元，導致「平均收入」難以定義 。

這時候，律師的角色就不只是法條的背誦者，更像是一名「翻譯」。

施律師解釋「PAMO車禍線上律師的工作是把外送員口中零散的『跑單損失』，轉譯成法官或保險公司聽得懂的法律語言。」 這包括將不同平台（如 Uber、台灣大車隊）的流水帳整合，或是找出過往的接單紀錄來證明當事人的「勞動能力」。即使當下沒有收入（例如學生開學期間），只要能證明過往的接單能力與紀錄，在談判桌上就有籌碼要求合理的「勞動力減損賠償 」。

300 萬張罰單背後的僥倖：你的直覺，正在害死你

根據警政署統計，台灣交通違規的第一名常年是「違規停車」，一年可以開出約 300 萬張罰單 。這龐大的數字背後，藏著兩個台灣駕駛人最容易誤判的「直覺陷阱」。

陷阱 A：我在紅線違停，人還在車上，沒撞到也要負責？ 許多人認為：「我人就在車上，車子也沒動，甚至是熄火狀態。結果一台機車為了閃避我，自己操作不當摔倒了，這關我什麼事？」

施律師警告，這是一個致命的陷阱。「人在車上」或「車子沒動」在法律上並不是免死金牌 。法律看重的是「因果關係」。只要你的違停行為阻礙了視線或壓縮了車道，導致後方車輛必須閃避而發生事故，你就可能必須背負民事賠償責任，甚至揹上「過失傷害」的刑責 。 

數據會說話： 台灣每年約有 700 件車禍是直接因違規停車導致的 。這 300 萬張罰單背後的僥倖心態，其巨大的代價可能是人命。

陷阱 B：變換車道沒擦撞，對方自己嚇到摔車也算我的？ 另一個常年霸榜的肇事原因是「變換車道不當」 。如果你切換車道時，後方騎士因為嚇到而摔車，但你感覺車身「沒震動、沒碰撞」，能不能直接開走？

答案是：絕對不行。

施律師強調，車禍不以「碰撞」為前提 。只要你的駕駛行為與對方的事故有因果關係，你若直接離開現場，在法律上就構成了「肇事逃逸」。這是一條公訴罪，後果遠比你想像的嚴重。正確的做法永遠是：停下來報警，釐清責任，並保留行車記錄器自保 。

保險不夠賠？豪車時代的「超額算計」

另一個現代駕駛的惡夢，是撞到豪車。這不僅是因為修車費貴，更因為衍生出的「代步費用」驚人。

施律師舉例，過去撞到車，只要把車修好就沒事。但現在如果撞到一台 BMW 320，車主可能會主張修車的 8 天期間，他需要租一台同等級的 BMW 320 來代步 。以一天租金 4000 元計算，光是代步費就多了 3 萬多塊 。這時候，一般人會發現「全險」竟然不夠用。為什麼？

因為保險公司承擔的是「合理的賠償責任」，他們有內部的數據庫，只願意賠償一般行情的修車費或代步費 。但對方車主可能不這麼想，為了拿到這筆額外的錢，對方可能會採取「以刑逼民」的策略：提告過失傷害，利用刑事訴訟的壓力（背上前科的恐懼），迫使你自掏腰包補足保險公司不願賠償的差額 。

這就是為什麼在全險之外，駕駛人仍需要懂得談判策略，或考慮尋求律師協助，在保險公司與對方的漫天喊價之間，找到一個停損點 。

談判桌的最佳姿態：「溫柔而堅定」最有效？

除了有單據的財損，車禍中最難談判的往往是「精神慰撫金」。施律師直言，這在法律上沒有公式，甚至有點像「開獎」，高度依賴法官的自由心證 。

雖然保險公司內部有一套簡單的算法（例如醫療費用的 2 到 5 倍），但到了法院，法官會考量雙方的社會地位、傷勢嚴重程度 。在缺乏標準公式的情況下，正確的「態度」能幫您起到加分效果。

施律師建議，在談判桌上最好的姿態是「溫柔而堅定」。有些人會試圖「扮窮」或「裝兇」，這通常會有反效果。特別是面對看過無數案件的保險理賠員，裝兇只會讓對方心裡想著：「進了法院我保證你一毛都拿不到，準備看你笑話」。

相反地，如果你能客氣地溝通，但手中握有完整的接單紀錄、醫療單據，清楚知道自己的底線與權益，這種「堅定」反而能讓談判對手買單，甚至在證明不足的情況下（如外送員的開學期間收入），更願意採信你的主張 。

車禍不只是一場意外，它是認知、情緒、金錢與法律邏輯的總和 。

在這個交通環境日益複雜的時代，無論你是為了生計奔波的職業駕駛，還是天天上路的通勤族，光靠保險或許已經不夠。大部分的車禍其實都是小案子，可能只是賠償 2000 元的輕微擦撞，或是責任不明的糾紛。為了這點錢，要花幾萬塊請律師打官司絕對「不划算」。但當事人往往會因為資訊落差，恐懼於「會不會被告肇逃？」、「會不會留案底？」、「賠償多少才合理？」而整夜睡不著覺 。

PAMO看準了這個「焦慮商機」， 推出了一種顛覆傳統的解決方案——「年費 1200 元的訂閱制法律服務 」。

這就像是「法律界的 Netflix」或「汽車強制險」的概念。PAMO 的核心邏輯不是「代打」，而是「賦能」。不同於傳統律師收費高昂，PAMO 提倡的是「大腦武裝」，當車禍發生時，線上律師團提供策略，教你怎麼做筆錄、怎麼蒐證、怎麼判斷對方開價合不合理等。

施律師表示，他們的目標是讓客戶在面對不確定的風險時，背後有個軍師，能安心地睡個好覺 。平時保留好收入證明、發生事故時懂得不亂說話、與各方談判時掌握對應策略 。

從違停的陷阱到訂閱制的解方，我們正處於交通與法律的轉型期。未來，挑戰將更加嚴峻。

當 AI 與自駕車（Level 4/5）真正上路，一旦發生事故，責任主體將從「駕駛人」轉向「車廠」或「演算法系統」 。屆時，誰該負責？怎麼舉證？

但在那天來臨之前，面對馬路上的豪車、零工騎士與法律陷阱，你選擇相信運氣，還是相信策略？ 先「武裝好自己的大腦」，或許才是現代駕駛人最明智的保險。

PAMO車禍線上律師官網：https://pse.is/8juv6k 

最近在網路上看到一波針對星座的熱切討論，講得更精確點，是關於某位知名人士對「風象星座有人格瑕疵」的論述引起的風波。身為一個 AB 型天蠍座戰車心理學專業，肯定是要跳出來發表一點個人意見。

這類與人格特質有關的命理占卜，不管是血型、星座還是塔羅，在心理學界一直都是充滿討論熱度的命題。相關研究為數不少，但結果總是差強人意，或沒辦法說服另一方的支持者。但如果單從邏輯推論的角度出發，倒也有不少可以說出來引發思考的東西。

這裡先不討論在占卜或這類神秘學常見的「巴南效應」（感興趣的朋友可以自行 Google，絕對能找到一卡車的文章或懶人包），我比較想討論的是人格特質本身的各種「意義」，以及我們應該用怎樣的角度看待。

（為了避免不必要的爭議，以下內容只是我的看法。如果你覺得這個論調有趣，不妨跟自己原本的想法比較；如果你覺得我說的是錯的，也歡迎提出你的看法與相應的依據。畢竟這個領域的東西至今仍未有定論，你我都有可能是錯的，又說不定我們都是對的，誰知道呢？）

你熱情，我冷漠？人格真的這麼說一不二嗎？

人格特質是什麼？不同流派、學說的擁戴者都有各自的說法，但是普遍來說，心理學界傾向把它視為一套「具辨識度的認知、行為與情感模式」。換言之，就是個體在特定情境中會「怎麼思考」、「怎麼行動」與「怎麼感受」的傾向（劃重點）。

人格特質並不是一個全有全無的開關、更沒有所謂「絕對值」存在，它只是種描述性的「比較」用語。例如，「易怒」者必須跟情緒控管能力較好的人相比才能體現「內向」者也得放在「外向」的人身邊，才能看出差異，每個人格特質都在描述你跟常模（norm）之間的差異。

這也是當前社會大眾對人格特質常有的誤解。不管是「內向 vs. 外向」、「固執 vs. 隨和」，人格特質都不是像我們打遊戲點能力值，或是煮菜時往鍋子裡加調味料那樣容易量化。它更像是一段連續的「光譜」，就連你在人格測驗裡得到的任何結果都只是相對值，而非絕對值。

舉個實例。最常被運用在各種地方的 Big 5 人格特質模型，由開放性（openness）、嚴謹性（conscientiousness）、外向性（extroversion）、親和性（agreeableness）、情緒不穩定性（neuroticism）5種傾向構成。但是今天就算你在情緒不穩定性的測驗拿了 0 分，也只代表你比絕大多數人還要不容易情緒失控、陷入焦慮或其他負面情緒，而不是「絕對不會」有這些反應。

說得極端一點，如果今天有人「完全沒有」某種反應能力（例如完全不會生氣、不會感到恐懼，或是完全沒有攻擊性），那他反而會因為心智功能的缺損成為臨床上的「異常」。

當然，這些都是比較嚴謹的學術定義。日常的人際互動不是在寫論文，標準放得寬鬆一些也很正常。但問題就在於這個「標準」到底從何而來，又有怎樣的問題？

常態分配告訴我們的事：總會有人剛好是那五成

前面提到了人格特質是跟「常模」比較之後得出的結果，提到統計了，就再討論一個「常態分配」（normal distribution）概念吧。

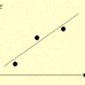
「常態分配」是自然科學與社會科學常用的統計模型，也就是在面對一個實際狀況不明或無法觀測的變項時，以樣本平均數為中心去做的連續機率分佈假設。

簡而言之，只要人格測驗的樣本數大到一定程度且沒有偏斜（例如外力干擾或測量失誤）的前提下，測驗分數的分佈應該會接近下面這樣：

這張常態分配圖表就是前面所說的「常模」，也是母群在我們的假設中的模樣，有 50% 的人大於等於平均值，同時也有 50% 的人小於等於平均值。

在認識常態分配代表的意義後，再來看「天蠍座就是愛記仇」、「處女座就是龜毛」、「Ｂ 型人就是散漫」、「天馬座就得會流星拳」之類帶有二元對立性質的判斷句，是否就能品嚐出一點微妙的不協調了？

因為任何一個人格特質中，至少會有 50% 的人高於平均值、落入「符合描述」的區間。這 50% 的人口比例對比 12 分之 1 的星座人口分佈，很明顯是絕對「塞不下」的。（我知道每個星座的出生人口並不是那麼平均，但比例也沒有懸殊到可以把這個 50% 合理消化。）

如果我們把條件放得再寬鬆一點，把符合描述的條件改成「會有相應外顯行為」即可，那即便只算 1 個標準差以內的範圍，符合描述的人口比例也會來到驚人的 85%。

但是很顯然，這個數據並不符合我們在日常生活感受到的「現實」，一方面是因為，實際的人格特質分佈會受到時空背景、在地文化、社經發展等錯綜複雜因素的影響，例如隨著網路與智慧型裝置的出現，新生代就明顯比老一輩的人表現出更高的經驗開放性，又或者都市人口的情緒不穩定性會高過鄉村等。

另一方面，是因為我們對他人（甚至是自己）的人格評價，很多時候並不是這麼「客觀」。

不是只有天蠍座會記仇，而是天蠍座記仇才會被記住

人的大腦畢竟不是一張 Excel 報表，相比起「平均值」、「絕對值」一類的量化資訊，我們對他人的（甚至是自己）的評價更容易受到「代表性」或其他質性因素影響。

一個曾經說謊被當面拆穿的人，就算他平常都為人誠懇，你依然會在心中對這人打上「不老實」、「不可靠」的記號；一隻曾經把你手抓傷的貓，不管主人再怎麼誇獎，你還是會有「牠很兇」的陰影。特別是對不熟的人事物來說，正因為這些「偶發事件」太過突兀，反而會在心中留下深刻的印象。

這也是為什麼最廣為流傳的命理占卜，往往會是「負面內容」。因為相比起「友善」、「隨和」、「體貼」這些有助於促進人際和諧的特質，「愛紀仇」、「自我中心」、「控制欲強」等會造成衝突的「瑕疵」更具代表性，進而成為這些星座或血型的原罪。

一旦刻板印象形成，就會反過來篩選我們接觸到的刺激。戴上這副有色眼鏡後，大腦便會開始把跟框架相符的資訊保留下來，當成強化刻板印象的建材，其他不相符的資訊不是被忽略、就是以「特例」的形式保留下來。

一來一往下，「我知道不是每個 OO 座的人都這樣，但我身邊的 OO 座真的就是 XX」的偏差認知就會深深紮根在我們的腦中、再難剔除。

這些基於代表性而產生的判斷，其實都只是片面、不完整的觀測。雖然經過無數人的努力研究，我們至今也沒辦法定論——天象或血型這些自然現象是否真的存在某些超乎想像的影響？也很難設計出令人信服又符合倫理的實徵實驗；但至少在「人格特質」這個面向上，我們都不是寥寥幾個形容詞就能概括的。

每個人都有獨特之處，這些「特點」並非一成不變，就好像再鋼鐵的直男也會因為天竺鼠車車冒出粉紅色泡泡（？）。我們就像一塊未經雕琢的水晶，每個角度都能在燈光下折射出不同層次的光斑。或許正是因為這些光斑太過駁雜，才讓我們總想著用能理解的框架去解釋與限制它的變化。

把星座、血型、生命靈數等先天條件跟人格特質結合，這是人類社會無數年發展下來很「正常」的現象。不管科學也好、神秘學也罷，都只是在用自己的方式追尋那虛無縹緲的「真理」。

在大家目標一致的前提下，最怕的從來就不是歧異或討論，而是先入為主的想法，讓我們忽略了自己本有的無限可能性。因為一旦你把窗戶關死，久了可是會連外頭世界有多寬廣都全然忘掉。

參考資料：

1. Cervone, D., & Pervin, L. A. (2015). Personality: Theory and research. John Wiley & Sons.
2. Howell, D. C. (2012). Statistical methods for psychology. Cengage Learning.
3. John, O. P., & Srivastava, S. (1999). The Big Five trait taxonomy: History, measurement, and theoretical perspectives. Handbook of personality: Theory and research, 2(1999), 102-138.

三種機率型態中，最為人熟悉的莫過於兩個世紀前崛起的鐘形分布／常態分布。打從一開始，常態分布的理論就十分有影響力且頗具爭議。確實，常態分布的發明還有一段為人津津樂道的故事，那就是法國數學家勒讓德（Adrien-Marie Legendre, 1752-1833）和史上最有名的數學家高斯之間的爭論。

十九世紀初，計算天體運行軌道是當時數學研究中走在尖端的一個領域。日新月異的望遠鏡為科學家帶來更多天體的新資訊，而牛頓的地心引力定律，更是科學家用以分析觀測數據的利器。

不過，早在十六世紀末，著名丹麥天文學家第谷．布拉赫（Tycho Brahe, 1546-1601）所處的年代，人們就知道天文觀測很容易有誤差。首先，望遠鏡本身就有瑕疵：鏡片打磨效果不佳，而且底座不平。儀器方面的誤差還可以衡量、補救，但其他方面的狀況就很難控制了，例如大氣的狀態、地球的震動，以及喝醉酒的天文台助理。諸如此類無法控制的差錯，都會嚴重影響新彗星或行星運行軌道的測量。

就跟從前多數的數學家一樣，勒讓德和高斯在專業方面的興趣相當廣泛。

在巴黎的勒讓德不但將歐幾里得著名的幾何學，重新編寫成該領域的標準教材，完成數論領域第一本專著，並且於拿破崙主政時期協助精準測量出巴黎地區的地圖。

身處德國北部漢諾瓦王國（漢諾瓦王朝曾經是好幾代的英國國王）的高斯則是個神童，工人子弟出身的他在牙牙學語之前就會算數了，十八歲便完成他第一個有名的幾何學證明。舉凡他碰過的領域，沒有一個不因而更加進步，例如質數、代數函數、無窮級數、機率及拓樸學。

高斯和同事共同設計了第一架電報機。跟勒讓德一樣，他也忙著勘測地圖。此外，高斯以極少的數據計算出數個新發現小行星的運行軌道。確實，高斯的運算速度恐怕鮮少有人比得上，他只花十個小時就計算出灶神星（Vesta）的軌道並加以驗證，換做是別人，可能要好幾天辛苦地計算、查證、核對。

這兩個人的衝突，就發生在天文學領域。

1806 年，勒讓德發表一篇論文探討天體運行軌道的計算，其中包括名為「論最小平方法」（On the method of least squares）的附錄。該篇論文主要是探討常見的難題：如何用誤差重重的觀測值，計算出運行軌道或其他自然現象的正確值。

方法很簡單，首先猜測軌道的正確值，計算該值與各個觀測值相差多少——這就是誤差。然後計算誤差的平方值，將之加總起來。接著，再猜測軌道的正確值，重複先前的步驟，看看誤差平方值之總和是否比上一次小。就這樣一再重複。最小平方法可以找出最小的誤差平方值總和，它就是最接近所有觀測值的數據。

這是很有效的方法，立刻被許多人採用，時至今日更被運用在各式物理研究上，從天文學到生物學無所不包。

但是，高斯沒有將勒讓德放在眼裡，在勒讓德提出該論文三年之後，他也發表類似的計算方法。勒讓德當然提出抗議。高斯向來不屑跟其他數學家爭辯，總覺得浪費時間。他沒有直接回應，只對同事表示他在十八歲時就發明這個方法了，而且已經在天文計算上用過很多次。拉普拉斯試圖居中協調，但沒有成功。

最後勒讓德和高斯兩人都被認可為最小平方法的發明人。後人企圖在高斯的手稿中尋找證明，結果雖仍有爭議，但比起勒讓德，高斯對最小平方法的了解顯然更為高段。

本文摘自《股價、棉花與尼羅河密碼》，早安財經文化出版。