讓唸書跟打電動一樣——專訪台大PaGamO幕後團隊！

什麼樣的臺灣自製線上遊戲，能讓四大報聯合報導，《科學人》、《今週刊》、《天下雜誌》紛紛採訪，甚至前進大陸還登上國際媒體？沒錯，就是風靡華人世界兩萬個大學生的免費線上遊戲PaGamO，讓你一邊玩一邊光明正大地說：「媽，我在唸書。」

而這個全球首創的線上遊戲學習系統，是由一群台大學生從頭架設的。

葉丙成教授在今年九月登上 TEDxTaipei，分享如何用線上遊戲翻轉教室，讓學生對解題上癮。在演講最後，老師激動地請共同開發線上遊戲PaGamO的蔣盛文、沈大鈞、陳彥霖、陳彥鈞、徐子函、朱柏澂、張耀仁、 余朗祺、夏誌陽、唐偉軒、李嘉玲、林冠宇還有蔡翼成上台，呈現了這樣一幅類海賊王的熱血團隊大合照。並笑著說 dress code 只有不能穿夾角拖。

葉丙成老師的機率課不但是第一批在大規模公開線上課程Coursera上推出的華語課程之一，PaGamO（台語：打Game學）更是全球首次放上 MOOCs 的線上遊戲學習系統，希望學生用玩遊戲的熱情來解機率題目。在媒體撲天蓋地的訪問報導下，葉丙成教授在 Facebook 上感嘆：「(因為Coursera)被不少媒體訪問。每次我都特別提到，我們幾位台大電機跟資訊的同學們跟我一起開發的 PaGamO 多人線上遊戲平台，將會是全球首創的把 MOOCs 與線上遊戲結合的新革命。……多麼希望能讓台灣知道我們也有這樣難得的年輕人。……唉，每次看到報導裡面沒有同學的名字，心裡就覺得很失落。」

於是默默follow葉老師的A編，就害羞地聯絡教授，希望能採訪這些一起寫出整個遊戲的大三大四學生。

雖然這次老師在 Coursera 的機率課已經結束了，但為了第二代的 PaGamO 以及後續的課程，葉老師和同學仍然一個禮拜開會兩次，繼續開發系統。葉老師也找了具有業界實務經驗的朋友擔任專案經理，調度工程進度，讓系統能更快上軌道，這也顯示團隊非常重視這套系統，並不是曇花一現就任其荒廢。

這次的採訪我們逮到了蔣盛文、陳彥霖和陳彥鈞三位同學。當初是怎麼加入這個遊戲開發團隊的？同學用「簡約表示式」答道：「我是他導生。」「我是老師的專題生。」「我和夏誌陽在麥當勞吃飯接到電話。」「老師找我們去丹堤談。」

原來葉老師早在 2012 年就有遊戲結合課程的想法，在寒假時決定付諸實行，於是從約吃飯、打電話，一一親自約談，串起這群熱血的同學。陳彥霖回憶那個寒假提到：「我們前兩個禮拜大概玩了十幾種網頁遊戲。」從體驗開始，瞭解網頁遊戲如何運作、怎樣讓玩家容易上手、如何能持續吸引玩家，再開始思考該如何設計一套遊戲。

雖然說這群資工系和電機系的同學，已經是寫程式的高手了，但是開發 PaGamO 用的是他們以前沒碰過的開源 Web 應用框架 Ruby on Rails，大家還是得重新摸索，幾乎每個人都說學寫新程式語言，是過程中最痛苦的事；第二痛苦的則是：一個禮拜吃三次麥當勞。反而暑假時一個禮拜三次、從下午一兩點寫 code 到半夜的經驗，沒那麼難熬。（或許熬夜 coding 是電機系和資工系學生的基本功）

至於整個開發最困難的地方，陳彥霖覺得是「合作」；畢竟大家都是學生，沒有太多合作一個大專題的經驗，工作分配的產生是「自然演替」的結果－起初，大家懂得都差不多，但是稍微擅長某項任務的同學就會較多擔當，自然而然也就將這份任務分配給他，後來團隊間大家比較瞭解誰擅長什麼，才開始有比較明確的分工。

PaGamO 的前身是台大電機系機率課中的 BJ online，是葉丙成教授和研究生姜哲雄討論的想法，讓修課同學能在遊戲裡互相出題、互相破解，激發大家解題的慾望。由於很成功很有趣，而想要搬到Coursera上讓全世界修課的學生一起參與。這代表的是從原本 72 人的網頁遊戲變成 2 萬人的連線對戰，不管是介面設計或是系統穩定度都要夠好，所以要重新設計重新寫。

精美的遊戲介面是繪師徐子函一個人自己完成。「他可說是最勞苦功高的。」也很可惜沒訪問到同學口中強大的大鈞：「（大鈞）他做的地圖和前台，到現在程式有些地方其他人還是看不懂。」

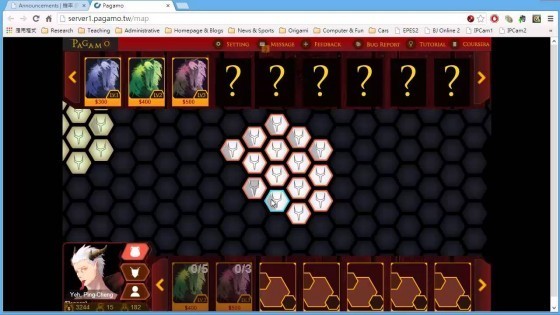
玩過很多遊戲的他們，該有的遊戲設計一點都不含糊，像是新手教學、選角色、地圖、賺錢買怪獸防守等等都有。開發的同學也很快樂地攻擊這個遊戲系統，找尋任何可能的程式漏洞，然後再把洞補起來，避免可能破壞遊戲公平性的作弊方式（刷外掛、DDoS 攻擊之類的）。

比較可惜的是，由於在一萬起跳的學生人數下，要想辦法審核修課學生出的題目有一定水準有點困難－總不能讓學生隨便出個「老師是帥哥的機率是多少？」這種答案太簡單(100%)的題目－因此在第一代的 PaGemO 中沒有開放給學生互出題目難倒對方。但要從哪弄來這麼多題目呢？最後是葉老師的研究生林冠宇，一個人拼出200題有創意又高品質的題目讓修課學生破關。

「那上線之後有出過什麼大問題嗎？」

同學倒是歪著頭想了很久，老半天才迸出一句說：「程式出現問題然後想辦法去解決是很正常的事。」比較嚴重的像是，資料庫結構曾經出現漏洞就整個掛掉，還有伺服器跑進無限迴圈當掉，只好緊急停機維修。之前期末為了要讓修課同學能夠像一般的大學生臨時抱佛腳，就把遊戲中每個玩家的體力（AP）都設定無上限，讓大家可以一直玩（之前體力會慢慢掉，會限定一段時間內只能解幾題、攻多少的地），結果就有人把別人殺得死無全屍—呃，我是說把地都佔光光了—最後團隊只好道歉，回溯六小時前的紀錄。

從寒假忙到現在，又可以預見地會繼續忙到明年寒假以後。除了葉老師的熱血號召之外，是什麼讓他們願意這樣盡心盡力？

有很誠實也很謙遜的回答：「因為想要有在大型專案 coding 的經驗。」或者：「因為 Coursera 這種大規模線上課程，可以讓世界各地的人，只要能上網、只要有時間、只要願意學都可以學習。是一個值得推動的理想。」

這套系統還不斷在精進，陳同學說：「第二代的 PaGamO 要能讓大家互相出題目，增加遊戲性和教育性，並且希望可以讓其他課程也能用這套遊戲系統。」

與此同時，其他比較晚到的同學已經開好筆電，批哩啪啦地敲起了鍵盤。我們匆匆跟同學道謝之後，一個學長馬上開了投影幕問他們進度，他們異口同聲的笑說：「這版本一定是舊的，我們已經改很多了。」，然後指著螢幕比手劃腳，一邊講著一堆專業術語，一邊轉回自己的筆電調檔案。

「You are my true heroes!! I am blessed to have the chance to work with you guys to make our dream come true!!」」葉丙成教授說：「我要讓世界看到這十二位難得的年輕人：蔣盛文、沈大鈞、陳彥霖、陳彥鈞、徐子函、朱柏澂、張耀仁、余朗祺、夏誌陽、唐偉軒、李嘉玲、林冠宇 and  蔡翼成兄」

附錄

• 葉丙成教授在TEDxTaipei上的演講：
  超越教育！線上學習新革命
• 果殼網的葉丙成教授專訪：
  台大葉丙成：用生命在賣萌的MOOC教育者
  葉丙成：修課如遊戲？台大電機這麼教！

幕後花絮：

Z編：好緊張喔，待會兒就要見到心目中的偶像了。
A編：你要簽名照嗎？我可以幫你照相。

結果我們最後還是沒有跟葉丙成教授照到相。（殘念）