文/黃誠熙(Sky Huang),目前為UCLA材料系博士候選人
在生活中我們常常洗東西:洗碗、洗杯子、洗衣服…等等,可是怎麼洗東西才最有效率呢?讓我們先來想像一下洗東西的過程中發生了甚麼事情:我們在容器中注入水,髒東西會溶解到水中形成水溶液;接著我們把水倒掉,此時雖然大部分的東西都進入了下水道,但仍有一部分的水溶液留在容器中,他們或許存在杯壁上(例如洗過後的杯子放置一陣子底部會累積杯壁上受重力吸引而滑落的水),或是洗衣服時殘留在衣服中怎樣也扭不乾,而這些水溶液就是我們無法洗淨東西的原因。
那到底要怎樣洗東西才會清潔溜溜又省水、省時間,有效率到讓 CP 值破表呢?
1.洗衣服要沖幾次水才會乾淨?-單次清洗的水量固定時,沖洗次數和殘留的關係
先來考慮洗衣服的情況。洗衣服時會先放入洗衣精洗淨衣物,接著再注入水把洗衣精沖掉。我們是否有時候會擔心洗衣精殘留呢?到底沖洗一次和兩次和三次殘留洗衣精的量的差別是什麼呢?
首先,先帶入一些變量:
- x:倒入的洗衣精的重量(克)
- W:裝滿洗衣機的水溶液的體積(公升)
- L:排水以後還殘餘的水溶液的體積(公升)
可以計算,洗過一次以後,剩餘的洗衣精的量是![]() 克。因為在此問題中,
克。因為在此問題中,![]() 為一個常數,因此我們帶入一個常數C=
為一個常數,因此我們帶入一個常數C=![]() 。則我們可以計算重複加水再排水這個步驟三次,殘餘的洗衣精的重量為xC3。因此,在洗滌n次之後,殘留洗衣精的關係式為:
。則我們可以計算重複加水再排水這個步驟三次,殘餘的洗衣精的重量為xC3。因此,在洗滌n次之後,殘留洗衣精的關係式為:
結論:殘餘的洗衣精會隨著清洗次數指數下降,假如C是0.1,那洗一次殘存10%,洗兩次殘存1%,洗三次殘存0.1%,以此類推。
2.手滑加了太多清潔劑怎麼辦?-固定的清洗過程,加入的清潔劑重量和殘留的關係
有的時候我們會不小心手滑加太多洗衣精,或是因為衣服比較髒而加入較多的洗衣精。這時候你可能會想,那之後會不會殘留大量的洗衣精而影響健康呢?
我們可以再次使用方程式(1)來了解這個問題。在這次的問題中,因為是固定清洗過程,所以洗衣機的水體積固定,排水後殘留在洗衣機和衣服中的水溶液體積固定,清洗次數也固定,因此,在方程式(1)後面的C為常數,殘留的洗衣精重量也就取決於一開始加入的洗衣精重量x。這意思是說,假設我們不小心手殘倒了兩倍的洗衣精進洗衣機裡,事實上最後衣服上殘留的洗衣精的量也只是正常沒有手殘的兩倍,似乎,好像也不用太擔心呢(?)
結論:殘留的洗衣精的量直接正比於一開始倒入洗衣機的重量

3.碗要怎麼洗會比較乾淨?-總水量固定時,清洗次數和殘留的關係
接著讓我們看看如何洗碗。想像有時候我們想要節省水,譬如出外露營,攜帶的水有限;又或是想節省時間,像是,一邊洗碗一邊發現電視中球賽快要開始了。這時我們就會想知道最有效率的洗碗法,可以洗得快又乾淨!因此,這邊想討論:在固定水量(假若水龍頭水流量固定,亦為固定時間)的情況下,哪一種方式洗滌會洗的最乾淨;是一次把水用完呢,還是分兩次但是每一次只有一半的水,或是分四次?是否有一個”魔法數字”可以得到最佳的洗滌效果呢?
推導過程如下:同樣令髒東西一開始有x克,我們可以使用的總水量是W公升,在分n次洗滌的情況下,每次倒入![]() 公升的水清洗器具後倒掉,進行n次,而每次倒掉之後殘餘的水溶液為L公升。我們先來看幾個例子;若是我們一次用完全部的水量W,則殘留髒東西的重量為
公升的水清洗器具後倒掉,進行n次,而每次倒掉之後殘餘的水溶液為L公升。我們先來看幾個例子;若是我們一次用完全部的水量W,則殘留髒東西的重量為![]() ;若是兩次用完,每次使用水量為
;若是兩次用完,每次使用水量為![]() ,則為
,則為![]() 。因此,我們可以寫下殘留的髒東西的量為:
。因此,我們可以寫下殘留的髒東西的量為:
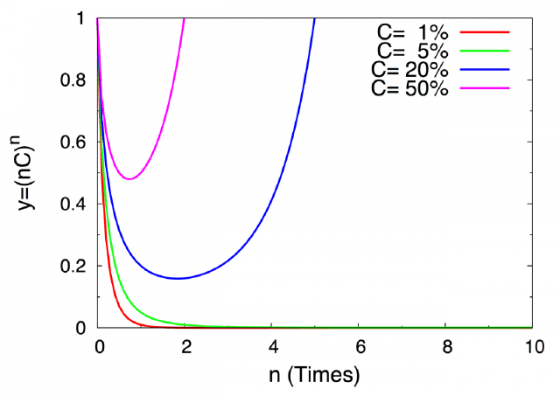
其中和上面一樣,為固定的值![]() ,我們把它令成常數C。我們想要知道的就是,甚麼樣的n可以讓y有最小值,但是這個方程式是個有點複雜的方程式,因此我們嘗試使用數值解(註2),也就是畫出y和n的關係式,使用肉眼來找出y的最小值。下圖是數個不同的C的值y隨著n的變化情況:
,我們把它令成常數C。我們想要知道的就是,甚麼樣的n可以讓y有最小值,但是這個方程式是個有點複雜的方程式,因此我們嘗試使用數值解(註2),也就是畫出y和n的關係式,使用肉眼來找出y的最小值。下圖是數個不同的C的值y隨著n的變化情況:
在這邊我只畫出合理的n的範圍(應該不會有人想要重複洗一個東西洗超過10次吧?),可以發現不同的C值會有不同的趨勢。當C=1%時,只要持續增加n就可以大幅降低殘留的比例,C=5%也是;然而當C=20%或是更高時,就會在1~3之間出現最小值。
結論:如果洗一些殘留溶液不會很大的東西,例如說磁器杯、碗,這種表面光滑的東西時,必須要分越多次洗越乾淨;而當洗一些殘留溶液較大的東西,譬如說衣物、地毯…等等會吸水的東西時,則可以考慮分較少次數洗。
從這個結論我們也可以知道,有時候清洗可樂空瓶(2L空瓶)時,我們裝了半滿的水就會懶惰的蓋起瓶蓋搖晃,然後再裝半滿水再搖晃,其實是比裝滿水以後倒掉來的有效率的做法。
故事說到這邊,或許有些眼尖的讀者可以發現一個bug!那就是,無論加入多少溶質(清潔劑、髒污),水都可以瞬間把他們全部溶解,沒有溶解的上限,也沒有溶解速率的問題。沒錯,為了讓問題比較好處理,我們假設所有的溶質是完全可溶,而且是在飽和溶解度以下的情況。但是在上面的推導中可以看到當我們分多次清洗,水的量變少時,例如說只裝20mL的水進入,或許x公克的髒東西就不能完全溶解。
另外一個問題是:上面考慮的是平衡的情況,也就是我們想像當加入足夠多的水時,溶質會立刻被水溶解,但是真實情況是,水加進去不一定會一瞬間就把溶質溶解,就好像喝咖啡加糖,一開始糖也溶不開,洗碗也會遇到這種非平衡的情況(而且我們不會等到他全部溶解,太浪費時間)。在此情況下,就會變得較為複雜而難以使用理論來研究(請看註3初步的理論),此時,就必須倚賴各位的觀察來決定清洗次數囉!
- 註1:這個方程式成立的條件為:被清洗的容器容量要大於
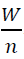 ,否則我們就無法把這麼多的水裝進容器中,而也就無法用這種方式清洗了
,否則我們就無法把這麼多的水裝進容器中,而也就無法用這種方式清洗了 - 註2: 事實上我們可以將y微分,解
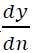 =0,並且確認找到的極值為最小值,即可”解析解”這個問題;也就是解
=0,並且確認找到的極值為最小值,即可”解析解”這個問題;也就是解 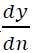 =[ln(nC)+1](nC)n=0
=[ln(nC)+1](nC)n=0 - 註3:如果沖水一次溶解溶質的量是溶質總質量以及沖水的量的函數F(x,t),也就是假如在某一次沖水前溶質的量為x,而我們沖水沖了t時間,則最後被水帶走的溶質質量為F(x,t)*C(C為L/W,與內文相同)。在這種情況下,假若剛開始髒東西為m克,每次沖水的時間T,第一次清洗後帶走的髒東西量是:C*F(m,T),殘留1-C*F(m,T),第二次為:F(1-C*F(m,T),T),殘留1-F(1-C*F(m,T),T),以此類推,為一遞迴函數。