對一般人而言,只要有錢,想要穿金戴銀就不是問題,問題是沒錢。但有機太陽能電池似乎是命格不好,即便有錢,也難以穿金戴銀:他只要用了金或銀當電極,光電轉換效率就欠佳,每每只能對著無機的同伴(矽晶太陽能電池一般以銀當電極),唱著「金包銀」的苦曲。
有機太陽能電池的命格哪裡不好?這種命格要如何改運?本館獨家結合了中國傳統易經與西洋的巴斯卡三角形理論的命理推算法可為您解答,全套八DVD售價99元,前十名call in 訂購的朋友,我們還送市價9999元的聖祖加持開運招財航太合金原子筆折價卷乙張哦!(誤)

金和銀,從古至今都是貴重金屬的代表,並做為貨幣、或是發行貨幣的擔保。這一方面是因為他們的稀有性,另一方面在於他們穩定不易變質。之所以如此,則歸功於他們有很高的功函數(work function),高功函數的物質不易被氧化。
功函數是筆者認為取名最失敗的科學名詞之一,他的定義為:「要使一粒電子立即從固體表面中逸出,所必須提供的最小能量」,這個定義與功或函數都沒有太大的關係。然而,這是了解電池運作所需知道的一個概念。
除了不易被氧化,這些貴重金屬也有較高的導電率,故成為無機(矽晶、Ⅲ-V族等)太陽能電池中廣受歡迎的電極材料。只不過一來到有機太陽能電池的世界,金、銀電極往往就不合用了。有機太陽能電池一般是以便宜的鋁當電極,鋁的功函數較低,容易被氧化,若沒有理想的封裝,太陽能電池在大氣環境下效率很快就會衰降。
為何不跟無機太陽能電池一樣選用功函數較高的金屬?是因為太陽能電池陰極和陽極間功函數的落差越大,其輸出的電壓及電流(short circuit current)的表現會越好;有機太陽能電池常選用既能透光又能導電的金屬氧化物來當做一端電極,金屬氧化物的功函數較高,傳統上做為陽極,在陰極部份只好選用功函數低的金屬囉。
若以水位比電位,則電極就像是水道最兩端的水壩。無機太陽能電池之半導體材料的p-n介面就像一個滑水道,電流如水流可以順暢地下滑,將位能轉成動能(電動勢)而衝過水壩;用於有機太陽能電池光電反應層之材料為共軛聚合物(conjugated polymer),其能階較平緩,因此需要設計些機關來導出電流。一般的常用的方法是在光反應層和電極之間再加入中介能階的緩衝層,把有機太陽能電池的水道改良成如同巴拿馬運河般多層階梯狀,電子才能逐步流出,因此電極需要選用契合各層能階的材料,亦迫使有機太陽能電池使用低功函數的金屬當陰極。
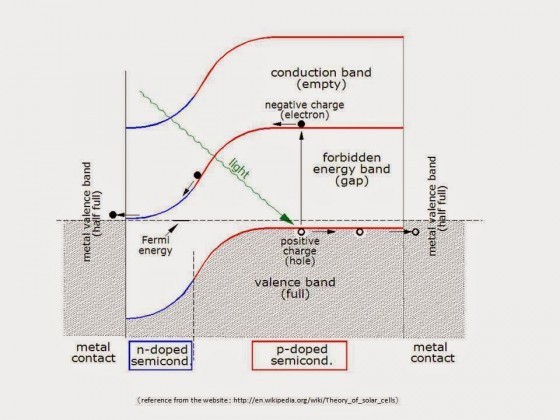
圖片來源:wikipedia
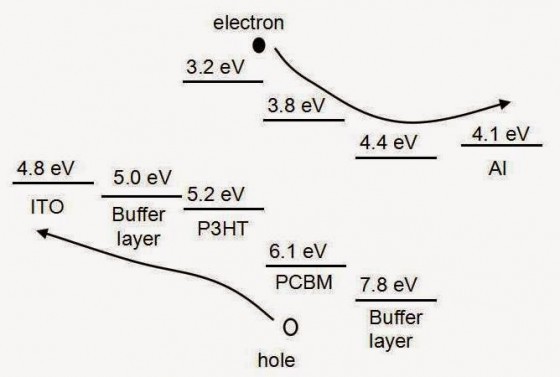
研究者們對此並不滿意,他們想直接把水壩降低,所採用的方式是在陰極與光電反應層之間再增加一層介面偶極(interfacial dipole)材料。電偶極者,正負電荷成對相依者也。正負電荷成對,之間就會有電位差,經由此電位差的調整,有機太陽能電池內的電子會把明明是高功函數的電極誤認為是低功函數,就給他這麼騎上去,嗯,我是指電流就可以順順地流過去了。
但故事並有那麼結束,一個問題的解決通常是另一個問題的開始,早期發展的介面偶極材料中(所謂的早期是2012年),有的電阻值較高,有的並沒有那容易就吸附在光電反應層上,或必需使用蒸鍍方式來成膜,如此種種提高了的製作的成本。
最近麻州大學的研究團隊合成了新的材料來當做中介層,一舉解決了上述的問題,研究成果也被發表於極具盛名的期刊「science」上。他們分別製作了以鋁(功函數低)和銅、銀、金(功函數高)來當陰極的有機太陽能電池,在沒有中介層的狀況下,高功函數陰極的樣本光電轉換效率只有2~3%,而增加了中介層後,光電轉換效率可大幅提高到8~9%。不但如此,這種合成材對光電反應層的吸附力高,可以塗佈方式成膜,這對產品是否能量產,是一個關鍵因素。
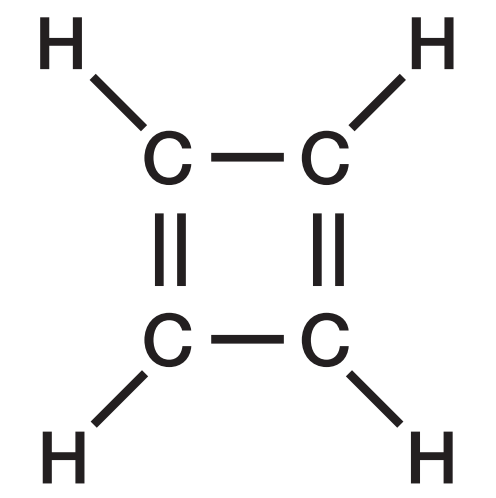
到底是什麼合成材料那麼厲害?原來研究團隊是將兩性離子(Zwitterion)接合在富勒烯(Fullerene,即C60)分子上。兩性離子,故名思義,是具有成對想依正負電荷的化合物;而富勒烯則是一種導電性佳且「親近」共軛聚合物的分子。如此可降低功函數並兼顧吸附力,雙管齊下,效果斐然!
現在只剩下一個問題了:研究團隊是如何把兩種化合物接合在一起呢?嘿嘿,這大概屬於商業機密無法外傳吧。不過各位朋友如果訂購本館結合了中國傳統易經與西洋的巴斯卡三角形理論的命理DVD,裡面或許會有答案。
註:其實從2006年開始,就有許多研究團隊把功函數高的金屬拿來當陽極,製作出被稱做「反式」的有機太陽能電池。所以說有機太陽能電池早就在穿金戴銀啦,只是以前必需倒立著穿金戴銀,現在總算可以正立了。
參考資料:
- 1. A more efficient, lightweight and low-cost organic solar cell: Researchers broke the ‘electrode barrier’.Science Daily [18/09/2014]
- 2. Zachariah A. Page et al. (2014) “Fulleropyrrolidine interlayers: Tailoring electrodes to raise organic solar cell efficiency“, Science,Vol. 346 no. 6208 pp. 441-444. DOI: 10.1126/science.1255826
本文轉載自作者部落格吳京的量子咖啡館
































 本文同時收錄於《
本文同時收錄於《