月曆28年輪迴一次？

你是否也曾在抽衛生紙的瞬間，心頭閃過「這會不會讓更多森林消失」的擔憂？當最後一張衛生紙用完，內心的愧疚感也油然而生……但先別急著責怪自己，事實上，使用木製品和紙張也能很永續！只要我們選對來源、支持永續木材，你的每一個購物決策，都能將對地球的影響降到最低。

二氧化碳是「植物的食物」：碳的循環旅程

樹木的主食是水與二氧化碳，它們從空氣中吸收二氧化碳，並利用這些碳元素形成枝葉與樹幹。最終這些樹木會被砍伐，切成木材或搗成紙漿，用於各種紙張與木製品的製造。

木製品在到達其使用年限後，無論是被燃燒還是自然分解，都會重新釋放出二氧化碳。不過在碳循環中，這些釋出的二氧化碳，來自於原本被樹木「吸收」的那些二氧化碳，因此並不會增加大氣中的碳總量。

只要我們持續種植新樹，碳循環就能不斷延續，二氧化碳在不同型態間流轉，而不會大量增加溫室氣體在大氣中的總量。因為具備循環再生的特性，讓木材成為相對環保的資源。

但，為了木製品而砍伐森林，真的沒問題嗎？當然會有問題！

砍對樹，很重要

實際上，有不少木材來自於樹木豐富的熱帶雨林。然而，熱帶雨林是無數動植物的棲息地，它們承載著地球豐富的生物多樣性。當這些森林被非法砍伐，不僅生態系統遭到破壞，還有一個嚴重的問題–黃碳，也就是那些大量儲存在落葉與土壤有機質中的碳，會因為上方森林的消失重新將碳釋放進大氣之中。這些原本是森林的土地，將從固碳變成排碳大戶。

不論是黃碳問題，還是要確保雨林珍貴的生物多樣性不被影響，經營得當的人工永續林，能將對環境的影響降到最低，是紙漿和木材的理想來源。永續林的經營者通常需要注重環境保護與生態管理，確保砍下每顆樹木後，都有新的樹木接續成長。木材反覆在同一片土地上生成，因此不用再砍伐更多的原始林。在這樣的循環經營下，我們才能不必冒著破壞原始林的風險，繼續享用木製品。

如何確保你手中的紙張來自永續林？

如果你擔心自己無意中購買了對環境不友善的商品，而不敢下手，只要認明FSC（森林管理委員會）認證與 PEFC（森林認證制度）認證標章，就能確保紙漿來源不是來自原始林。並且從森林到工廠、再到產品，流程都能被追蹤，為你把關每一張紙的生產過程合乎永續。

家樂福「從 i 開始」：環境友善購物新選擇

不僅是紙張，家樂福自有品牌的產品都已經通過了環保認證，幫助消費者在日常生活中輕鬆實踐環保。選擇 FSC 與 PEFC 標章只是第一步，你還可以在購物時認明家樂福的「從 i 開始」價格牌，這代表商品在生產過程中已經符合多項國際認證永續發展標準。

「從 i 開始」涵蓋十大環保行動，從營養飲食、無添加物、有機產品，到生態農業、動物福利、永續漁業、減少塑料與森林保育，讓你每一項購物選擇都能與環境保護密切相關。無論是買菜、買肉，還是日常生活用品，都能透過簡單的選擇，為地球盡一份力。

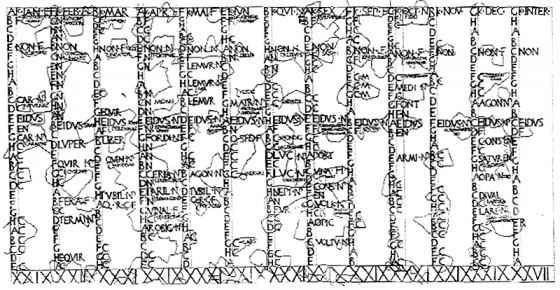
四年一度的 2 月 29 日又來臨了，你是否有想過，到底是誰發明了這個莫名其妙多出來的一天呢？其實，我們現在使用的西曆，是源自於古羅馬的曆法，其中變遷的故事還真是源遠流長。

為什麼是加在 2 月 29 日而不是 12 月 32 日？

我們先來想想看，「 2 月 29 日」這個玩意兒，有什麼地方不太尋常的？先來問你一個問題：照常理來說，應該把多餘的日子加在一年的最後面才對，那不就應該是「 12 月 32 日」了，人們怎麼會選擇創造一個「2月29日」呢？

你可能會說，這個問題還需要想嗎？因為 2 月日數最少啊！2 月只有 28 天，加上個 29 日聽起來不怎麼奇怪；12 月已經有 31 天了，再加上一個 32 日也太好笑了吧！不過，事情沒有這麼簡單。

在早期的羅馬曆法（羅慕路斯曆）當中，其實一年只有十個月。這件事情在現在各月份的英文名稱當中，還留下了明顯的痕跡。例如說，十月的英文是 October，但是 octo -開頭的字是代表「八」的意思，所以 October 顧名思義是「八月」的意思！可以去看，章魚（octopus）是八隻腳的生物，而八邊形的英文稱為 octagon。那問題來了，為什麼「八月」突然變為十月了呢？

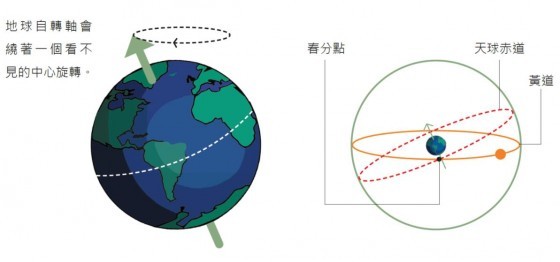
事情發生在羅馬國王努瑪‧龐皮留斯（Numa Pompilius）的時候，當時發現原本每年十個月、304 天的曆法，造成每年年初的季節都不同了，人們的生業週期與曆法格格不入。這個道理很簡單，地球繞太陽公轉一圈（當然那時候人們不清楚地繞日這回事）大約 365 天，稱為一個「回歸年」，也就是太陽在黃道的位置移動了 360 度的時間。太陽「回歸」了之後，代表季節週期也「回歸」了一次，人們生產的週期也就又「回歸」了一次。

一年 304 天的古曆，實在與回歸年差距太大了，所以努瑪決定加上兩個月，讓曆法的一年變為 355 天，較接近太陽的週期。不過這時候，Ianuarius（January）和 Februarius（February）是加在一年的最後面，而不是一開始。

這個 355 天的曆法，我們就可以看出一些天文意義了。

第一，如我們剛才說的，比起原先的曆法，已經較為接近一個「回歸年」，符合地球上人們真實感受到的季節遞嬗週期。第二，這個數字不是沒有來頭的，它符合月亮盈虧的週期。月亮繞著地球公轉的週期有好幾種算法，其中一種稱為「朔望月」，也就是盈虧的週期，大約 29.53 天。計算一下，12 個朔望月大約 354.4 天，因此把曆法一年訂作 355 天是具有天文意義的。

不過，接下來還有個問題，355 天還是不到 365 天，要怎麼補足呢？方法就是閏月了。那時候，人們的作法是一年的最後一個月：Februarius（February）身上動手腳，他們把這個月縮減到 23 或 24 天，接著在後面加上一個 27 天的閏月。掐指一算，這個「二月」原本有 28 天，被減去了 4 到 5 天，但後面的閏月加上了 27 天，所以置閏的年就有 377 或 378 天了。後來置閏的方法改了好幾次，Februarius（February）也從一年的最後一個月變為第二個月，但手腳仍然是動在 Februarius（February）身上，到現在依然如此，所以閏年的時候多出來的才是 2 月 29 日，而不是 12 月 32 日了！

一年有兩個 2 月 24 日

在努瑪之後，羅馬另一次重大的曆法變革發生在西元前 46 年，主角是眾所周知的尤利烏斯‧凱撒（Julius Caesar）。凱撒打贏高盧戰爭與內戰之後，集大權於一身，並改革曆法，此新曆稱為「儒略曆」（Julian calendar）。為了整頓曆法，他先將西元前 46 年擴充到 445 天，隔年開始則按照他的規律。

凱撒的曆法，試圖解決一個問題：回歸年並不是正好 365 天，而是 365 天又 6 小時左右。他的做法是單一的「閏日」，置閏的位置是在「三月的第一天（Kalends of March）數回去第 6 天」，也就是 2 月 24 日。閏年稱為 bissextile （”twice sixth”，意思是「兩個第六天」）。那時候沒有所謂的「 2 月 29 日」，而是把 2 月 24 日延長為兩天的時間，但在法律上那兩天算作同一天，也就相當於有一個長達 48 小時的日子。

只不過，人算不如天算，新曆法實施沒多久，一件驚天動地的事情發生了──西元前 44 年，凱撒被暗殺了！原本凱撒的要求是每四年置閏一次，但此後死無對證，發生一個嚴重的誤解，人們三年就置閏一次。這樣一來，西元前一世紀的閏年發生好幾次錯誤，直到數十年後羅馬帝國君主屋大維（奧古斯都）才減少了幾次閏年，來彌補多閏的那幾次。一般認為，彌補之後恢復正常曆法的時間是西元 8 年。

每四年有一次 29 天的二月，理論上是在凱撒啟用儒略曆時開始，但因為陰錯陽差，其實過了五十年左右，到了奧古斯都的時候才正式上軌道。當初的作法是延長 2 月 24 日，到了這幾百年才變成外加一個「 2 月 29 日」的方式。

消失的十天：格列哥里改曆

剛才我們對於「回歸年」的估算，還不夠仔細。依據現代的測量，我們知道，一個回歸年實際上是 365.2422 天。儒略曆每四年閏一次，所以它的一年平均是 365.25 天，乍看之下和回歸年差不多，但過了幾百年後就開始有差別了！簡單估算，一年差了約 0.0078 天，從西元元年到西元 1500 年，就可以差了 10 天左右了！

每年差一點點，對於人們生活週期可能還沒有太大的影響，但是對於宗教節慶就有不可輕忽的改變了。由於復活節的時間，是從春分的時間推算而來的。曆法上的年，與太陽、地球真實關係的回歸年有所偏移，就代表每年春分的時間位在曆法上的日期，也不斷地偏移。春分的時間偏移，復活節的時間也就跟著偏移，這對教廷來說是件大事。

於是，在 1582 年，教皇格列哥里十三世宣布改曆。他做了兩件事情：第一件事，改變置閏的規則。為了讓每年春分時間一致，必須讓曆法的年逼近回歸年。原來年份只要是 4 的倍數就要置閏，但這樣閏太多了，使得曆法平均一年（365.25 天）超過回歸年（365.2422天）太多，因此需要砍掉幾個閏年來修正這個餘額。這時採取的辦法是這樣的：以後年份如果是 100 的倍數但不是 400 的倍數，就不是閏年了。也就是說，西元 1700、1800、1900 年都不再是閏年，但 2000 年仍然是閏年。

以上的作法，將「 4 年 1 閏」變為「400 年 97 閏」。簡單計算一下，1/4=0.25，儒略曆平均一年 365.25 天；97/400=0.2425，格列哥里曆平均一年 365.2425 天，與回歸年的誤差縮減到每年 0.0003 天，到三千多年左右才會誤差一天。這套格列哥里曆，就一直沿用成為現代的「公曆」了。

格列哥里改曆，還做了第二件事情，目的是要讓春分回到 3 月 21 日，才能維繫復活節原定的時間。因此，他做了一個立即的修正，等於是大刀砍下去，把之前偏差掉的全部改了回來。還記得嗎？我們剛才估算的結果，儒略曆經過一千多年，整整多出了 10 天左右。這時候，教皇格列哥里十三世作法很直接，直接在 1582 年砍掉 10 天！所以，1582 年 10 月 5 日到 14 日，這十天就因為這次改曆而消失了。

然而，不是全世界都立刻採用這套曆法，並配合「消失的十天」。早在西元 1054 年，羅馬公教與東正教早已大分裂，這時羅馬教皇宣布改曆，東正教也就經過很多年都不認帳了。歐洲最後一個採用格列哥里曆的國家是希臘，採用的時間已經到 1923 年了。

那現在還有人在用古老的儒略曆嗎？廣義地說，其實還是有的，這種人叫作「天文學家」。你會覺得很奇怪，曆法不就是因為天文學家對太陽、地球運動的更嚴密計算，講求精確才不斷改正嗎？那為什麼天文學家自己偏偏要使用舊的標準呢？

是這樣的，「閏年」的修正，是為了讓以「年」為週期的曆法，配合真實自然界的季節變化、太陽位置。一般人的生活、宗教儀式都需要以「年」為週期，但是天文學的紀錄沒有這個必要。「年/月/日」這樣的紀錄，在許多運算上太過麻煩，天文學家為了方便，只要一套以「日」為單位的系統，不斷遞加上去就好了。嚴格來說，天文學家用的也不是「儒略曆」了，而是一套以儒略曆定義的起點為標準的「儒略日」。比如說，今天是 2016 年 2 月 29 日，但儒略日記作「2457448」，後面還可以加小數點。網路上很容易找到公曆轉為儒略日的換算工具，可以上去試試看！

2016 年多出了一個 2 月 29 日，別以為是天上掉下來的禮物囉！人們對於天體運行規律的了解越來越多，又由於宗教等因素，才漸漸使得曆法中的一年接近自然界的「回歸年」。不管是有 48 小時的 2 月 24 日，還是多出一個 2 月 29 日，地球才不管這些呢！地球依然按照它的規律繞著太陽公轉，人們則配合自然規律來調整自己的生活步調。時間不斷在往前進，乍看之下多出了一天，其實地球的工作從不罷休喔！

參考資料：

• Bonnie Blackburn and Leofranc Holford-Strevens, The Oxford companion to the year (Oxford: Oxford University Press, 1999).

吳昌任／臺北市立南湖高中地球科學教師。
林詩怡／臺北市立中崙高中地球科學教師。
兩人合著有《追星族的天空奇緣》（第49 梯次好書大家讀推介）、《星空球》（2013 年好書大家讀知識性讀物組）

人生總會有不那麼順遂的時候，明明已經盡力了，事情還是不如所願，唯有當事者得到一個合理的解釋，心情才得以釋懷，最常見的就是把這些無法解釋的遭遇歸咎於運勢。

占星術到底是真是假？從它的定義可以略知一二。鮮少有不合邏輯的騙術能存在許久，所以如果想要知道如何利用天文現象創造出占星術，就必須先把天文學研究清楚。早期研究天文是為了種族的延續，例如從日、月的運行訂出曆法，讓人民可以在規律的季節變化中，知道何時該做哪些事，使得糧食無缺同時避免災害。掌握天體運行的韻律之後，曆法主要架構就完成了，接下來只剩下微調，讓曆法可以長時間與日月運行吻合，這時候就有多餘的時間可以想想天上世界與地上人間的關係。

現在大家所說的占星術是沿自於巴比倫時代，也就是說，如果你想要瞭解占星術是真是假，就要先知道巴比倫人是如何定義各種影響運勢的星座。現在我們就先從最簡單的開始解說起。

每個人都可以從出生日期對照出自己的星座，這就是跟運勢有關的星座，稱為太陽星座。經過長時間的觀察，巴比倫人發現一年之中太陽會在恆星之間移動一整圈，這個軌跡稱為「黃道」，而這些經過的星座就稱為「黃道星座」。巴比倫人認為，當太陽位於哪個星座裡就主宰了人的個性。不同星座的人的個性為何，則是來自於人類對於這個星座的想像與解釋。以天蠍座為例，天上一部分的星星連起來像是蠍子的形體，所以稱為天蠍座。蠍子不會隨時用毒針攻擊，但是當要保護自己時，就會用毒針刺對方。所以天蠍座的人一下子表現出愛，一下子又讓人很受傷，簡單的說就是又愛又恨。

如果世界上真的只有依照太陽星座去區分的12 種人，民眾不會想要相信占星術，因為你很容易就可以找到和你是同樣的太陽星座，但是個性與成就卻不同的例子。天上的星體不是只有太陽會相對於星星移動，所以太陽星座的定義可以用在從地球上看起來會相對於星星移動的其他天體上，例如：月球與行星，這讓占星術有更高的說服力。

一個月當中，月球與太陽的相對位置會改變，造成不同的月相，所以同一個太陽星座的人，其月亮星座可能會不一樣。太陽星座與月亮星座都相同的人，其金星星座、水星星座、火星星座、木星星座與土星星座的其中一些可能不一樣，如此一來，就可以把人分成12 的7 次方，也就是3 千5 百多萬種！這麼多的組合可能，對於當時的人口來說已經綽綽有餘，所以巴比倫人相信占星術能解釋每個人的差異，也不足為奇。

你可以想出挑戰占星術的其他例子嗎？說說雙胞胎吧！早期沒有超音波科技，四十幾年前的孕婦懷了雙胞胎也不知道，直到生產當天發現生了一個小孩之後肚子沒消下去，才知道還有一個小孩在肚子裡，所以當時的雙胞胎出生時間可以相差一個小時左右！

雙胞胎的太陽、月亮以及行星星座都相同，但是個性卻不一定相同。為了要解釋這個現象，占星術又增加了一小時以內就會出現變化的上升星座與下降星座。顧名思義，出生瞬間會有一個黃道星座一部分在東方地平線上，一部分在東方地平線下，這個黃道星座就稱為上升星座，同時在西方地平線附近的則是下降星座。因為地球自轉的關係，星星大約是以一小時15 度的速度持續繞著天球北極旋轉，所以如果你想要以雙胞胎的例子來挑戰占星術，就會因為出生的時間差，使得上升星座與下降星座在地平線上的比例不同，占星術就這樣把人又多分了144 倍的種類，數量約51 億，同時也解釋了雙胞胎個性不同的問題。

當心靈很脆弱的時候，即使是很平常的描述，你都會覺得說得很準，此時越是要小心有心人士利用這個時候讓你對他掏心掏肺的。我們再來討論一些從巴比倫時代到現在的天文事實，看看這些是如何影響占星術的。

你的生日當天，太陽真的還是在巴比倫人觀察到的那個位置嗎？

根據定義，出生當天從地球上看起來，太陽應該是在你認為的太陽星座的方向上。但是地球自轉軸的方向並不是固定的，比較像穩定旋轉之後的陀螺一樣，旋轉軸會慢慢的繞著一個看不到的中心旋轉，這樣旋轉一圈要大約兩萬六千年。垂直於地球自轉軸的赤道向外延伸到星空中，就稱為天球赤道，而天球赤道與黃道的其中一個交點被訂為一年的開始，在經過長時間的曆法變革之後，太陽運行到這個交點就是該年的3 月21 日，這個點稱為春分點。

當地球自轉軸改變指向的時候，天球赤道會跟著改變方向，使得春分點的位置移動，中國把這個現象稱為歲差，也就是說，一樣是3 月21 日，巴比倫時代看到太陽在天上的位置與現在觀察到的位置已經不同了。如果你在生日當天觀察太陽在天上的位置，可能已經不在你認為的太陽星座方向了。此時根據定義來看太陽星座的出生日期範圍，結果會與你之前認為的很不一樣，相差了三個星期左右。舉例來說：1 月28 日出生的人，根據以前的定義是水瓶座，但是現在1 月28 日太陽是在魔羯座的範圍裡。

為什麼以前只有12 個黃道星座，現在卻有13 個？

這是最近幾年又將占星術炒熱的話題之一，也讓占星術又重回大家聊天的話題中。會出現第13 個星座，代表一年當中的某段時間裡，黃道會經過第13 個星座：蛇夫座的範圍。究竟是黃道的位置改變了？還是巴比倫人沒有發現這一件事？

四千多年來，黃道的位置變了嗎？

如果地球繞太陽的軌道面改變了，那麼黃道的位置就會變。根據長久以來的觀測紀錄看來，地球繞太陽的軌道面並沒有什麼變化，也就是說，黃道並沒有在這四千多年內改變位置，所以黃道第13 星座並不是因為這樣才出現。

巴比倫人沒有發現黃道經過蛇夫座嗎？

左下的圖為人馬座、天蠍座與蛇夫座附近的星空，為了標示清楚，加上了星座連線，你很清楚的看出這三個星座以及黃道的位置，你覺得黃道有經過蛇夫座嗎？是不是就很明顯的看出來，在某一些日子裡黃道真的經過蛇夫座的一小部分，而這延伸出這個部分的星星不是很亮。

由影像就可以看出來，巴比倫人不是故意忽略掉蛇夫座，而是在沒有訂定出星座界線以前，這一段目前認為經過蛇夫座的黃道，會被認為是在天蠍座裡的。也就是說，會出現第13 個黃道星座，其實是訂出星座界線之後的結果，而星座界線是國際天文聯合會（IAU）為了將天上的星星清楚界定是隸屬於哪個星座，避免同一顆星有不同的名稱所制訂出來的。因為星座界線的出現，才會有黃道第13 星座的誕生。

占星學家發現了這個事實以後，就必須創造出蛇夫座的個性。記得嗎？方法就是依照星座的形象加以擴張。蛇夫座的人喜歡控制別人，因為蛇夫座就是一個抓住巨蛇的人，這樣你就更能了解星座個性是怎麼來的了吧！

每個星座的生日日期範圍都是一個月左右嗎？

有了星座界線，我們就可以更準確的依照定義把哪幾天出生的人屬於哪個星座重新判斷一次。如果你有可以標示出日期與太陽位置的星空球，就可以發現太陽在每個黃道星座範圍裡的日子並不一樣長，在室女座的範圍內可以長達四十幾天，而在天蠍座裡卻不到十天。

巴比倫人知道天王星、海王星、冥王星嗎？

八大行星裡的金木水火土，是人類用眼睛就可以看到的5 顆行星，所以古文明皆有這5 顆行星的紀錄，其他的三顆行星因為距離地球較遠，都是透過望遠鏡才發現的。巴比倫人不知道天王星、海王星、冥王星的存在，怎麼可能會把這3 顆行星的影響放入星座運勢裡呢？可想而知，現在你看到運勢裡面提到天王星、海王星、冥王星的部分，都是這幾百年來的占星學家加進去的。

冥王星後來被改列為矮行星，它對於星座運勢的影響還有這麼大嗎？

冥王星被發現後沒多久，天文學家就知道它的質量、體積很小，但當時的占星學家為了趕上最新的科學進展，紛紛把冥王星的影響加入星座運勢中。結果2009 年冥王星被國際天文聯合會改列為矮行星，這些曾經說冥王星影響了運勢的人現在是不是該改回來？如果冥王星還是擁有這麼大的影響力，那麼和它一樣都屬於矮行星的穀神星（Ceres）、女戰神（Xena）等，是不是也該納入影響運勢的因素之中？

知道今日的占星術有這麼多矛盾之處之後，大家應該回到占星術當時發展出來的時空背景，正確的瞭解它的用意。但是，我們也不需要把占星術當作是萬惡，只要不迷信就好了。反之，我們可以用占星術來提醒自己往更好的方向前進。如果你覺得星座運勢當中好的部分和你對自己的期待還滿像的，何不把這些描述記在心理，讓自己朝著這個方面前進。至於那些不好的描述，就不要太在意了！

〈本文選自《科學月刊》2016年1月號〉

延伸閱讀：
銀河導航系統
探索最美麗浩瀚的研究領域—中研院天文所所長賀曾樸專訪

什麼？！你還不知道《科學月刊》，我們47歲囉！

入不惑之年還是可以當個科青