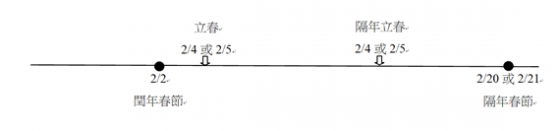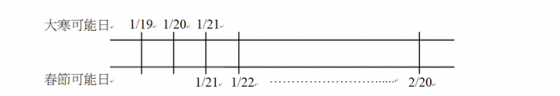「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類金獎 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:李尚謙/臺中市立文華高級中學
立春是二十四節氣中的第一個節氣。古人常藉詩詠懷,如唐代詩人白居易曾寫道:「立春後五日,春態紛婀娜。白日斜漸長,碧雲低欲墮。」描寫的便是立春過後,春意漸濃的各種景物。

今年除夕在某網路媒體(2019.02.04)出現與立春相關的報導——
「標題:《超罕見》今天除夕逢立春、豬年『兩頭無春』!下一次要等到2057年
內文:今年農曆除夕巧遇二十四節氣中的『立春』,也因此即將到來的農曆豬年『兩頭無春』。這種情況非常非常少見,100年裡只有3次,分別是2019年2月4日、2057年2月3日、2076年2月4日。換句話說,過了今天,下一次得等到38年之後的2057年……
另外值得一提的是,農曆豬年為2019年2月5日至2020年1月24日,2019年的立春在2月4日,此時仍然是農曆狗年,2020年的立春同樣也在2月4日,但那時已經是農曆鼠年了。所以農曆豬年沒有『立春日」,也就是所謂的『兩頭無春』。
中國民間有一種說法,『兩頭無春」的年份在是『寡年』『盲年』,不適合嫁娶。」
這篇報導提到了一個說法——「兩頭無春」,並強調 100 年中只出現了 3 次。這引起了我的好奇,究竟什麼是「兩頭無春」?真的如此少見嗎?會不會有其它的可能性呢?
首先我搜尋了農曆與 24 節氣的規則,農曆其實是陰陽合曆,既考慮太陽運行的迴歸年,也納入月球運行的朔望月,朔望月平均長度 29.53 天,以朔日(完全没有月亮的那一天)為每月的初一日,農曆没有閏月的年份(以下簡稱農曆平年)有 12 個月,只有 354 或 355 天。有閏月的年份(以下簡稱農曆閏年)有 13 個月,總天數為 383 或 384 天。因此在農曆平年天數比國曆少了 11 天左右,但農曆閏年比國曆多了 18 天左右。而相鄰兩節氣間隔天數約 15 或 16 日,同一節氣例如春分至下一個春分的間隔是固定的,約是一個迴歸年的日數 365 或 366 日。
因農曆平年比迴歸年少了 11 天,小於相鄰兩節氣間隔天數,有可能少了某一個節氣,所以平年節氣數為 23 或 24 個。而農曆閏年比迴歸年多出 18 天,大於相鄰兩節氣間隔天數,必會多出一至二個節氣,所以閏年節氣數為 25 或 26 個。
接著我想要知道農曆閏年多出或平年短少的節氣一定是立春嗎?
我查詢了農曆置閏的規則,其中最重要的是若兩個相鄰的冬至間(即歳實)有 13 個朔日(就是没有月亮的日子即初一),則此歳中第一個無中氣月需設置閏月。另一個相關的規則是冬至必在農曆十一月內,而冬至通常在國曆 12/21 或 12/22。若冬至落在最早的農曆十一月初一,則正月初一就出現在二個月後。若冬至落在最晚的農曆十一月三十,則正月初一就出現在一個月後。因此春節通常出現在國曆 1/21 至 2/20 間。
按此推算,因農曆閏年較迴歸年多出約 18 至 19 日,而翌年的春節不可能晚於國曆 2/20,所以農曆閏年的正月初一不可能晚於國曆 2/2,自時憲曆 1645 年施行一千年內,閏年春節出現在最晚的 2/2 有三次,分別是 1832 年、2204 年、2318 年。
若閏年春節出現在最早的國暦 1/21,翌年的春節將出現在 2/8 或 2/9。
若閏年春節出現在最晚的 2/2,翌年的春節將出現在 2/20 或 2/21。
因此,無論閏年春節出現早或晚,該年都將有兩個立春。而平年天數較迴歸年少,節氣數只會少於或等於 24 個,不會有第二個重覆的節氣,故雙立春必僅出現在閏年。
接下來我想知道除了立春以外,有没有其它節氣會有類似的狀況嗎?
上文提到春節通常在國曆 1/21至2/20 間,這段時間可能經歷 3 個節氣,依序為大寒(1/19~21)、立春(2/3~5)、雨水(2/18~20),若春節早於大寒或立春,或者晚於雨水,在一個農曆年內就有可能頭尾重覆出現同樣的節氣,立春已於上文討論,只剩下大寒與雨水有機會。
所以農曆年有可能包含兩個雨水嗎?
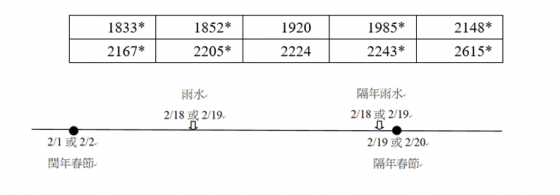
雙雨水的出現,除了必要的閏年條件外,因閏年的春節最晚出現在 2/2,必在雨水(2/18~20)之前,所以若下一年的春節晚於雨水出現的日子,農曆閏年即可包含兩個雨水。
(1)若雨水在國曆 2/18,那麼春節應該出現在 2/19 或 2/20。
(2)若雨水在國曆 2/19,那麼春節應該出現在 2/20。
(3)若雨水在國曆 2/20,除非春節出現在正常區間以外的 2/21。
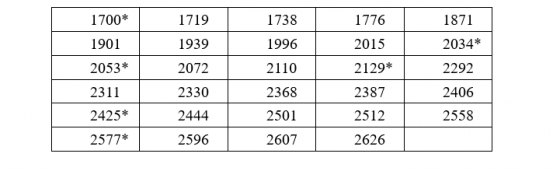
在 1645 年到 2644 年的 1000 年當中,春節次數統計如下表
出現在國曆 2/19 的 29 次春節中,其中有 6 次(*)雨水出現在 2/18。下圖以西元年依序排列
出現在國曆 2/20 的 10 次春節中,其中有 8 次(*)雨水出現在 2/18 或 2/19。
以過去最接近的 1985 年為例,春節出現在 2/20,當年的雨水出現在 2/19,那一天是農曆甲子年的 12 月 30 日,前一年 1984 年的雨水也在 2/19,那一天是農曆 1 月 18 日,也就是 1984 甲子年出現了兩個雨水。雙立春雙雨水常被視為吉兆,象徵風調雨順、國泰民安,下一個將到來的雙春雙雨將出現在 2033 癸丑年。
更極端的例子出現在 2319 年,在 1000 年中出現了唯一 2/21 的春節,當年的雨水在 2/20,那一天是農曆戊戌年的 12 月 30 日,前一年 2318 年的雨水在 2/19,那一天是農曆戊戌年的 1 月 18 日,也就是 2318 戊戌年出現了兩個雨水。
總結在 1000 年中,雙春雙雨共出現了 15 次,但頻率並不固定,相鄰兩次間隔可近至 19 年,但也可超過 150 年,依西元年表列如下:
那麼農曆年有可能包含兩個大寒嗎?
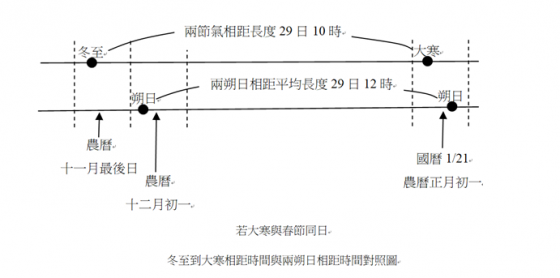
農曆年若要包含兩個大寒,除了必要的閏年條件外,春節必須出現的極端地早,必須早於或至少等於大寒日,而大寒通常在國曆 1/19 至 1/21,春節通常在國曆 1/21 至 2/20 間,如下圖如示。春節早於大寒日的可能性極低,但有機會出現在 1/21 最晚的大寒日,亦即大寒和春節同時出現在 1/21,
若大寒和春節同時出現在 1/21,連帶地排在前二個序位節氣的冬至也會最晚,應該出現在可能日期中的農曆十一月最後一日。冬至到大寒為相鄰兩中氣,差距約 29 日又 10 時,變動不大,而十二月初一到正月初一為相鄰兩朔日,差距為一個朔望月,變動幅度較大,最長可達 29 天 19 小時,最短為 29 天 6 小時,平均長度約為 29 天 12 小時。冬至與農曆十二月初一相差一日,但兩節氣相距時間與兩朔日相距時間相差有限,幾乎相等。
下圖假設大寒與春節同為 1/21 的情況真的發生時,冬至和朔日間的關係,可以看出大寒與春節同時出現在國曆 1/21 的可能性非常低,幾乎不可能發生。
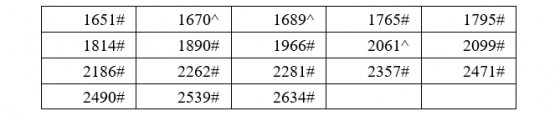
在1645年到2644年的1000年當中,1/21春節只出現了18次。依西元年排列:
其中没有任何一次大寒出現在 1/21,這意味著自 1645 年時憲曆施行後一千年內並未出現雙大寒的情形。
我將以上資料與推論作一個總整理:
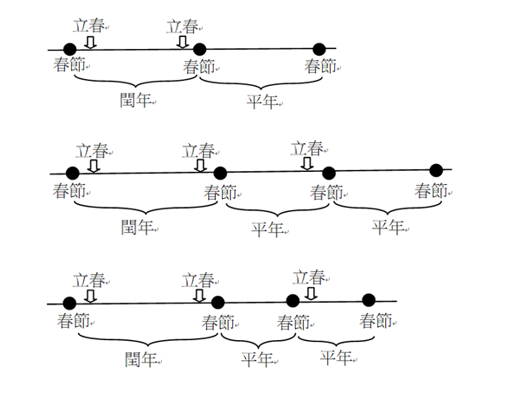
(一)農曆閏年是雙節氣的必要條件,閏年必有雙立春,雙立春必出現在閏年,約二至三年出現一次,出現雙春的下一年未必無春。若 2 年一閏,第一年閏年必有雙春,第二年平年必無春,若 3 年一閏,第一年閏年必有雙春,第二年平年可能為尾春或無春,對應第三年平年可能為無春或頭春,如右圖。
在農曆 19 年 7 閏周期中,必有 19 個立春。7 個閏年代表有 7 個雙春年,每一個雙春年必對應一個無春年,剩下 5 個單春年,但單春年的立春出現在年頭或年尾皆有可能。
雙春年出現機率為 7÷19≒0.37,無春年出現機率也為 7÷19≒0.37,反而一年內只有一個立春的單春年出現機率只有 5÷19≒0.26,平均約 4 年才會出現一次單春年。
(二)除了雙立春以外,農曆閏年也可能出現雙雨水,但難得一見,在 1645 年到 2644 年的 1000 年當中,雙立春雙雨水共出現了 15 次,間隔並不固定,出現機率為 15÷1000=0.015。
(三)出現雙大寒的可能性極低,1000 年中未曾出現過。
(四)除了立春與雨水外,同一個農曆年內不會有其它節氣重覆出現。
媒體報導中的「兩頭無春」非常非常少見,100 年裡只有 3 次,應是指除夕適逢立春,翌年又是無春年的特殊情形,即便如此,仍比不上雙雨水的百年罕見。
面對誇大的新聞標題,我們應保持理性客觀檢視並深入探討,才有機會撥雲見日。
參考資料
- 維基百科-農曆
- 風傳媒:超罕見》今天除夕逢立春、豬年「兩頭無春」!下一次要等到2057年
- 新加坡國立大學數學系:The Mathematics of the Chinese Calendar
- 新唐人電視台:東風化雨逐西風 又是一年立春時