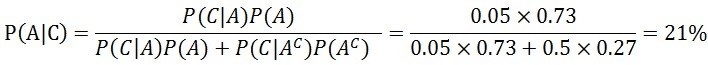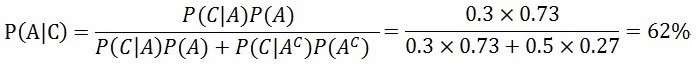對於渴望戀情的單身男女來說,「看人」是非常重要的技能。更精確地說,「適婚年齡+單身+其實不想單身」的人,某種程度上正是缺乏了看人的能力才會單身。

看人很困難。曖昧中的男女總在內心扮演福爾摩斯,觀察細節,然後開玩笑、但也帶著幾分認真的加分扣分。
約會遲到10分鐘扣5分;聊天聊到一半回LINE訊息扣9分;隔桌小屁孩哭哭啼啼比飛機降落還吵,她只哄了兩分鐘,小孩就變得比孫芸芸代言的高級家電還安靜,加10分;聽到我不好笑的笑話還笑,加20分(但這樣代表品味不是很好,就事論事依然得扣1分)。
笑容很可愛加30分。
我們用簡單的加減法評量對方。只是,這種加分扣分真的正確嗎?
或許,比起算總分,我們應該翻轉思維,思考眼前這人有多少機率,會是我的理想情人。然後,再利用托馬斯·貝葉斯所發明的機率定律——貝氏定理,來計算機率。
※
貝氏定理告訴我們,每位對象都有一定的機率是理想情人。約會的每個當下,我們都能算出這組「理想情人機率」。倘若發生了新事件,再利用新事件來更新機率值。
請想像這樣的小劇場,女主角是剛學會貝氏定理的芷帆:
※
某天上午,朋友傳LINE訊息問起芷帆的感情狀態,她清楚這是開場白,對方昨天才按讚了自己的臉書大頭貼照,照片裡只有一杯黑咖啡,旁邊擱了幾顆糖,就像她一樣,獨自裝滿了苦、澀、酸,唯獨與甜絕緣。

「我男友的好朋友剛好也單身。」
剛好是怎樣,單身一點都不好啊。芷帆心裡嘀咕。不等芷帆回答,朋友彷彿業務介紹商品般滔滔不絕描述,身高175公分,BMI低於20,在101大樓上班,興趣是閱讀,特別是科普類書籍。遮住嘴巴像王力宏,遮住眼睛像謝霆鋒,整張臉遮住像金城武。
「為什麼遮住臉像金城武?」芷帆忍不住問
「手指像。」
朋友傳了照片。雖然不到她描述的那麼誇張,但外表是芷帆喜歡的類型,手指很修長,真的有點像金城武有的手。依據過去約會、認識異性的經驗,芷帆內心進行了一段超級電腦也無法模擬的運算,吐出一個她也不知道怎麼來的數值:
這男的,有35%的機率是我的理想情人。
我們稱這個為先驗機率(a priori probability)。
※
做為理想情人的機率超過三成,芷帆決定給男孩一個機會,他叫思綸。
交換聯絡方式後,思綸約芷帆周末在台北中山站的咖啡廳見面。那是一間浪漫的白色系咖啡廳,挑高天花板,頂樓有一整面落地窗,還有一整排的白色書架、上面放了日式雜誌以及剪修整齊的盆栽。芷帆早到十分鐘,一走上樓,發現思綸已經坐在靠窗的座位上了。
看見芷帆,思綸起身過來。
「靠窗的風景很漂亮,我就想早一點到,來等這個座位。」
芷帆清楚,這間咖啡廳沒辦法預約座位,想搶到窗邊特等席,最少得提早來半小時。她看見桌上剩一半的水瓶,還有思綸真誠的笑容,心想,他可能是一位很誠懇的好男孩,努力想讓第一次約會變得完美。
但也可能是一位千錘百鍊的情場浪子,每一個步驟都經過精心設計。
芷帆想起前陣子學到的貝氏定理,她決定透過貝氏定理,仔細檢驗眼前的這位男生。貝氏定理問,
如果是適合芷帆的好男孩,特地早到的機率是多少?
如果是不適合芷帆的浪子,特地早到的機率是多少
我們用A和B各自表示「芷帆的理想情人」和「特地早到占位子」這兩個事件。方才貝氏定理的這兩組提問,可以用條件機率來表示。
適合芷帆的好男孩,特地早到的機率=P(B|A)。P(B|A)的意思是,給定A事件發生的情況下,B事件發生的條件機率。
不適合芷帆的浪子,特地早到的機率=P(B|Ac)。Ac表示與A事件剛好相反的事件。
※
根據過往經驗,芷帆認為好男孩早到的機率很高,P(B|A)=90%。壞男孩早到的機率低一點,一方面他們得和很多人約會;另一方面,他們通常擅於言詞,早到獨自坐在那裏,不能發揮他們的強項,因此機率P(B|Ac)只有70%。
出門前的先驗機率「思綸有35%的機率很適合她」,寫成數學式子為P(A)=35%,P(Ac)=65%。現在要做的,是將先驗機率和剛才的兩組條件機率整合。
「不好意思,我去一下洗手間。」
芷帆躲進廁所,在紙巾上寫下貝氏定理的公式
公式的左邊P(A|B)是所謂的事後機率(a posteriori probability)。意思是當發生B事件(特地早到)後,我們得到了新的觀察,因此事件A(思綸是芷帆的理想情人)的機率將隨之改變。
發生的事件越多,得到越多的觀察,就越了解對方,能得到更精確的機率估測。
這就是貝氏定理的精神。
芷帆按起手機計算機
計算結果表示,發生B事件後,「思綸是適合她的好老公」的機率從35%提升6個百分點,來到41%。這組機率值,將成為下一次新事件的先驗機率。
事情往好的方向前進了。鏡子裡的芷帆露出笑容。

※
一年後,場景來到飯店的婚禮套房。晚上十點,芷帆跟思綸送客的禮服都還沒換,兩個人癱在床上。
「原來辦婚禮這麼累。」
「有經驗後,下次就輕鬆多了。」
芷帆白了他一眼,思綸故作害怕地拿領帶遮住眼睛。安靜了一會兒,思綸說
「我覺得阿,婚禮會弄得這麼忙,搞不好是老祖宗的智慧。」
「為什麼?」
「要是不累,我應該一整天都會瘋瘋癲癲,過度亢奮。」
思綸轉過來看著芷帆
「娶到妳,是我這輩子最開心的一件事。」
芷帆沒接話,雙頰泛紅。這人總是這樣,像突襲檢查的方式說浪漫話。她想起這一年來,他們相處的點點滴滴,每一次事件,芷帆都細心地用貝氏定理檢驗,達到真正的「加機率值」、「減機率值」。
當思綸求婚時,他是理想情人的機率已經超過90%,芷帆眼眶泛淚,開心地答應。
「半年前,妳想分手的時候,我以為一切都要完了。」
思綸又是突然的一句話,勾起芷帆一段回憶。
※
半年前的某晚,他們約好見面。到了餐廳,芷帆卻連絡不上思綸。手機沒開、LINE訊息不回,連已讀的勾勾都沒有。
「嗯?妳不是傍晚來我們公司,思綸出去見妳,回來就早退……」
說到一半,同事才意識到不對勁,但已經來不及替思綸隱瞞了。芷帆跑去思綸公寓樓下等,直到半夜,才看到思綸的車從巷口駛進來。
「她論及婚嫁的男朋友劈腿,被發現後不但沒道歉,那男的還決定跟第三者在一起……妳聽我解釋,我手機剛好沒電,她情緒又很不穩定,我決定先安慰她,晚上再跟妳解釋。」
她是思綸的前女友。
他們是學生時代的情侶,交往過五六年,相處起來像家人。雖然分手多年,但芷帆總認為,如果思綸會離開她,一定是因為那女的緣故。也因為這樣,當芷帆知道思綸竟然為了她跟自己爽約,又和她獨處到半夜。
芷帆蜷著腿蹲在路燈下,站著的思綸擋住了燈光,卻擋不住她潰堤的淚水。

※
她不敢相信思綸會做出「與前女友獨處到半夜」這種事(我們命名為事件C)。更何況,經過半年的相處,作為理想情人(事件A),思綸的機率已經高達73%。她認為,假如是理想情人,做出事件C的機率應該非常低,了不起最多5%,因此P(C|A)=5%。但要是一個錯的對象,做出這種事情的機率應該是一半一半,P(C|AC)=50%。將這些數字套入貝氏定理
比剛認識時,思綸是理想情人的機率30%還低。這個結果讓芷帆的心沉到谷底。她聽見自己的聲音說
「我們分手吧。」
她不給思綸任何解釋的機會,將自己封閉在家裡,回到臉書大頭貼照裡的那杯咖啡,酸、苦、澀,與甜絕緣。直到介紹的朋友約芷帆吃飯
「我覺得如果是好老公,就不會做出這種讓對方擔心的事情。」
芷帆搖搖頭說,她比誰都想原諒思綸。
但她知道她不會看人,她只能相信貝氏定理的結果。貝氏定理告訴她,思綸是理想情人的機率只有近兩成,她不應該再繼續下去。
「妳太嚴格了,那種情況下,是我也可能會這樣做。因為我相信我女朋友能理解,也會相信我不是會被背叛她的人。」
朋友的男朋友忽然插嘴,朋友點點頭。
「聽說他前女友很情緒化,要是想不開,思綸才真的會一輩子掛念著她。所以他才花那麼多時間安撫她的。」
芷帆動搖了,她又問了其他人,贊成或反對的都有,但整體下來,不如她當初預期的一面倒。因此,儘管芷帆還是認為思綸不是個好老公,才會做出這件事。但她意識到,當初預估的5%機率過低,應該還思綸個公道,修正一下。
芷帆統計眾人的反應,將P(C|A),也就是「給定思綸是理想情人,卻跟前女友獨處到半夜」的機率提高到30%。
芷帆拿出計算機。
幾秒後,芷帆重複檢查,確定式子沒有寫錯。然後,她盯著計算紙半响說不出話
僅僅只是從5%到30%的調整,思綸是理想情人的事後機率,卻從20%提升到62%。儘管比先前的73%下降,但也只下降了11個百分點。
他們之間還是充滿著許多可能。
芷帆將計算結果抱在胸前,慶幸自己有做過這次驗算。這是她第一次發自內心地感謝貝氏定律。貝氏定律讓她有個好理由原諒思綸,讓他們能繼續下去。
芷帆這才清楚自己的感受。就算只有20%的機率思綸會是好老公,或許到最後,她也不會放棄思綸。畢竟真正完美的感情,就算只有那麼1%的機率,也值得一個人費盡一切去追求。

※
「我還以為妳睡著了。」
芷帆回過神來,思綸靠得很近,一張臉佔據了她全部的視線。他的手輕輕掠過她的頭髮。
「你的手指很漂亮。」芷帆握住思綸的手
「是有人說過像金城武的手指,但被這麼讚美,誰會感到開心啊。」
思綸不以為然地說著,回到方才的話題
「那時候,妳後來為什麼決定復合呢?」
「朋友勸我的。」
「哪一位朋友,今天有來嗎?妳沒跟我講,我要好好謝謝他。」
「貝葉斯。」
「啊,外國人?」
註:更多賴以威的數學故事,請參考《超展開數學教室》。