- 作者:吳芳瑜、周盈妤/永春高中
「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2021 數感盃青少年寫作競賽/高中組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
我從高一就加入熱舞社,認識一位二十多歲的舞蹈老師。某次練習時,他說他因為一次空翻失誤,造成了椎間盤突出;後來,聽到一位籃球教練,因長期的運動,也有著椎間盤突出的問題;而身邊也有幾位長輩年輕時經常搬重物,導致了椎間盤突出。
我開始好奇,到底甚麼是椎間盤突出?查了資料才發現,許多從事搬重物的工作者、年輕的運動員,都飽受「腰痛」以及四肢發麻的困擾;而經過檢查發現,這些腰痛及四肢發麻等問題,都是「椎間盤突出」造成的。
有些健康網站或新聞建議了蹲下再搬重物的姿勢,避免造成椎間盤突出問題。而我們試著用簡單的模型,探討這些生活中「不同姿勢對椎間盤所造成的壓力」的問題。
壹、脊椎結構
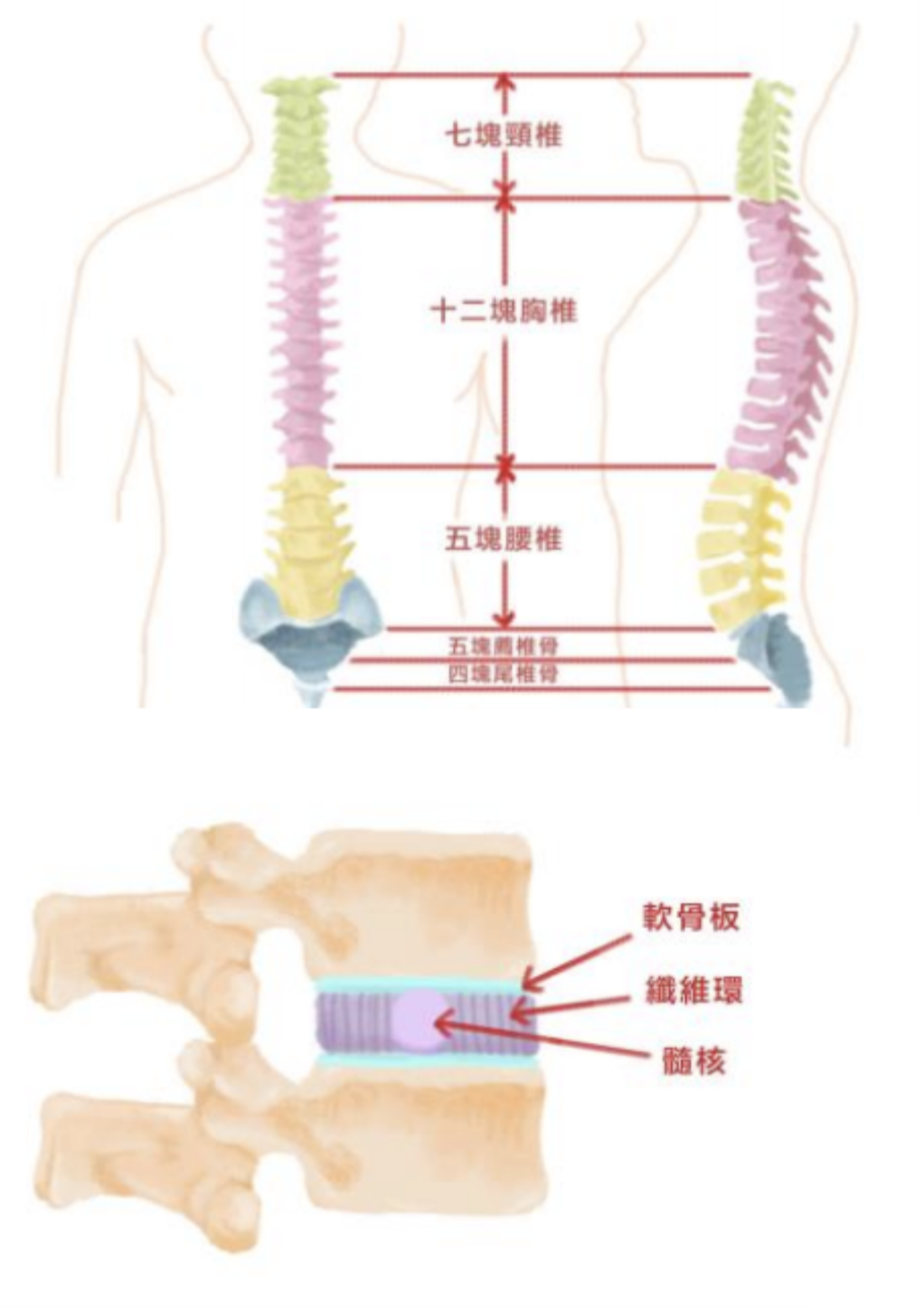
首先,我們先來大致的了解一下脊椎的結構,每個人身上都有 33 塊脊椎骨,分別有 7 塊頸椎、12 塊胸椎、5 塊腰椎、5 塊薦椎、4 塊尾椎。每一節脊椎都會由椎間盤、小關節及韌帶連接。
(一)椎間盤
連接上下兩塊脊椎骨,具有保護、緩衝的功 能,從內到外的結構分別為:髓核、纖維環 、軟骨板(終板),其中髓核是椎間盤最重 要的部分,內部為膠狀物質,可隨外部壓力 改變形狀,負責緩衝的功能。
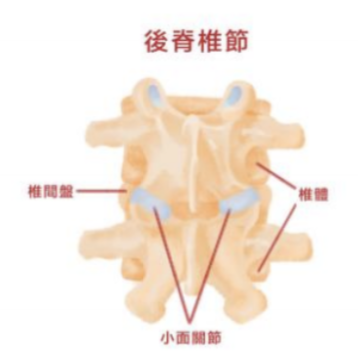
(二)小關節
主要負責穩定兩相鄰脊椎,其表面有相對的軟骨 (作為骨頭的緩衝),周圍有關節滑囊(潤滑)。
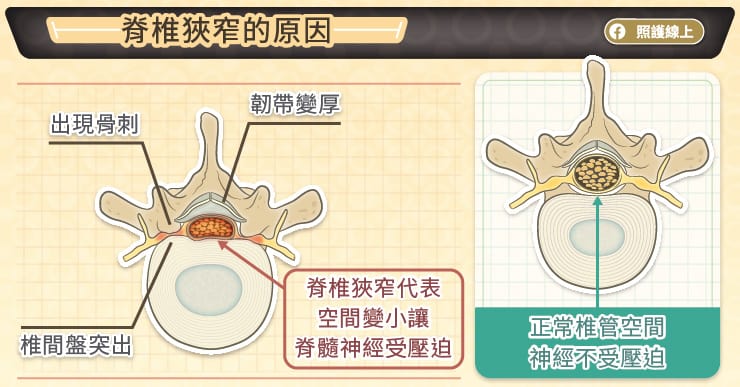
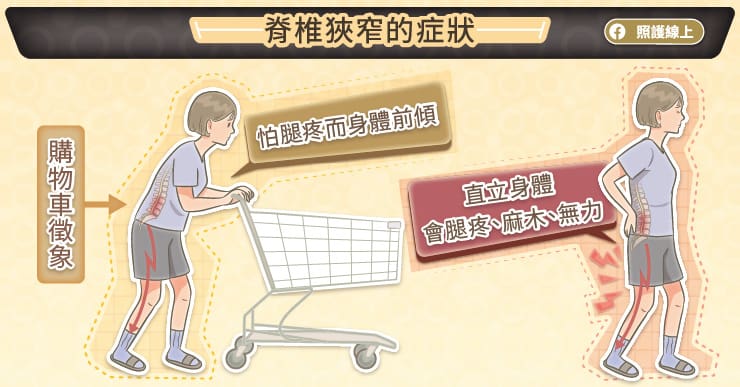
貳、甚麼是椎間盤突出?
俗稱為「椎間盤滑脫」是指位於椎間盤中間、成果凍狀的「髓核」受到擠壓,壓迫到神經、韌帶、脊髓硬膜,或是從外層纖維環的裂縫流出來。大致上可以分成二種情況:
參、椎間盤突出受力分析
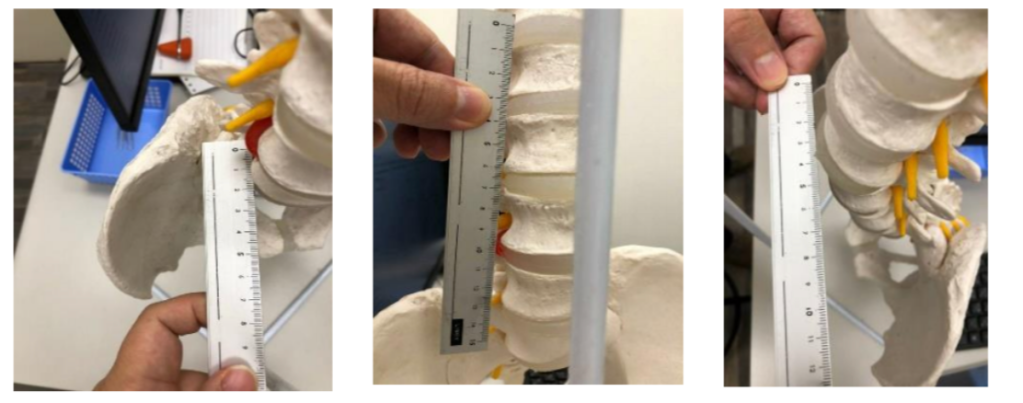
由於我們無法拿實際的骨頭做測量,因此我們詢問生物老師,老師幫我們去保健室取得腰椎模型,得到腰椎長約 3 公分,寬 2 公分,椎間盤間距約為 1 公分。
我們先以長方形的假設對脊椎截面進行討論:脊椎未彎曲時,完整承受正向力的截面積約為 6cm² = 0.0006m²
接下來我們考慮一位身高 170 公分,體重 60 公斤的人,要抬起重量 10kg = 100N 的物體;又假設上半身重量佔全身重量的 75%,則此人上半身重量為 60×75% = 45kg = 4500N
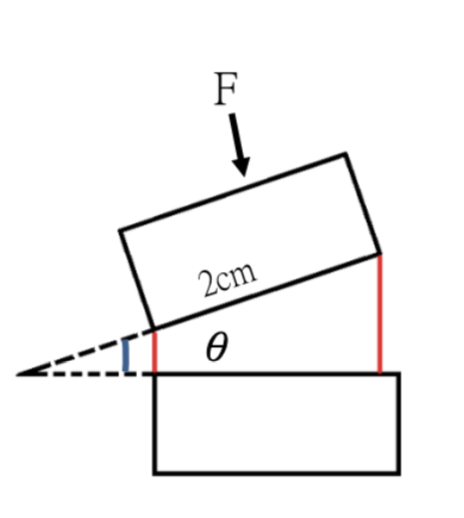
因為多數的椎間盤突出發生在尾椎的位置,所以我們用尾椎第三節及第四節進行討論。如下圖所表示,當我們在彎腰的時候,上方的脊椎對下方脊椎的夾角為 θ,則下方脊椎的垂直受力面積為 2× cos θ × 3(cm2),我們先計算下方接觸面所承受的壓力。
我們會使用正向應力的公式: \( \sigma =\frac{P}{A}(Pa\, or\, N/m^{2}) \)
(一)不彎腰
假設搬重物時,直接下蹲,且脊椎沒有任何彎曲,則此時的彎曲角度為 0°,椎間盤單位面積所承受的力為 (100+4500)÷0.0006=7666666Pa
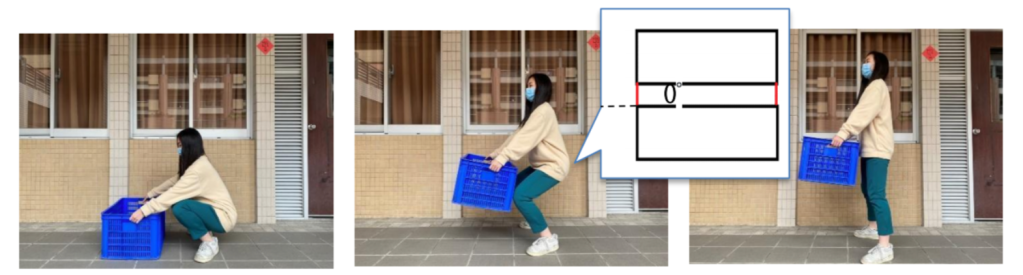
(二)單膝彎腰
假設搬重物時,單膝彎腳下蹲,且稍微彎腰,考慮此時脊椎彎曲角度約為10°,那麼椎間盤單位面積所承受的力為 (100+4500)÷0.0005908=7786052Pa
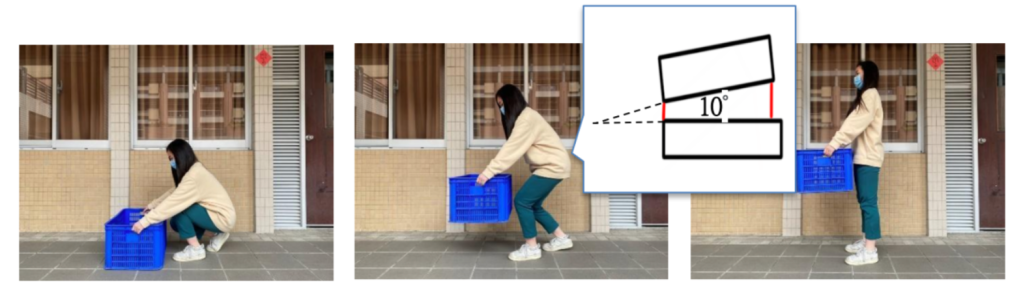
(三)站立彎腰
假設搬重物時直接彎腰,考慮此時脊椎彎曲角度達到最大限度,約為 30°。那麼椎間盤單位面積所承受的力為 (100+4500)÷0.0005196=8852963Pa
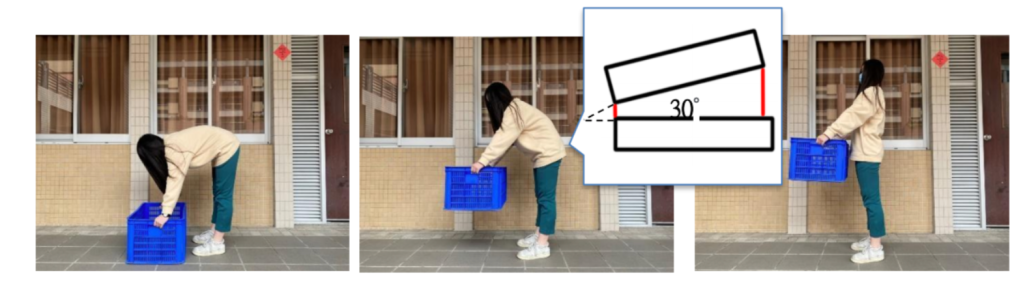
脊椎不同彎曲角度之受力分析
接下來我們進一步考慮椎間盤內部,如下方示意圖。其中 AB 線段從 A 處開始依序通過了纖維環、髓核,再到達前方 B 處的纖維環;C、D 是線段通過髓核的兩側端點;O 是脊髓中點。經剖面圖測量估計, \( \overline{AC}:\overline{CD}:\overline{DB} \) ≒ 1:4:1
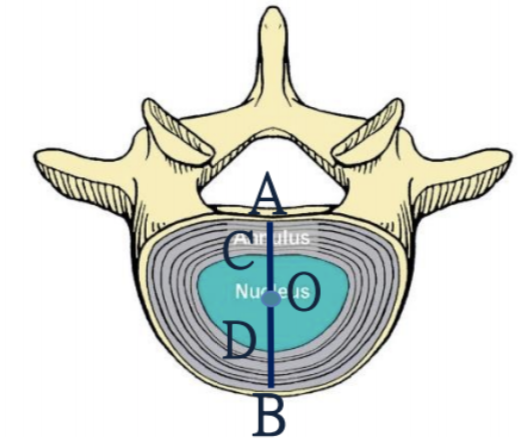
假設上方正向力的大小是 F,在脊椎未彎曲的情形下,也就是 0° 時,受力是平均的,所以每一個部分的平均正向應力皆相同。若有彎曲的狀況,考慮從 A 點到 B 點的範圍,從 0 均勻增加到 2F 的受力分布;在這個狀況下,雖然平均受力仍然是 F,但在 \( \overline{AC} \) 、 \( \overline{CO} \) 、 \( \overline{OD} \) 、 \( \overline{DB} \) 四個對應範圍的正向應力也會有所不同,受力範圍也個別不同。
可推算出各範圍正向力: \( \overline{AC}\approx \frac{F}{6} \) 、 \( \overline{CO}\approx \frac{2F}{3} \) 、 \( \overline{OD}\approx \frac{4F}{3} \) 、 \( \overline{DB}\approx \frac{11F}{6} \) 。
以下是各個對應範圍的正向應力分析:

從上面表格中可以發現,用錯誤的姿勢搬重物,對於纖維環的壓力甚至可能達到正確姿勢的 \( \frac{21153}{1666}\approx 13 \) 倍以上!
在一開始討論的例子中,F 的值是 4600N,水深增加 1m,壓力大約就增加 101.3hPa,所以 m=xF÷100÷101.3hPa,換算出這些壓力對應到在海裡大約是多少深度:

肆、結論
由上表得知當脊椎彎曲 30° 時, \( \overline{DB} \) 部分纖維環所承受的壓力是 0° 時的 13 倍,且超過了 人體極限的 32 倍(人類自由潛水最深紀錄為 300m),換算成海的深度就接近世界上第六深的海溝——克馬德克海溝(深度約 10047 m)的底部,難怪對椎間盤會造成這麼大的傷害!
所以我們要用正確的姿勢搬重物,對椎間盤造成的傷害也會大幅的降低,透過這次的數學模型分析,我們才了解到錯誤的動作會對椎間盤承受的壓力有多大,因此希望大家好好保護自己的脊椎,不要再直接彎腰下去拿重物了!
引注資料:
- 《腰痛》/長谷川淳史
- 《背部保健學習百科》/John Tanner
- 頸/脊椎的結構與功能
- 應變 Strain & 應力 Stress (原文的連結有誤)
- 脊椎生物力學 (原文的連結有誤)