- 作者/Steven Strogatz,本文摘自《無限的力量》,旗標出版,2020 年 09 月 09 日

在進入細節之前,讓我先說明一下本節中要做的事情。首先,在心中描繪一個圓形的物體,比如說一塊披薩。然後,藉由將這個披薩切成無限多塊並重新排列後,可以神奇地重新組合成一個長方形。因為重組排列切片並不會改變披薩的面積,同時我們也曉得如何求長方形的面積(只要將它的長與寬相乘即可),因此藉助這個策略,就能得到我們想要的答案:一個可以計算圓面積的公式。
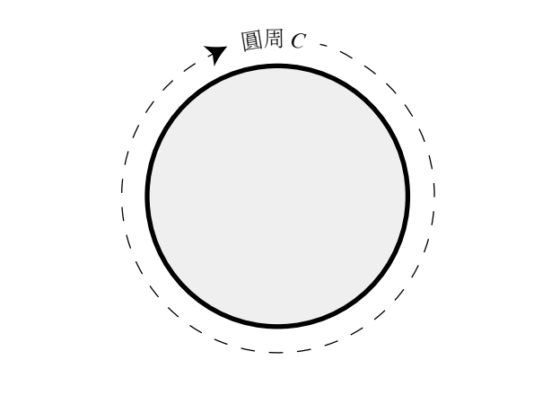
為了使上述步驟得以順利進行,我們以英文字母 C 代表圓的周長(披薩最外緣的長度),我們可以用捲尺繞行披薩一圈來測得 C 的值。
另一個我們需要知道的數據是披薩的半徑長度,記做 r,它的定義是從披薩中心到邊緣上任意一點的長度。另外,假如所有的披薩切片都一樣大,且切法都是從中心往邊緣切,那麼 r 就是一塊披薩切片的側邊長度。
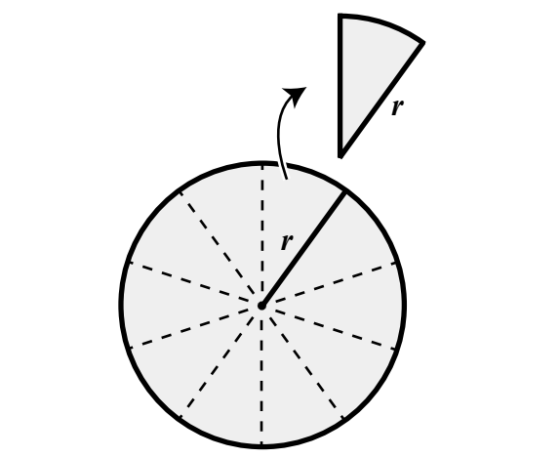
我們先將披薩平分成四小片,並把切片重新排列成以下圖形。很顯然地,結果不盡如人意。
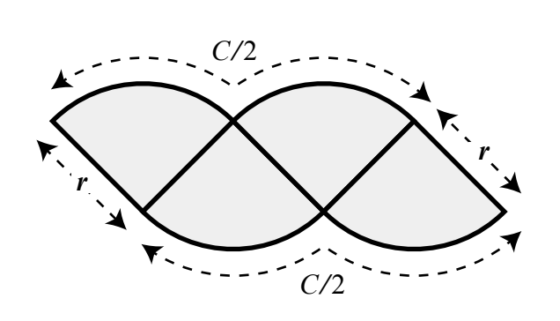
這個新形狀的頂部與底部都是波浪狀的,整體看上去就奇形怪狀。總而言之,這絕對不是一個長方形,因此我們也無法輕易猜到它的面積。這樣看起來,似乎沒有什麼用啊!不過正如所有的電影一樣,英雄在成功之前總是要經歷一些麻煩,此處的失敗也只是在為我們的探索過程增加一些戲劇張力罷了。
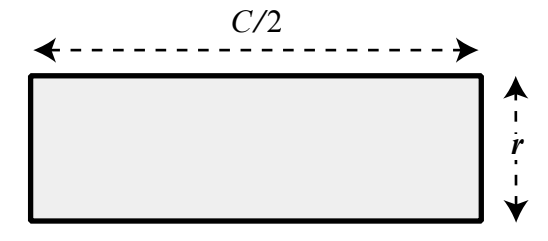
然而,在我們進到下一步之前,有兩個事實應該特別指出來,因為在我們的證明裡,它們自始至終都正確。這第一項事實是:新圖形頂邊與底邊的長度都恰好是周長的一半,也就是 \(\frac{C}{2}\)(如上圖所示),而我們所求四方形的長邊長度最後就會等於這個值。第二項事實是,圖形中那兩條傾斜的側邊剛好是一片披薩切片的側邊,因此長度就是 r,且這個長度最後會變成所求四方形的短邊長度。
在上面的操作中,我們之所以看不到任何四方形的影子,是因為這塊披薩還沒被切成足夠多片。如果這一次我們將它平分成八等分,並以相同的方式將切片重排,得到的新圖形就會離四方形的樣子更接近一些。
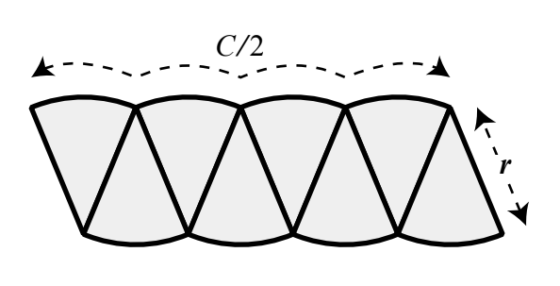
事實上,重排過後的披薩開始看起來就像是一個平行四邊形(parallelogram)。這結果還不賴,至少圖形頂部與底部那類似波浪的結構也不像之前那麼凹凹凸凸。如此可見,隨著切片數量增加,整個圖形看起來也會越平坦。要注意的是,圖形頂部與底部波浪狀的地方長度仍然是 \(\frac{C}{2}\),而兩端傾斜側邊的長度也依舊是 r。
為了讓我們的圖形看起來更工整,還可以把最左邊或最右邊的披薩切片再切成一半,並把切下來的半片拼到另一邊去。
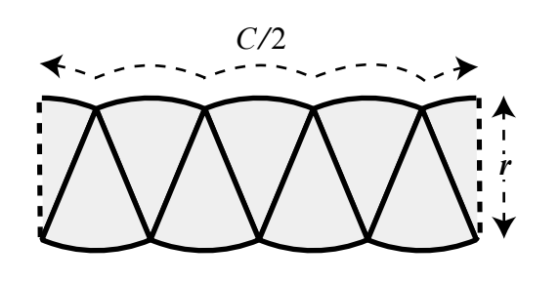
現在,整個圖形看上去就更像一個長方形了。當然我們得承認,目前的結果還不夠完美,因為圖形的上下方還是波浪狀的,但至少已經有些進展。
既然增加切片的數目看似對解題有幫助,那就讓我們繼續切下去吧!這一次新圖形是由十六片披薩切片所組成,同時,我們再次對它的側邊進行類似上面的切半搬移處理。最後的結果看起來如下:
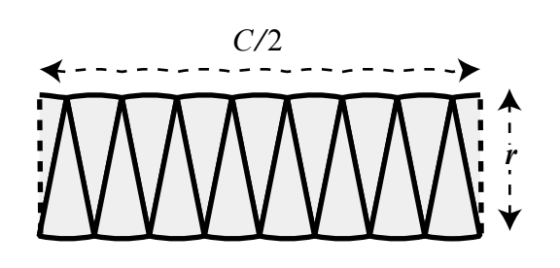
總的來說,將披薩平分成越多片,原本波浪狀的部分就變得越平坦。我們可以看到,經過處理後,一系列新的形狀誕生了!而且很神奇地,這些形狀看起來越來越接近方方正正的四方形(即長方形)。由於此四方形是將披薩平分無數次之後的結果,我們就把這個四方形稱做「極限(limiting)」四方形吧!
編註:我們前面談過很多的「無限(infinity)」是一種趨近的過程,而「極限(limiting)」則是指此趨近過程最終所達到的狀態。比如說:「無論你到天涯海角,我都要追上你」其中,永無休止追的過程是無限的概念,而追到天涯海角時就是那個最終的極限狀態。
前面所做的這一切,就是為了得到這個極限四方形,好讓我們能簡單地透過長乘以寬來算出面積,而剩下來的任務就是找出這個極限四方形的長寬和原本的圓之間存在什麼關係了。
首先,由於組成極限四方形的每一片披薩切片都是由披薩中心切出來的,因此四方形的短邊長度就是原本的圓半徑 r。至於四方形的長邊長度則等於圓周長的一半,這是因為有一半的周長被分配到了四方形的頂邊,另一半則被分配到了底邊。也就是說,長邊的長度等於 \(\frac{C}{2}\)。結合以上兩點,我們便可透過將長邊乘以短邊來得到極限四邊形的面積(以 A 表示),即 \(A = r\times \frac{C}{2} = \frac{rC}{2}\)。最後,因為搬動披薩切片並不會改變它的面積,所以此極限四邊形的面積一定等於原始的圓面積!
以上所得的圓面積公式 \(A = \frac{rC}{2}\) 是由古希臘數學家阿基米德(Archimedes,公元前 287 – 212 年)在他的文章《圓的測量》中首次證明的(他用了類似但更加嚴謹的論證)。
這個證明最創新的部分在於如何運用無限這個概念來協助我們得到答案。當我們只有四片、八片、或十六片披薩時,只能將它們重排成一個波浪狀的不完美圖形。然而,儘管開頭並不順利,隨著切片數不斷增加,我們所得到的圖形也越來越接近長方形。不過這裡必須注意,只有當切片數量達到無限多片時,重組之後的圖形才會完全變成長方形。而這就是微積分背後的關鍵想法:當到達無限以後,所有事情都會變得簡單!