- 作者/Steven Strogatz,本文摘自《無限的力量》,旗標出版,2020 年 09 月 09 日
微積分傳統上都是被應用於「硬」科學上,諸如:物理、天文、以及化學等。但在最近的幾十年裡,它的觸角已經伸入醫學與生物學的領域中,如:流行病學(epidemiology)、族群生物學(population biology)、神經科學(neuroscience)以及醫學影像技術。在之前介紹過的故事裡,我們已經看過好幾個生物數學的應用實例了,從利用微積分預測面部手術的效果,到模擬 HIV 和免疫系統間的戰鬥都有。但以上所有例子都和某種變化有關,而這也是現代微積分最大宗的運用所在。與此相反,我們接下來要講的案例則源自於古老的彎曲之謎,只是被 DNA 的三維結構問題賦予了新的生命。

這個案例和 DNA(一種非常長的分子,其上包含了構成一個人所需的所有遺傳訊息)如何被包裝收納於細胞中有關。在你身上將近幾十兆個細胞內都存在著一條長度大約兩公尺的 DNA。若你將這些 DNA 全部頭尾相接,則其總長度足夠在地球和太陽之間往返好幾回。到此,有些人可能認為這沒什麼了不起的,不過是因為我們身上的細胞數量太多了而已。那就再來看另一組更有意義的比較吧:讓我們考慮一個細胞核(nucleus;裝載 DNA 的容器)有多大。
一般來說,一個細胞核的直徑約莫為五百萬分之一公尺;也就是說,它比儲存在其中的 DNA 分子小了四十萬倍。以巨觀的東西來比喻,那就相當於將一條二十英里長的繩子塞到一顆網球的內部一樣。
除此之外,DNA 可不能被隨便亂塞到細胞核中。它不可以纏在一起,因為 DNA 必須被酵素讀取才能轉譯成維持細胞活動所需的蛋白質。與此同時,有規律的包裝也才能保證細胞在分裂時,DNA 能夠被順利地複製。
演化對於這個問題的答案是使用類似於線軸的結構,這和我們收藏長線段的方式很像。在細胞內,DNA 會被纏繞在一種由組織蛋白(histones)構成的分子線軸上。為了再進一步讓結構更緊密,這些分子線軸彼此之間也會相連,就像項鍊上的串珠一樣。然後,這條如項鍊一般的構造還會捲成一根類似於繩子的纖維,而這些纖維則再捲成被稱為染色體的結構。這種三重捲曲的收納方式能將 DNA 變得很小,小到足以被塞到細胞核中的某個角落裡頭。
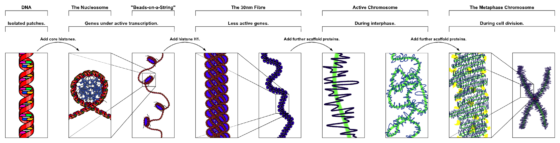
然而,線軸結構其實並不是大自然對此一問題最初的解決方法。地球上最早的生命體是一群沒有細胞核和染色體的單細胞生物。正如今天的細菌和病毒一樣,它們也沒有之前提到過的線軸,其遺傳物質的壓縮是透過一個和幾何與彈性有關的機制來完成的。
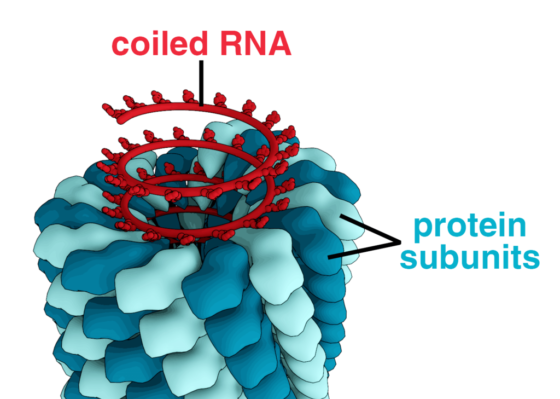
請想像一下,你將一條橡皮筋握於兩手手指之間並拉緊,接著從某一端開始扭轉它。一開始,橡皮筋每轉一圈就會產生一個交叉;這些交叉的數量會不斷累積,但橡皮筋本身還是保持一直線的,直到整個系統承受的扭力超過了一個閾值為止。一旦超過了閾值,該橡皮筋便會開始產生一些三維的扭結。它會自我收縮扭曲,就像在痛苦中掙扎一樣,由此產生的扭轉可以使橡皮筋最後縮成一顆緊密的球。而早期生命體的 DNA 便是以類似這樣的方式收納的。
以上現象被稱為超螺旋(supercoiling),它在環狀的 DNA 上很常發生。雖然我們平常都把 DNA 想成是一條筆直、具有兩個端點的螺旋結構,但在某些場合中它的兩端也會互相連接起來形成一個圓。當這種情形發生時,整條 DNA 的狀況就會像是你將皮帶從腰上解下來,扭個幾圈,然後再扣回去一樣。注意!一旦皮帶被重新繫回腰上,那麼它扭轉的圈數也就固定無法改變。在這種狀態下如果你還想在皮帶某處多扭一圈,那麼另一處就勢必會產生一個相反方向的扭動來抵消這個新的改變,就好像有某種守恆定律在運作一樣。另外,當你把一條花園水管一圈疊一圈地盤繞在地上時,相同的事情也會發生:在把水管拉直的同時,它會在你的手中扭動。在上述現象中,螺旋化成了扭轉。而事實上,這種扭轉也有可能反過來化成螺旋,如同橡皮筋隨著被扭曲而不斷盤繞一樣。原始生物的 DNA 也利用了這種盤繞。在它們的體內有某種酵素可以切斷 DNA 分子,將其扭個幾圈,然後再把分子重新接上。隨後,當 DNA 試圖釋放身上的扭轉以降低自身的能量時,之前提過的守恆定律便會讓它產生超螺旋,並進而縮得更加緊密。最後,這些生物的 DNA 分子將不再是一個平面物體,而是纏繞成了一個三維的構造。
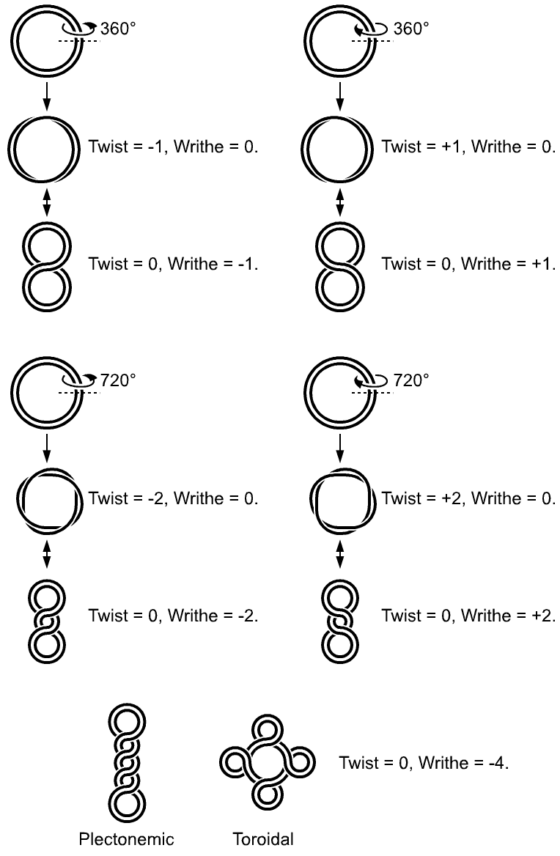
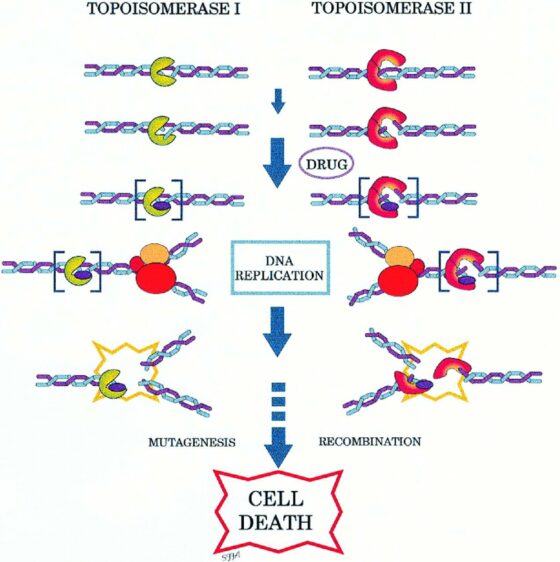
1970 年代初的時候,一位名為布羅克‧富勒(Brock Fuller)的美國數學家給出了第一個 DNA 三維扭曲的數學描述。他發明了一種命名為 DNA 纏繞數(writhing number)的指數。不僅如此,他還利用積分與導數推導出計算公式,同時證明了在纏繞數中存在著和扭轉與螺旋有關的守恆定律。自那以後,對於 DNA 分子的幾何與拓撲學研究開始興起。一些數學家使用了紐結理論(knot theory)與纏結微積分(tangle calculus)去解釋特定酵素切斷 DNA、或使其扭轉、又或者在其上製造紐結後再重新將其黏合起來的機制。由於這些酵素會改變 DNA 的拓撲構造,因此它們又被稱為拓撲異構酶(topoisomerases)。此類酵素可以將 DNA 的雙股切斷並再次接起,因此對於細胞的分裂和生長是很重要的。
與此同時,它們也被證實是癌症化療藥物的有效作用目標。雖然這背後的藥理機制還不是很明確,但根據猜想,這些被稱為拓撲異構酶抑制劑(topoisomerase inhibitors)的藥物,能藉由使拓撲異構酶失去活性來選擇性毀損癌細胞的 DNA,並進一步促使這些細胞自殺。這對於病患來說是一大福音,但對於腫瘤細胞來說則是一大噩耗。
在微積分對 DNA 超螺旋的應用中,DNA 分子的雙螺旋結構被假設成了一條連續的曲線。因為正如之前一樣,微積分還是比較擅長處理連續物體的。但在現實中,DNA 並非真的連續,而是一群離散原子的集合。只是在一定的程度上它可以被近似地當作一條連續曲線,如同一條理想的橡皮筋那樣。這麼做的好處是:如此一來,彈性理論(elasticity theory)和微分幾何(differential geometry)這兩門微積分分支就能被應用於 DNA 之上,進而計算出該分子如何因為蛋白質的外力、環境的影響、和與自己的互動而改變形狀。
從更宏觀的角度來說,在此問題上微積分採取了它慣用的作法,即透過將不連續的物體假定為連續來揭露它們的行為。這樣的模擬雖然只是趨近,但它很有用。或者說,它是我們唯一的選擇。因為要是沒有了這個連續性的假設,那無限原理就毫無用武之地,而一旦無限原理失效,微積分、微分幾何和彈性理論也就不復存在了。
預期未來我們將會看到微積分和以連續為前提的數學,被應用在更多離散的生物學實體上:基因、細胞、蛋白質、以及生命舞台上的其它成員。藉由這種連續性的假設,我們能獲得太多資訊了。因此,直到我們發展出一套對離散系統也同樣有效的微積分以前,無限原理仍會是我們以數學模擬生命現象時的指導原則。



















《運動基因》立體封面72dpi.jpg)



















-200x200.jpg)