二十世紀是人類史上科學技術進展最快的世紀。短短的 100 年間,湧現了大量對世界產生重大的影響的科學發現和技術突破,包括電視、飛機、抗生素、基因科學、量子力學……。
但若要評選一項滲透至人們日常生活的所有角落、改變人類生活型態最劇烈的科技發明,則非電腦 莫屬。
第一次工業革命是機械與工廠、第二次工業革命是電力、第三次工業革命乃由電腦發明所激起的資訊時代。有著「第四次工業革命」之稱的人工智慧,我們已在深度學習簡史中有所探討。但追本究源,人工智慧所奠基的電腦(計算機)科學,又是怎麼來的?
今天就讓我們來思考一個有趣的問題:電腦是怎麼來的?
ENIAC:情人節誕生的奇蹟
普遍認為最早的通用電腦,是美國賓州大學的莫奇來 (Mauchly)和他的學生埃克特 (Eckert)在 1946 年 2 月 14 日情人節當天所發表的「ENIAC」 。(情人節剛過不久但別再討論單身魯了,人家可是在情人節顛覆世界呢 XD)
ENIAC 計算機在進行每一次運算之前,都須根據運算要求、把不同的元件用人工插接線路的方式連接在一起。將輸入裝置和輸出裝置設好後,才進行通電……啪!一聲,電腦噠噠噠的開始運作。
但現在可能正用電腦看這篇文章的你,好像不需要在開機前把電線插來插去才能使用? 因為這個電路沒有儲存程式的功能。最早的計算機器僅內涵固定用途的程式,比如一台「計算機器」僅有固定的數學計算程式,除此之外便無其他,無論是文書處理或玩遊戲都不行。若想要改變這台機器的程式,你必須更改線路、結構甚至重新設計機器。
馮.紐曼結構與現代電腦
1945 年 6 月,是現代電腦科學的里程碑。著名的美籍猶太裔數學家馮.紐曼 (John von Neumann) 與多位學者聯名發表了一篇長達 101 頁的報告,其中包括大膽捨棄了十進制、改以二進制運算取代,同時將電腦明確分成五個部分組成(包括:記憶體、控制單元、算術邏輯單元、輸入 / 輸出裝置等),並描述了這五個部分的功能和相互關係,為電腦的邏輯結構設計奠定了基礎。
事實上,EDVAC 報告中最核心的概念即是「可儲存程式的電腦 (Stored Program Computer) 」。如果是一台能儲存程式的電腦,只要一開始先將「文書程式」與「遊戲程式」都載入記憶體中,再告訴電腦去記憶體的哪一個位置開始執行就可以完成,在不需更動硬體的情況下就能讓電腦變得更加有彈性。
1951 年,美國軍方透過馮.紐曼的協助,斥資五十萬美元打造了計算機「EDVAC」。相較於十進位、又須人工插接電路的 ENIAC,可以說 EDVAC 是第一台現代意義的通用計算機,直至今的現代電腦皆仍採用馮.紐曼架構。
在我們介紹馮.紐曼其人其事、與現代電腦的運作原理前,先讓我們重看一次標題所提出的問題:「電腦是怎麼來的?」為什麼馮.紐曼能夠造出這樣的一台電腦?
不少人把馮.紐曼當作是電腦科學的奠基人,有人甚至稱他為「電腦之父」。然而他本人並不接受這個稱號。
馮.紐曼認為他的研究成果是受到了英國數學家圖靈 (Alan Turing) 所啟發,他僅僅是發揚光大圖靈的原始概念。這台「可儲存程式電腦」真正的意義,其實就是通用圖靈機。馮.紐曼將這個概念的創始人公正無私地還予圖靈。
圖靈:可計算理論與圖靈機
好吧這麼來看,如果我們想要瞭解「電腦是怎麼來的?」,勢必得再先去瞭解圖靈這位同樣有著「電腦科學之父」與「人工智慧之父」之稱的偉大學者,與其圖靈機 (Turing Machine) 的理論了。
1934 年,年僅 22 歲的圖靈從劍橋大學畢業、到美國普林斯頓大學攻讀博士學位。二戰爆發後,圖靈在 1939 年被英國皇家海軍招聘,協助軍方成功破譯德國的密碼系統 Enigma,讓英國軍方對德國的軍事計劃瞭如指掌。圖靈小組的傑出工作,更使得盟軍提前至少兩年戰勝納粹。
--上述是電影《模仿遊戲》的史料。對於圖靈生平有興趣的讀者,可以參考這部向圖靈致敬的電影。 (只是嚴防許多出錯的史實) 除了作為一位傑出的密碼學家,在電影沒詳述的部分中,圖靈在電腦科學上的貢獻更是難以抹滅。
1936 年,24 歲的圖靈發表了一篇論文《論可計算數及其在判定問題上的應用》(On Computable Numbers, with an Application to the Entscheidungsproblem)。在這篇極富開創性的論文中,圖靈提出了「圖靈機」 (Turing Machine) 概念。
「圖靈機」不是一台具體的機器,而是一種運算模型,可製造一種十分簡單但運算能力極強的機械裝置,用來計算所有能想像得到的可計算函數。
圖靈機是闡明現代電腦原理的開山之作,奠定了整個電腦科學的理論基礎。如果說馮紐曼是實際打造出一台現代電腦的電腦之父,其所依據的理論基礎即源自於圖靈機。
但,什麼叫可計算?為什麼圖靈會探討這個問題?實際上,上述關於圖靈論文與圖靈機的介紹,更明確的說法應是:圖靈在 1936 年發布的論文中,對於「哥德爾不完備定理」重新做了論述。相較於哥德爾在證明其不完備定理時、採用的通用算術形式系統,圖靈使用了叫做「圖靈機」的簡單裝置作為代替。
咦,我們這邊又多提到一個人了?!哥德爾……?
哥德爾不完備定理
哥德爾 (Gödel) 被譽為自亞里士多德以來、歷史上最偉大的邏輯學家 之一。毫不誇張地說,正是哥德爾使數理邏輯與哲學界發生了極大的革命。
愛因斯坦曾說:我之所以還到研究院來,只是為了與哥德爾一起走路回家。 1931 年,19 歲的圖靈進入劍橋大學就讀;但這一年,同時成了撼動數學界的里程碑——奧地利數學家哥德爾提出不完備定理,證明不存在既完備又一致的數學體系,粉碎了無數位數學家追求聖杯的野心。
人類總是渴求著確定的知識,也稱為真理 ——藉由純數理論與邏輯證明,數學家不斷尋找著真理的可確定性。
哥德爾當年的發現,簡單來說是:「並非所有為真者,皆可循一邏輯演繹過程而得知」 。再更直白點就是:「真理的範圍、比我們所能證明的範圍還大。」
數學家乃藉由公理(不證自明、理所當然為真的命題)進行一連串的推理、最後得出數學定理;基本上是活在一個以邏輯演繹為本質的世界。今天突然有人成功證明了:有些數學命題,我們既沒辦法證明它為真,也沒辦法證明它為假……,可想而知,這對於數學界無非是一項沈重的打擊!
五年後的圖靈之所以提出「圖靈機」計算模型,即是以計算機的形式重新演繹了哥德爾的不完備定理,同時補充了判定問題--是否存在一個程式,能判斷:我們任意輸入的一個程式,是否能在有限的時間內結束步驟?或者會陷入無窮迴圈?(當我們對電腦下兩個指令:【往左後往右】與【往右後往左】,電腦就會陷入無窮的迴圈)
哥德爾的發現,引起了當時重要數學家如希爾伯特與馮.紐曼(還記得這個人嗎? 這位計算機之父早年是希爾伯特的助手)等人的重視。到後來不但啟發了後續眾多數學家、哲學家:若無法使用邏輯演繹完全瞭解宇宙,該何以為繼? 更激起圖靈創造出了電腦科學在理論上的濫觴。
但是,為什麼哥德爾會探討這樣的問題呢?因為有人下了戰帖!
誰?就是上上句我們提到的大數學家希爾伯特!
希爾伯特的 23 個問題
希爾伯特 (David Hilbert) 是二十世紀初期德國最偉大的數學家之一。
在世紀之交的 1900 年、一場巴黎國際數學家大會的演講當中,希爾伯特根據 19 世紀的研究成果和發展趨勢,以卓越的洞察力提出了 23 個當時尚未被解開的困難數學問題,並鼓舞年輕數學家積極攻克:
「在我們中間,常常聽到這樣的呼聲:這裡有一個數學問題,去找出它的答案!你能通過純思維找到它,因為在數學中沒有不可知。」(希爾伯特大大按曰:只要解出來就能名留青史噢!)
這就是著名的希爾伯特的 23 個問題。
希爾伯特的 23 個問題對 20 世紀的數學研究起了積極的作用,不但超乎希爾伯特的預期,更未曾預料到從其中衍生而出的電腦科學、將會對世界產生無比重大的影響。
而哥德爾之所以提出不完備定理,想解答的正是這 23 個問題中的第二個問題:算術公理系統的無矛盾性。簡單來說,希爾伯特希望能以一個完美的形式系統,成功證明所有的真理、同時找出所有矛盾的陳述。
在這個問題上,希爾伯特原先堅定地表示:「沒有人能將我們逐出康托爾的樂園。」不僅僅是第二個問題,希爾伯特在 23 個問題中所提出(顯然最在意)的第一個問題連續統假設,也是康托爾的研究中所面臨問題。
康托爾……?請放心,這會是本篇文章中所出現的最後一位人名了。
無限多的危機:康托爾集合論
到目前為止,我們已經使用了許多強烈的形容詞,包括:電腦科學之父、偉大的邏輯學家、數學家……。但在這些學者的研究基礎上,我們不能不提現代數學的奠基者——集合論之父康托爾 (Cantor) 。
令集合 A = {1, 2, 3, 4, 5 },B = {1, 3, 5, 7, 9}
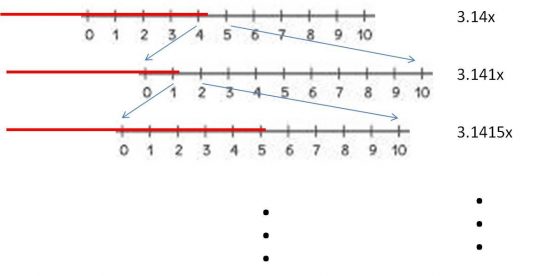
康托爾可以說是數學史上最富有想像力的數學家之一,其所開創的集合論則可以說是人類最偉大發明之一--當年康托爾面臨的,正是數學界幾百年幾千年的疑懼:「無限」。
1-1+1-1+1… = 0, 1 還是 1/2? 0.99999….. = 1?還是 <1?
無限有多大?正整數、整數 (正整數 / 負整數 / 0)、實數(有理數 / 無理數) ……等數系的數量相同嗎?
Z+: ∞ (正整數有無限多個), Z-: ∞ (負整數有無限多個), Z: ∞ (整數有無限多個)。
為了處理「無限」這個長久得不到解決的難題,康托爾在 19 世紀下半葉創立了「集合」理論,證明了各個數系雖然是都是無限多,還是有數量上的差別:
| 正整數 | = | 整數 | = | 有理數 | < | 無理數 | = | 實數 | = | 複數 |
無限多的正整數數量 = 無限多的整數數量 = 無限多的有理數數量 < 無限多的無理數數量 = 無限多的實數數量 = 無限多的複數數量
然而集合論實在太過創新、對於無限的解釋也背離了傳統,剛開始時康托爾受到了嚴厲的譴責與撻伐。
但隨後,許多年輕的數學家開始意識到集合論非常的有用--基於自然數 (正整數)與集合論,當時一切的數學成果都可以成功被推證出來。
1900 年在國際數學家大會上,法國數學家龐加萊興高采烈地宣稱:「藉助集合論,我們可以建造起整個數學大廈。」1925 年,希爾伯特也提出了「希爾伯特旅館悖論」來應和康托爾的理論。
然而康托爾集合論仍然面臨了許多問題。首先是連續統假設--我們已知:
| 正整數 | = | 整數 | = | 有理數 | < | 無理數 | = | 實數 | = | 複數 |
始終證明不出問題、又受到世人無數攻訐的康托爾,晚年發了瘋、死在精神病院中。
但除此之外,集合論還有一個問題是羅素悖論:「這句話是假的。」讀者只要稍加推論就會發現:如果這句話是真的,那麼這句話是假的會成立……?!如果這句話是假的,那這句話就是真的……?! 這個命題就矛盾了。
羅素悖論應用在集合論的問題即是:如果我們創造一個集合 A,裡面收集了所有不包含在自己這個集合的集合:A = {x|x∉x}。若是 A∈A 成立,則 A 是 A 的集合、使得 A∉A。但若 A∉A,則符合命題,使得 A∈A。
好不容易我們在集合論的基礎上構築起了數學大廈,結果發現集合論也是不完美的。究竟能不能找到一個完備的系統,從上面建築起整個數學的基礎呢?
這樣的系統是否存在呢?希爾伯特除了在 23 個問題中的第一個問題提出「連續統假設」,身為康托爾堅定的擁護者(腦粉),也在第二個問題中提了這樣的難題。
這也接續到我們先前的介紹:再後來哥德爾成功證明了不完備定理、解決了 23 個問題中的第二個問題,到圖靈用「圖靈機」的概念更加簡單明瞭的重新演繹一次哥德爾不完備定理,最後馮.紐曼基於通用圖靈機的概念、建出了第一台具備現代電腦架構雛形的電腦。
哇!「電腦是怎麼來的」居然爬梳出這麼多的問題?
哲學:不懈探究真理的精神
若要探究下去,你知道:康托爾、希爾伯特、哥德爾、馮.紐曼…等人都是德國人嗎(哥德爾和馮.紐曼皆為奧匈帝國人)?19 世紀的德國究竟是一個什麼樣的時代,造就了如此多的數學大家?
事實上,你知道這些數學家同時還有著哲學家的頭銜嗎?更進一步來說,19 世紀知名德國哲學家,尚包括了:黑格爾、叔本華、馬克思、尼采、康德… 毫無疑問地,當時的德國可說是歐洲最具代表性的哲學重鎮。
哲學反映了人類對真理的追求,體現人類的智能與認知極限。因而數學的發展不只是解一些生活問題,而成為一種學問、一種探求真理的道路與哲學手段。 哲學在西方文化中扮演了非常重要的角色,也是現代科學會出現在歐洲的重要原因。至於西方哲學追求真理的精神,又是起源於何時何處呢?這又要回溯到希臘時期,比如亞里斯多德的三段式證法或畢達哥拉斯學派……。
觀察過往,出現像上述「無限有多大」這樣的數學危機,在人類史上也不是第一次發生了:負數的英文為--Negative Number、無理數--Irrational Number、虛數--Imaginary Number。否定的 (Negative)、不合理的 (Irrational)、想像的 (Imaginary)……。
從這些詞彙中可以看出在探究真理的過程中,人類總是不斷遭遇思想上的困難,卻又能在突破後、成功踏上嶄新的道路。 今天我們思考了一個問題:「電腦是怎麼來的?」,並從中衍生出了更多值得探索的問題:
.數學是邏輯、也是哲學?
沒有了探求宇宙真理的精神,或許工業革命就不會出現在歐洲了? 人類也不會有科技發展、或者今日的生活。
少年啊,你渴望真理嗎? 後續幾篇,我們會繼續用深入淺出的方式一一來討論這些問題,歡迎一起加入這樣的思考訓練吧!
本文轉載自寫點科普,請給指教。 《電腦是怎麼來的?(思考訓練)》 ,歡迎贊助和訂閱Lynn的網站喔。