《跟孫臏比一場賽馬吧！》——2018數感盃 / 高中組專題報導類第二名

本文與 美商德州博藝社科技 HEART 合作，泛科學企劃執行。

提到台灣令人焦慮的交通，多數人會想到都市裡的壅塞車潮，但真正致命的「塞車」，其實正悄悄發生在我們體內的動脈之中。

這場無聲的危機，主角是被稱為「壞膽固醇」的低密度脂蛋白（ Low-Density Lipoprotein，簡稱 LDL ）。它原本是血液中運送膽固醇的貨車角色，但當 LDL 顆粒數量失控，卻會開始在血管壁上「違規堆積」，讓「生命幹道」的血管日益狹窄，進而引發心肌梗塞或腦中風等嚴重後果。

科學家們還發現一個令人困惑的現象：即使 LDL 數值「看起來很漂亮」，心血管疾病卻依然找上門來！這究竟是怎麼一回事？沿用數十年的健康標準是否早已不敷使用？

膽固醇的「好壞」之分：一場體內的攻防戰

膽固醇是否越少越好？答案是否定的。事實上，我們體內攜帶膽固醇的脂蛋白主要分為兩種：高密度脂蛋白（High-Density Lipoprotein，簡稱 HDL）和低密度脂蛋白（ LDL ）。

想像一下您的血管是一條高速公路。HDL 就像是「清潔車隊」，負責將壞膽固醇（ LDL ）運來的多餘油脂垃圾清走。而 LDL 則像是在血管裡亂丟垃圾的「破壞者」。如果您的 HDL 清潔車隊數量太少，清不過來，垃圾便會堆積如山，最終導致血管堵塞，甚至引發心臟病或中風。

因此，過去數十年來，醫生建議男性 HDL 數值至少應達到 40 mg/dL，女性則需更高，達到 50 mg/dL（ mg/dL 是健檢報告上的標準單位，代表每 100 毫升血液中膽固醇的毫克數）。女性的標準較嚴格，是因為更年期後]pacg心血管保護力會大幅下降，需要更多的「清道夫」來維持血管健康。

相對地，LDL 則建議控制在 130 mg/dL 以下，以減緩垃圾堆積的速度。總膽固醇的理想數值則應控制在 200 mg/dL 以內。這些看似枯燥的數字，實則反映了體內一場血管清潔隊與垃圾山之間的攻防戰。

那麼，為何同為脂蛋白，HDL 被稱為「好」的，而 LDL 卻是「壞」的呢？這並非簡單的貼標籤。我們吃下肚或肝臟製造的脂肪，會透過血液運送到全身，這些在血液中流動的脂肪即為「血脂」，主要成分包含三酸甘油酯和膽固醇。三酸甘油酯是身體儲存能量的重要形式，而膽固醇更是細胞膜、荷爾蒙、維生素D和膽汁不可或缺的原料。

這些血脂對身體運作至關重要，本身並非有害物質。然而，由於脂質是油溶性的，無法直接在血液裡自由流動。因此，在血管或淋巴管裡，脂質需要跟「載脂蛋白」這種特殊的蛋白質結合，變成可以親近水的「脂蛋白」，才能順利在全身循環運輸。

肝臟是生產這些「運輸用蛋白質」的主要工廠，製造出多種蛋白質來運載脂肪。其中，低密度脂蛋白載運大量膽固醇，將其精準送往各組織器官。這也是為什麼低密度脂蛋白膽固醇的縮寫是 LDL-C (全稱是 Low-Density Lipoprotein Cholesterol )。

當血液中 LDL-C 過高時，部分 LDL 可能會被「氧化」變質。這些變質或過量的 LDL 容易在血管壁上引發一連串發炎反應，最終形成粥狀硬化斑塊，導致血管阻塞。因此，LDL-C 被冠上「壞膽固醇」的稱號，因為它與心腦血管疾病的風險密切相關。

高密度脂蛋白（HDL） 則恰好相反。其組成近半為蛋白質，膽固醇比例較少，因此有許多「空位」可供載運。HDL-C 就像血管裡的「清道夫」，負責清除血管壁上多餘的膽固醇，並將其運回肝臟代謝處理。正因為如此，HDL-C 被視為「好膽固醇」。

過去數十年來，醫學界主流觀點認為 LDL-C 越低越好。許多降血脂藥物，如史他汀類（Statins）以及近年發展的 PCSK9 抑制劑，其主要目標皆是降低血液中的 LDL-C 濃度。

然而，科學家們在臨床上發現，儘管許多人的 LDL-C 數值控制得很好，甚至很低，卻仍舊發生中風或心肌梗塞！難道我們對膽固醇的認知，一開始就抓錯了重點？

傳統判讀失準？LDL-C 達標仍難逃心血管危機

早在 2009 年，美國心臟協會與加州大學洛杉磯分校（UCLA）進行了一項大型的回溯性研究。研究團隊分析了 2000 年至 2006 年間，全美超過 13 萬名心臟病住院患者的數據，並記錄了他們入院時的血脂數值。

結果發現，在那些沒有心血管疾病或糖尿病史的患者中，竟有高達 72.1% 的人，其入院時的 LDL-C 數值低於當時建議的 130 mg/dL「安全標準」！即使對於已有心臟病史的患者，也有半數人的 LDL-C 數值低於 100 mg/dL。

這項研究明確指出，依照當時的指引標準，絕大多數首次心臟病發作的患者，其 LDL-C 數值其實都在「可接受範圍」內。這意味著，單純依賴 LDL-C 數值，並無法有效預防心臟病發作。

科學家們為此感到相當棘手。傳統僅檢測 LDL-C 總量的方式，可能就像只計算路上有多少貨車，卻沒有注意到有些貨車的「駕駛行為」其實非常危險一樣，沒辦法完全揪出真正的問題根源！因此，科學家們決定進一步深入檢視這些「駕駛」，找出誰才是真正的麻煩製造者。

LDL 家族的「頭號戰犯」：L5 型低密度脂蛋白

為了精準揪出 LDL 裡，誰才是最危險的分子，科學家們投入大量心力。他們發現，LDL 這個「壞膽固醇」家族並非均質，其成員有大小、密度之分，甚至帶有不同的電荷，如同各式型號的貨車與脾性各異的「駕駛」。

早在 1979 年，已有科學家提出某些帶有較強「負電性」的 LDL 分子可能與動脈粥狀硬化有關。這些帶負電的 LDL 就像特別容易「黏」在血管壁上的頑固污漬。

台灣留美科學家陳珠璜教授、楊朝諭教授及其團隊在這方面取得突破性的貢獻。他們利用一種叫做「陰離子交換層析法」的精密技術，像是用一個特殊的「電荷篩子」，依照 LDL 粒子所帶負電荷的多寡，成功將 LDL 分離成 L1 到 L5 五個主要的亞群。其中 L1 帶負電荷最少，相對溫和；而 L5 則帶有最多負電荷，電負性最強，最容易在血管中暴衝的「路怒症駕駛」。

2003 年，陳教授團隊首次從心肌梗塞患者血液中，分離並確認了 L5 的存在。他們後續多年的研究進一步證實，在急性心肌梗塞或糖尿病等高風險族群的血液中，L5 的濃度會顯著升高。

L5 的蛋白質結構很不一樣，不僅天生帶有超強負電性，還可能與其他不同的蛋白質結合，或經過「醣基化」修飾，就像在自己外面額外裝上了一些醣類分子。這些特殊的結構和性質，使 L5 成為血管中的「頭號戰犯」。

當 L5 出現時，它並非僅僅路過，而是會直接「搞破壞」：首先，L5 會直接損傷內皮細胞，讓細胞凋亡，甚至讓血管壁的通透性增加，如同在血管壁上鑿洞。接著，L5 會刺激血管壁產生發炎反應。血管壁受傷、發炎後，血液中的免疫細胞便會前來「救災」。

然而，這些免疫細胞在吞噬過多包括 L5 在內的壞東西後，會堆積在血管壁上，逐漸形成硬化斑塊，使血管日益狹窄，這便是我們常聽到的「動脈粥狀硬化」。若這些不穩定的斑塊破裂，可能引發急性血栓，直接堵死血管！若發生在供應心臟血液的冠狀動脈，就會造成心肌梗塞；若發生在腦部血管，則會導致腦中風。

L5：心血管風險評估新指標

現在，我們已明確指出 L5 才是 LDL 家族中真正的「破壞之王」。因此，是時候調整我們對膽固醇數值的看法了。現在，除了關注 LDL-C 的「總量」，我們更應該留意血液中 L5 佔所有 LDL 的「百分比」，即 L5%。

陳珠璜教授也將這項 L5 檢測觀念，從世界知名的德州心臟中心帶回台灣，並創辦了美商德州博藝社科技（HEART）。HEART 在台灣研發出嶄新科技，並在美國、歐盟、英國、加拿大、台灣取得專利許可，日本也正在申請中，希望能讓更多台灣民眾受惠於這項更精準的檢測服務。

一般來說，如果您的 L5% 數值小於 2%，通常代表心血管風險較低。但若 L5% 大於 5%，您就屬於高風險族群，建議進一步進行影像學檢查。特別是當 L5% 大於 8% 時，務必提高警覺，這可能預示著心血管疾病即將發作，或已在悄悄進展中。

對於已有心肌梗塞或中風病史的患者，定期監測 L5% 更是評估疾病復發風險的重要指標。此外，糖尿病、高血壓、高血脂、代謝症候群，以及長期吸菸者，L5% 檢測也能提供額外且有價值的風險評估參考。

隨著醫療科技逐步邁向「精準醫療」的時代，無論是癌症還是心血管疾病的防治，都不再只是單純依賴傳統的身高、體重等指標，而是進一步透過更精密的生物標記，例如特定的蛋白質或代謝物，來更準確地捕捉疾病發生前的徵兆。

您是否曾檢測過 L5% 數值，或是對這項新興的健康指標感到好奇呢？

在奧運現代五項的馬術項目中，騎士必須隨機抽選馬匹作為搭檔，並在 20 分鐘的熟識時間後，上場跨越障礙。本屆的德國隊選手史勒（Annika Schleu）在馬術項目之前成績領先，但抽中的馬匹「聖男孩」（Saint Boy）不願配合跨越障礙，讓史勒情緒崩潰尖叫大哭，最終苦吞零分。

期間，場邊的教練蕾絲娜（Kim Raisner）往馬匹後腿捶了一拳，並要求史勒「真的打牠」，這樣的行為讓蕾絲娜在隔天被撤銷資格，也引發動物保護方面的議論。

賽事主辦方與媒體輿論，似乎都認為捶打馬匹是需要檢討的行為，然而矛盾的是，多數的賽馬比賽都允許鞭打馬匹，並宣稱能夠達到「鼓勵」馬匹、幫助馬匹轉向的作用，並確保比賽公平公正——以免騎士被質疑「故意放水」。

但以現今的觀點來看，利用鞭笞這類負向刺激來提升馬匹的表現，是近似體罰的概念，這樣的做法不但過時，而且相關研究也顯示，賽馬表現的好壞，與是否鞭打牠們完全無關^[1]！

鞭打有用嗎？兩種賽制比一比就知道

各大賽事皆規定了允許鞭打的次數與方式 ^[2] ，也有許多研究探討了騎士的用鞭技術與馬匹受傷的可能性，卻很少人懷疑過更根本的問題——鞭打對於馬匹的表現提升了多少？

若想要證明使用鞭子、馬匹轉向以及安全性之間的關係，那就必須讓同一批賽馬與騎士，在相同的場地與相近的時間裡，分別進行「無鞭打」與「可鞭打」的比賽，但賽馬可是一項十分昂貴的競賽，若要為了科學研究而舉辦多場比賽，那會燒掉多少研究經費呀！而且優秀的選手也不太會做多餘的出賽。幸好，英國已經同時在進行這兩種比賽了，並且在賽後都會由英國賽馬管理局（British Horseracing Authority BHA）發佈詳細的報告，內容記錄了與比賽有關的任何重要事項，這些素材正好可以拿來驗證「鞭打是否有用」！

於是，澳洲學者收集了 2017 年至 2019 年月之間的 126 份比賽報告 ^[3] ，其中包括 67 場無鞭打比賽（whipping-free，WF），與 59 場可鞭打的比賽（whipping-permitted，WP），並將條件相近的無鞭打比賽與可鞭打比賽匹配，再根據比賽報告的文字內容，以「賽馬的移動路徑偏移」、「賽馬間的相互干擾」、「騎師行為」等類目進一步比較，分析兩種賽制中，騎師鞭打馬匹與否對賽馬表現的差異。

基於「鞭打有正向作用」的假設，可鞭打賽事的組別應該要有更好表現，也就是賽馬移動路徑偏移較少、 賽馬間的相互干擾較少，馬匹與騎士的異常行為紀錄也應該較少，並且完賽所花費的時間應該要更短。

結論：無鞭打比賽更接近「純粹的競速」

根據研究分析指出，共有 67 場比賽紀錄到馬匹有移動路徑偏移的狀況，根據偏移方向又可細分為 2 組：「向左偏移」總共發生了 34 次，其中 19 次發生在可鞭打組，多過發生在無鞭打組的 15 次；「向右偏移」總共發生了 33 次，17 次發生在可鞭打組， 多過發生在無鞭打組的 16 次——換言之，允許鞭打組發生了更多次偏移！這樣的結果顯示，鞭打並未減少馬匹在賽場上的軌跡偏移，當然也無助證實「鞭打可以幫助馬匹轉向」的說法。

至於「賽馬間的相互干擾」，具體上包含碰撞、阻擋、踩腳後跟等行為，在比賽中可能引發嚴重的意外！而且相信無論持鞭與否，沒有騎士樂見自己駕駛的賽馬變成碰碰車（？）。但研究卻指出，在可鞭打的比賽中，賽馬間的干擾發生了 37 次 （占 61%），多過無鞭打比賽中發生的 24 次（占 39%）。其中「未明確定義的干擾」更是 16：9 的懸殊比例，看來「持鞭可以幫助人馬合一，因此更能保障賽事安全性」的說法也是不攻自破。

另外，騎師的異常行為總共被記錄到 21 次，可鞭打比賽占了其中 9 個，無鞭打比賽占 12 個，然而根據報告紀載，其中過半數是騎士個人的粗心或失誤行為，例如騎士鬆開了韁繩，這與是否鞭打的關係較不明顯。

而最重要的證據 —— 兩種賽制的完賽時間差異，一般來說會假定被鞭打的馬匹跑得比較快，但「可鞭打比賽」的完賽時間有更短嗎？結果是沒有！其與「無鞭打比賽」的完賽時間沒有顯著差異，兩者幾乎相差無幾，兩種賽制標準誤差僅 0.351 秒。

總而言之，騎師的鞭打行為，對於賽馬的競賽表現、賽馬的轉向、減少賽馬間的干擾都沒有幫助，無鞭打比賽也證實了不影響比賽的公正性及完整性， 該是時候開發更科學有效又人道的訓馬方式了！

人馬羈絆數千年，不如追尋更有愛的可能

在《斯卡羅》劇中，飾演李仙得的法比歐對馬背上的蝶妹說：「馬會察覺你的所有感受，你相信牠，牠就會相信你。」這可不只是愛馬人士的自作多情，2016 年發表在《生物學快報》上的研究^[4]，首次證明了馬兒真的能讀懂人類臉上的表情。

研究人員發現，若給馬兒看表情憤怒的人類照片，他們的心跳會加快，並開始表現出與壓力有關的行為；奇妙的是，如果馬兒看到的是表情快樂的人類照片，馬匹的生理變化並不明顯，雖然我們無法知道馬兒的真實想法，但這或許跟動物識別威脅的天性有關。

鞭子在馬兒眼中應該是個威脅吧？或許我們能減少使用鞭子，與馬兒建立更緊密的夥伴關係，讓馬兒擁有更健康的心理狀態，那才更接近「完整的比賽」。

1. Mackinnon, M.; Johnson, P. The case against productive whipping. Explor. Econ. Hist. 1984, 21, 218.
2. Jones, B.; Goodfellow, J.; Yeates, J.; McGreevy, P.D. A critical analysis of the British Horseracing Authority’s review of the use of the whip in horseracing. Animals 2015, 5, 138–150.
3. Thompson, K.; McManus, P.; Stansall, D.; Wilson, B.; J.; McGreevy, P.D. Is whip use important to thoroughbred racing integrity? What stewards’ reports reveal about fairness to punters, jockeys and horses. Animals 2020, 10, 1985.
4. Smith, AV.; Proops, L.; Grounds, K.; Wathan, J.; McComb, K.. Functionally relevant responses to human facial expressions of emotion in the domestic horse (Equus caballus). Biol Lett. 2016, 12:20150907. 

「孤雌」生殖，但是永遠需要精子

如今常用的模式生物：秀麗隱桿線蟲（Caenorhabditis elegans），最早慧眼識線蟲的是法國生物學家 Victor Nigon。在 1949 年時，他還記錄了一種土壤中的線蟲 Mesorhabditis belari，這種線蟲只有少量男生，男生會和女生交配，卻很少將 DNA 遺傳給後代。

而最近的新研究也發現，這種線蟲的生殖方式真的十分特殊，且相當巧妙。[1][2]

Mesorhabditis belari 線蟲是本文的主角，之後直接簡稱作「線蟲」。它的生殖方式算是孤雌生殖（parthenogenesis），卻又不是典型的孤雌生殖。孤雌生殖屬於無性生殖的一種，往往不需要男生，只要有媽媽就能生下女兒，例如大理石紋螯蝦。

某些孤雌生殖的動物卻需要精子刺激，才能讓卵母細胞活化，發育為胚胎。

此一孤雌生殖的方式稱作「假受精（pseudogamy）」、「雌核發育（gynogenesis）」，或是「依賴精子的孤雌生殖（sperm-dependent parthenogenesis）」，通常用的是別種動物的精子，而這些精子只作為啓動器使用，精子本身的 DNA 不會影響胚胎的遺傳組成。

但線蟲又不太一樣，她們是利用同種男生的精子激活卵子，然而儘管使用同類的精子，男生的遺傳物質同樣無法傳承下去。

有上過演化課的話，應該會感到非常可疑。世界上不同生物的生殖方式無奇不有，但是再獵奇也不該與演化原則衝突：不同性別間的利益要達到平衡，否則將系統崩潰，導致生物滅絕。

假如像線蟲這樣，女生缺乏男生就無法受孕，但是男生付出代價後，卻也無法傳承自己的遺傳物質作為回報，對男生沒有好處；這種看似依賴單方面奉獻的生殖系統，是如何維持的呢？

無性生殖、有性生殖，同時進行

線蟲在實驗室環境下，一輩子產下的後代總是約有 9% 男生。線蟲女生一定要有同種男生的精子，才能產下後代，而男生也無法跨物種情慾交流，因此，男生在生殖中的功能，只有讓同種女生受孕。這是為什麼呢？線蟲的卵細胞發育為胚胎，為什麼非要精子不可？

細胞發育與分裂的時候，需要形成正確的結構拉開空間。 線蟲受精以後，精子可以提供細胞骨架的材料，作為中心體（centrosomes）讓胚胎能夠正常分裂。這些結構卵細胞無法自行生產，必需要靠精子提供，胚胎才能正常發育。

線蟲女生會製造兩種胚胎，實驗總共觀察的 258 個胚胎中，大部分 227 個是雌核發育（gynogenetic），小部分 31 個是兩性融合（amphimictic）。兩種胚胎形成的性別截然不同，雌核發育胚胎都長成女生，兩性融合胚胎皆發育為男生。

如此生下的後代，源自雌核發育的女兒，完全不會繼承任何精子的 DNA，遺傳上 100% 複製母體，可以算是無性生殖的產物。源於兩性融合的兒子，則是繼承精卵各一半的遺傳物質，能視為有性生殖的個體。

為什麼兩性融合的胚胎，幾乎全部發育為男生？這是由於精子不同所致。線蟲與人類一樣，都用 X、Y 性染色體決定性別。不論雌核發育或是兩性融合胚胎，配備 Y 染色體的精子穿透機率都高達 90%，遠遠超過配備 X 的精子。

然而，雌核發育的胚胎不會傳承男生的遺傳物質，獲得哪種精子沒有差別；兩性融合的胚胎則是有很高比例得到 Y 精子，假如接收到 X 往往還會陣亡。

這些因素綜合起來，最終的結果是：高比例的雌核發育胚胎全部形成女兒，低比例的兩性融合胚胎通通產生兒子，大約占 9% 左右。

為什麼總是生9%兒子？

了解線蟲怎麼生寶寶以後，接著要回答的問題是：為什麼兒子總是 9%？後代的性別比例，其實可以歸納為數學問題。研究者使用「賽局」模型，希望參透線蟲的生殖天機。生女生男的賽局中，有哪些條件要考慮呢？

以線蟲女生角度來看，受孕需要精子，所以沒有男生不行；但是男生只有卵細胞啓動器的功能，不能傳承 DNA，生太多兒子又是浪費資源；更重要的是，假如兒子去當別的媽媽的卵細胞啓動器，對自己的世系將毫無幫助。

綜合起來就是：

媽媽一定要生兒子，但是比例不需要太高，能精子不落外人田更好。

為了妹妹，甘心成為生殖後代的零件吧

對線蟲男生而言，自己的整個基因組，都無法傳承給有生殖能力的後代，這樣活著還有什麼意義？

且慢！有聽過這句話嗎？

「我將會為兩位兄弟或是八位表親犧牲生命。（I would lay down my life for two brothers or eight cousins）」

這句名言來自族群遺傳學界的上古神獸霍爾丹（J.B.S. Haldane），他的意思是，血緣關係更親近的個體，之間共享更多遺傳成分，從演化來看，「一個我」量化以後等於「兩位兄弟」或「八位表親」。此一概念，後來成為解釋利他行為（altruism），與重要理論親擇（kin selection）的基礎。

身為線蟲男生，儘管註定沒有後代，卻會有大概 10 位姐妹（由於許多男生出生的比女生早，他們將擁有很多妹妹）。他們與姐妹間，有部分遺傳組成是共通的，如果能協助自己的姐妹生寶寶，等於能間接傳播自己的 DNA，又有利於自己所屬的世系。

由上述假設的條件推論，如果地方的媽媽生下一定比例的兒子，兒子又大部分留在附近，傾向和自己的同母姐妹情慾交流，就可以達到兩性都能接受的平衡。而賽局模型估計，要達到此一平衡的男生比例是：9%。

生物個體的細胞，可以分為生殖細胞與體細胞兩種。線蟲男生雖然也是獨立的個體，不過以生殖狀態來看，卻可以視為供應中心體的「體細胞」。這似乎有點像是蜜蜂，不過又不一樣。

大自然的賽局平衡

孤雌生殖是演化的結果，並不會總是維持現狀。孤雌生殖的動物，可以完全不需要男生，也可能無法長期維持無性生殖，又回到有性生殖或是不幸滅團。

經過一系列精巧的研究以後，研究團隊終於釐清 Mesorhabditis belari 線蟲繁衍後代時，同時綜合無性與有性生殖的細胞機制；也以賽局計算，得知兒子的比例為什麼總是 9% 的原因。

線蟲的生殖機制，不論當初是如何形成，都使得它當下處於微妙的平衡上，保持在「自體假受精（autopseudogamy）」的特殊狀態。

延伸閱讀

• 三倍體複製蝦全面入侵——進擊の大理石紋螯蝦（上）
• 缺乏遺傳多樣性的孤雌生殖，註定死路一條？——進擊の大理石紋螯蝦（下）
• 蟻生online上線：如何決定成為要生寶寶或是做工的螞蟻？
• 偵探故事般的關鍵兇手：自私基因
• 《跟孫臏比一場賽馬吧！》——2018數感盃 / 高中組專題報導類第二名
• 比傳說對決更精彩！線蟲與真菌的生死之戰

• 1. Grosmaire, M., Launay, C., Siegwald, M., Brugière, T., Estrada-Virrueta, L., Berger, D., … & Félix, M. A. (2019). Males as somatic investment in a parthenogenetic nematode. Science, 363(6432), 1210-1213.
  2. In this nematode species males are needed for reproduction but not their genes

本文亦刊載於作者部落格《盲眼的尼安德塔石匠》暨其 facebook 同名專頁。

「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後，一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習，運用數學知識，培養及展現邏輯思考與文字撰寫的能力，盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。

本文為 2018數感盃青少年寫作競賽 / 高中組專題報導類佳作 之作品，為盡量完整呈現學生之作品樣貌，本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

• 作者：謝亞彤、林芳緯／竹科實中

「賽局」這個名詞已頻繁的出現在我們生活中，學者們將人類的互動科學化後，成為了有趣的賽局理論，廣泛的運用在日常生活中。但早在 1944 年數學家馮·諾伊曼與奧斯卡·摩根斯特恩合作著述《賽局理論與經濟行為》前，西元前四世紀的中國，著名的軍事家孫臏就已運用賽局理論讓自己在紛亂的戰國時期嶄露頭角了！

話說可憐的孫臏被同窗龐涓陷害，龐涓仗著自己是魏國大將軍砍斷了孫臏的雙腳又在他臉上刺字，如此侮辱人又不乾脆的痛下殺手，日後對方必定會加倍奉還的。果然天無絕人之路，一日齊國使者出使魏國首都大梁，孫臏以刑徒的身分秘密拜見使者，以自己三寸不爛之舌的功力讓使者偷偷把自己運回齊國，並得到齊國將軍田忌的賞識，待孫臏如上賓。不久《史記孫子吳起列傳》中所記載家喻戶曉的「田忌賽馬」正式展開：

忌數與齊諸公子馳逐重射。孫子見其馬足不甚相遠，馬有上、中、下輩。

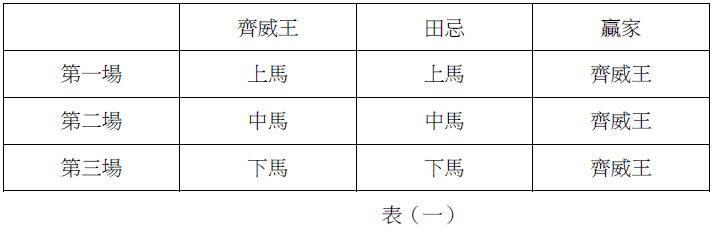
齊國的大將軍田忌很喜歡賽馬，並時常與齊國眾多公子賽馬。有一次，他決定挑戰齊威王的馬匹。他們商量好，將各自的馬分成上，中，下三等。比賽的時候，雙方以上馬對上馬，中馬對中馬，下馬對下馬。

在這裡我們不用任何公式就能百分之百證明田忌會輸，齊威王與諸公子每一個等級的馬都要比田忌的還強，因為他們是貴族諸侯，區區一個將軍如何與他們匹敵？（當然，如果兩方實力不分軒輊也不用賽馬了，田忌大概早因功高震主被做掉了。）

如表（一）所示，田忌不出讀者所料的屢戰屢敗。正當他覺得掃興時，他的幕僚孫臏向他走來（等等，他的腳不是斷了嗎？）。孫臏在經過前一場比賽的觀察後胸有成竹的向田忌打包票：「大人您儘管下注，臣必讓您取得最終的勝利！」

田忌縱使疑惑但為了面子為了錢依舊加碼他的賭金，而齊威王屢戰屢勝，正在興頭，看到田忌不服輸的舉動，也霸氣的命令部下把前幾次贏得的銀錢全部抬來，還額外押了一千兩黃金。齊威王輕蔑地說：「那就開始吧！」一聲鑼響，比賽開始了！

孫子曰：「今以君之下駟與彼上駟，取君上駟與彼中駟，取君中駟與彼下駟。」既馳三輩畢，而田忌一不勝而再勝，卒得王千金。

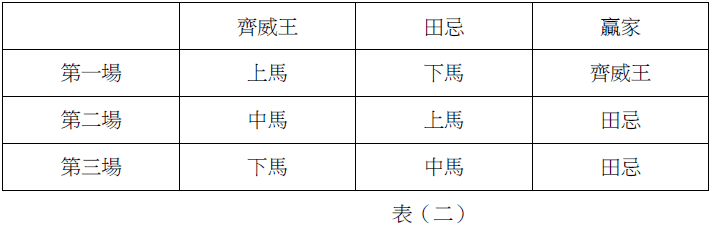
鑼聲鏜鏜響，田忌的心蹦蹦跳。第一局孫臏先以下等馬對齊威王的上等馬，結果田忌又輸了。齊威王站起來嘲諷的說：「經過前幾次的慘敗，將軍你還學不到教訓嗎？」田忌沒有答應。（實在不是因為要故作姿態，而是他的心現在正為了賠輸的錢淌血阿！）接著進行的第二場比賽，孫臏拿上馬對齊威王的中馬，終於獲勝了一局，這時齊威王開始面露緊張了。最後一局比賽，孫臏拿中馬對齊威王的下馬，又戰勝了一局。這下，齊威王簡直不可置信，田忌竟然以同樣的馬匹，三戰兩勝贏了齊威王！如表（二）所示，比賽結果大挫齊威王的傲氣。

田忌與齊威王的賽馬屬於賽局論（Game Theory）中的非合作賽局（Non-cooperative Game），即人們在利益相互影響的局勢中會如何制定策略使自己的收益最大。在表格中，賭金轉換成一分，因為在嚴格公平的競爭下，一方的損失也就是對方的得利，這種賽局往往是有輸有贏拚得你死我活，所以雙方玩家不可能存在合作的可能，而他們的收益與損失的總和永遠為「零」。

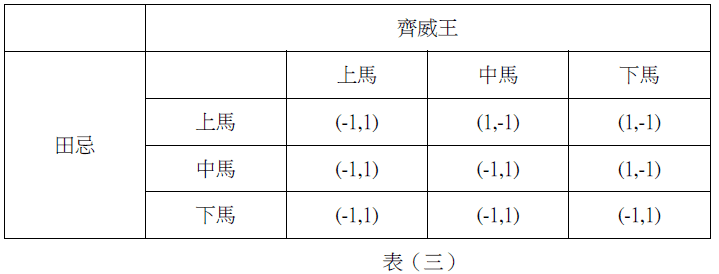
因此我們將孫臏幫助田忌的比賽結果轉換為下表（三）：

表格中的（x，y），x表示田忌的勝負，y表示齊威王的勝負。-1 與 1 則分別代表敗與勝的報酬。田忌獲勝的情形有三種，分別是上對中、上對下、中對下，但同一局（三場）比賽中不能派出兩次上馬，因此本賽局對田忌的最佳策略，就為下對上、上對中、中對下。

孫臏能選擇正確的出賽馬匹順序為 1/3×1/2×1/1=1/6 但又因為齊威王是按原先規定以上中下的次序派馬匹，因此獲勝機率就變成1了。（所以故事中田忌能輕鬆取勝，都要歸功於齊威王是遵守規定的乖寶寶真君子！？）

這場賽馬又可稱為靜態賽局（Static Game），也就是齊威王與田忌同時採取行動，或者說，雖然不同時但後行動的人不能改變原有的出場順序，即使知道對方的出場序也不能改變自己的。）

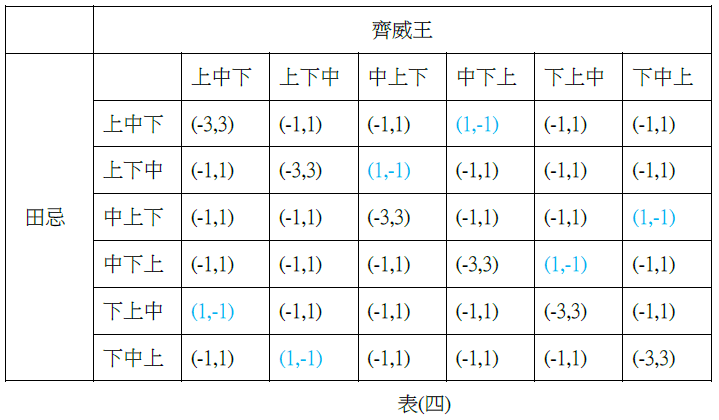
假如今天除了孫臏知己知彼，而齊威王也知道田忌的幕僚中有孫臏這麼厲害的角色，那齊威王也可以與孫臏一樣顛覆規則，摒棄原本上中下的出場次序。這種賽局即稱為動態賽局（Dynamic Game），也就是兩人都能在對方行動後立即應變。如表（四）所示。（1，-1）、（-1，1）的含意與表（三）相同，而（-3，3）為田忌三場連敗之意。

在更複雜的完全訊息動態賽局中，田忌的勝率為 6/36=1/6

如果有一天，齊威王與田忌雙雙來到現代，上演一場跨時代的穿越戀愛劇（喂！你們拿錯劇本了！）進行一場 Bromance 的賽馬，按照現今盛行賽馬的香港賽馬會規則，馬匹分成五等，意思是要比五場。假設五場出賽馬匹次序如故事一樣能隨意替換，那田忌獲勝的機率會是多少？

首先依據馬匹由強到弱以 1~5 表示，若號碼相同則齊威王勝，會有 5！× 5！=14400 種的出賽馬匹組合順序。若已知齊威王派出順序為（1，2，3，4，5）的馬匹出賽，則田忌可派出（1，5，2，3，4）、（2，1，5，3，4）……等 27 組順序的馬匹出賽以贏得勝利。依此推類，在 14400 種馬匹出賽組合中，田忌總共有 27×5！=3240 種組合可贏得勝利，勝率為 3240/14400=9/40

對孫臏來說，算出的勝率 9/40 大於原先賽三匹馬的 1/6，我們或許可以預測如果孫臏穿越時空來到現代，他也會是賽馬場的常勝軍！

時序來到三國時期，天下奇才諸葛丞相也有與孫臏同樣的見解（真是英雄所見略同），還特別指出孫臏的賽馬說實為兵說也。

諸葛亮在《權書·強弱》中接著說：「下下之不足以與其上也，吾既知之矣，吾既棄之矣。中之不足以與吾上，下之不足以與吾中，吾不既再勝矣乎？」諸葛亮深諳權衡之計，唯有放棄小利，才能保全大局，贏得最終的勝利。「得之多於棄也，吾斯從之矣。彼其上之有三權也，三權也者，以一權而致三者也。」所以藉著這一場賽馬，孫臏要告訴齊威王的不只是單純的賽馬而已，更是領軍致勝之道，齊威王能領略這種高深的寓意也不是泛泛之輩，齊國而後能稱王於中原，自齊威王始也。

這場歷史性的賽馬，大概是孫臏最為人津津樂道的趣事了（人們總是喜歡看弱勢的一方運用謀略反敗為勝阿！），不僅讓他能獲得重用，其後他也才得以名顯天下，世傳其兵法，成為中國軍事史上耀眼的星子。（也讓現今莘莘學子得到一個研究題材）

在現實生活中，我們也能藉著跳脫慣性思維，嘗試考慮對方各種可能的行動方案，並選擇對自己最有利或最合理的策略（廢話，沒有人喜歡虧損，但正因為沒有人不會虧損，所以更加凸顯賽局分析的重要性），如此下回賭博時我們也能親自實踐孫臏的機智贏得更多錢！

參考資料：

• https://kknews.cc/zh-tw/news/3m9vjzg.html 每日頭條田忌賽馬與動態推理
• http://wiki.mbalib.com/zhtw/%E9%9B%B6%E5%92%8C%E8%B5%9B%E5%B1%80 MBA智庫零和博弈
• https://talkecon.com/sawgame1-5/ 白經濟 賽局奪魂鋸 1.5
• http://boktakhk4.pixnet.net/blog/category/1456108 田忌賽馬@故事欣賞

更多2018數感盃青少年寫作競賽內容，歡迎參考 2018數感盃特輯、數感實驗室官網及粉絲頁喔。