統計數據是天大的謊言?我們該如何理解統計結果——《塗鴉學數學》
作者/ 班‧歐林 (Ben Orlin);譯者/王年愷
好,我們先把這件事情說清楚。統計數據是謊言,不應該採信。史上最聰明的人都這樣說過,不是嗎?
圖/臉譜出版提供
我的重點是什麼?沒錯,數字會欺騙。但文字也會——更不用說圖案、手勢、嘻哈音樂劇和募款電子郵件了。我們的道德制度會去責怪說謊的人,而不是說謊者用來說謊的媒介。
對我來說,最有意思的批評統計之詞不是批評統計學者的不誠實,而是批評數學本身。我們可以去理解統計的瑕疵,看到每一項統計數據想要捕捉什麼(以及它會刻意忽略什麼),來增強統計的價值。也許這樣我們就能成為威爾斯想像中的優良公民。
統計中的平均數(mean)其實分配不均?
圖/臉譜出版提供
圖/臉譜出版提供
做法 :把你的資料全部加起來,把總數除以資料筆數。
使用時機 :平均數滿足了統計的一項基本需求:捕捉一個群體裡的「中間傾向」。籃球隊的身高是多少?你每天賣出幾個冰淇淋甜筒?這班學生的考試成績如何?如果你想用一個數值來概述一整個群體,平均數是合理的第一步。
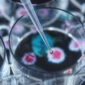
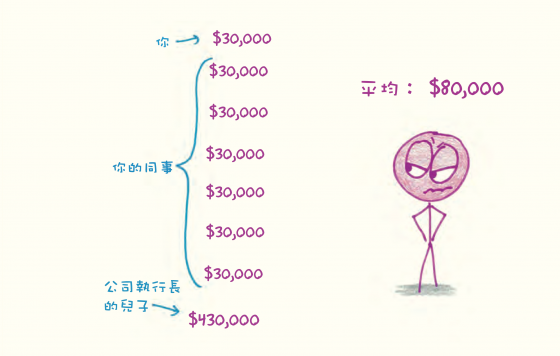
為什麼不要相信它 :平均數只管兩個資訊:總和,以及用來達成這個總和的人數。假如你曾經分配過海盜搶來的財寶,就知道哪裡危險了:分配的方式有許多種。每一個人分別貢獻了多少?這是否平均,還是嚴重偏袒某一方?
如果我吃掉一整個披薩,沒有留下任何一點給你,我們是否可以公正地說每個人「平均吃掉」半個披薩?你可以跟你邀來吃晚餐的客人說,「人類平均」有一顆卵巢和一顆睪丸,但這樣是不是會讓氣氛突然冷掉?(我試過;的確會。)
人類關心分配的問題,但平均數會忽略這個問題不談。
圖/臉譜出版提供
但平均數還有一個有用之處:它的特性使得它容易計算出來。
假設你的考試成績是 87 分、88 分和 96 分。(對,你在這班如魚得水。)你的平均是多少?你不必耗費腦力去加減乘除,只需要重新分配就好了。
從你最後一次的成績拿走 6 分,把 3 分分給第一次、2 分分給第二次。這樣你的分數便是 90 分、90 分和 90 分,另外還多了 1 分。把這 1 分分配給三次考試,你就會得到平均為 90⅓,完全不需要多花腦力。
統計中的中位數(median)忽視懸殊差異?
圖/臉譜出版提供
圖/臉譜出版提供
做法 :中位數是你的資料集裡最中間的那一筆。有一半的資料比它低,另一半比它高。
使用時機 :中位數和平均數一樣,捕捉了一個群體裡的中間傾向。差別在於它對離群值(outlier)的敏感度—或者應該說,它有多麼不敏感。
就拿家庭所得來說吧。美國的富裕家庭可能收入是貧窮家庭的幾十倍(甚至幾百倍)。平均數假裝讓每一個家庭都分配到收入總和的同樣數量,因此它會被這些離群值吸引走,離開大多數資料群聚的地方。這樣它算出的數值是 $75,000。
中位數抗拒離群值的吸引力。它指認出絕對位於美國正中間的家庭所得,這會是剛剛好的中間點,有一半的家庭比這富裕,另一半比這貧窮。在美國,這個數值接近 $58,000。
它和平均數不一樣;中位數可以讓人清楚看到「典型的」家庭是什麼樣子。
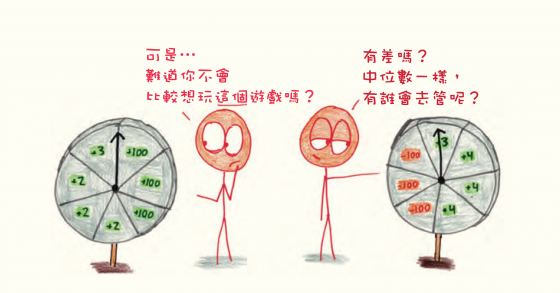
為什麼不要相信它 :當你找到中位數後,你知道有一半的資料比它大,另一半比它小。但這些數值距離它多遠—只有半步之遙,還是要橫越整片大陸?你只會看到中間的那一塊,不會去管其他部分有多大或多小。這樣你可能誤判。
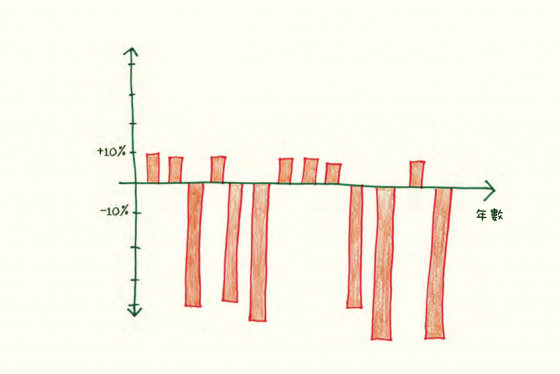
圖/臉譜出版提供
當一位創業資本家投資新創公司時,他會預期大多數新創公司將失敗。十分之一的罕見成功案例彌補其他小小的損失。但中位數會忽略這樣的動態。它大叫:「通常的結果是負面的。快中止任務!」
同理,保險公司細心建立一套組合,因為他們知道千分之一的罕見災難會消滅多年以來不太高的獲利。但中位數忽略潛在的大災難。它鼓舞你:「通常的結果是正面的。永遠不要停下來!」
這就是為什麼你常常看到中位數與平均數並列。中位數報出通常的數值,平均數則是報出總數。它們像是兩位有缺陷的證人,兩個合起來的時候會說出比任何一個更全面的故事。
統計中的眾數(mode)排除與眾不同?
圖/臉譜出版提供
圖/臉譜出版提供
做法 :它是最常見的數值,最潮、最時尚的資料點。假如每個數值都獨一無二、沒有重複呢?這樣的話,你可以把資料分類,然後把最常見到的那個類別稱為「眾數組」(modal category 或 modal class)。
使用時機 :眾數在進行民意調查和統計非數字的資料時非常出色。假如你想要簡述大家最喜歡的顏色,不可能「計算出顏色的總和」來算出平均數。或者,假如你在舉行投票,如果把所有的選票從「最自由派」排到「最保守派」,然後把公職給拿到中位數選票的候選人,這樣會讓選民發瘋。
為什麼不要相信它 :中位數會忽略總和。平均數忽略總和的分布。那眾數呢?它會忽略總和、總和的分布和幾乎所有其他的事情。
眾數只代表單一個最常見的數值。但「常見」的意思不是「有代表性」。美國的薪資眾數是 0——這不是因為大多數美國人破產又沒工作,而是有領薪水的人分布在 $1 到 $100,000,000 的光譜各處,但所有沒領薪水的人都有相同的數字。這項數據不會告訴我們任何和美國有關的事。這項事實幾乎在所有國家都適用,因為這是金錢的運作方式所造成的。
改用「眾數組」只能解決一部分的問題。這樣會讓呈現資料的人有驚人的權力,因為他可以故意操弄分組的界線,來配合他的立場。依照我劃分界線的差異,我可以宣稱美國家庭所得的眾數位在 $10,000 到 $20,000(以 10,000 進位),或 $20,000 到 $40,000(以 20,000 進位),或 $38,000 到 $92,000(以所得稅級距進位)。
同樣的資料集,同樣的統計數據,但最後的樣貌完全改變了,端視畫出這個樣貌的畫家採用哪一種畫框而定。
塗鴉學數學:以三角形打造城市、用骰子來理解經濟危機、玩井字遊戲學策略思考,24堂建構邏輯思維、貫通幾何學、破解機率陷阱、弄懂統計奧妙的數學課 》,2020 年 5 月,臉譜出版

































 ——本文摘自《
——本文摘自《