載入中 ...
人與人之間的競爭與合作是很難拿捏的事。很多時候，雙方合作比不合作能給各自帶來更大的好處，但是一廂情願地合作的人，卻有可能被對方視為「潘仔」或「傻瓜」（Sucker）而予取予奪。於是，在各自的利害考量下，沒有人願意合作，寧可兩輸也不願意當「潘仔」。這種困境，可以存在於人際關係，經濟交易，政治角力，國際關係，甚至自然環境的維護，在人生及社會上，可說屢見不鮮。
英國BBC電視中心製作的Golden Balls便是模擬這種困境的競賽節目。節目中，二參賽者爭取一筆獎金，例如1000英鎊。二人隔桌對坐，面前各有兩顆金球，其中一個金球裡面寫著Split（平分），另一個寫著Steal（竊佔）。如果二人均選擇Split，則獎金平分。如果二人均Steal，則獎金槓龜。而如果一人Steal而另一人Split，則Steal者獨佔全額獎金，而Split者只能抱蛋含恨而歸。此賽局可用下圖來表示：
| Player B | |||
| Split | Steal | ||
| Player A | Split | 500, 500 | S, 1000 |
| Steal | 1000, S | 0, 0 | |
其中S雖然表面上也是0，其實比零還糟，因為若雙方均Steal，雖然無人得獎，畢竟互相扯平，而單方面的Split除了抱蛋而歸外，還要加上當「潘仔」的懊惱、義憤、和羞辱，所以S<0。（讀者可以自問：你寧可Steal而雙輸呢，還是Split而當「潘仔」？）如此，則理性的參賽者會算計：如果對方Split，自己的較佳策略是Steal，因為Steal會贏得全額獎金，而Split則只能贏得一半。而如果對方Steal，則自己更應該Steal，否則就要當大傻瓜了。於是，對理性的參賽者而言，Steal是一個「優勝策略」。而如果雙方均如此算計，結果就獎金就槓龜了。
「金球」節目容許參賽者在決定之前互相溝通，可是即使雙方協議Split，因為口說無憑，輕易信賴對方的承諾反而容易吃虧上當。以下這場獎金高達100,000英鎊的金球大賽即紀錄了輕信人言的苦果：
Golden Balls 所顯示的困境，正是所謂的「囚徒困局」 （Prisoner’s Dilemma）。囚徒困局是賽局理論中一種非零和賽局，它反映了人際間常見的困境。這個賽局可以表現如下：
| Player B | |||
| C | D | ||
| Player A | C | RA, RB | SA, TB |
| D | TA, SB | PA, PB | |
定義：
A,B：參賽者
C,D：策略。C=合作（Cooperate），D=不合作或背叛（Defect）
TA,RA,PA,SA：參賽者A在表中各種策略組合下的收益
TB,RB,PB,SB：參賽者B在表中各種策略組合下的收益
T=Temptation，R=Reward，P=Punishment，S=Sucker’s Payoff
賽局的假設：
- A,B均只為自己利益著想
- A,B無法達成彼此信賴的有效承諾
- TA>RA>PA>SA
- TB>RB>PB>SB
賽局中，A,B二人均可以自由選擇合作或不合作兩種策略。在上列假設下，A,B均會發現不論對方合作或不合作，不合作比合作會給自己帶來較大的收益：假使對方合作，你合作可以得到收益R，而不合作則能得到收益T>R；假使對方不合作，你合作可以得到收益S，而不合作則能得到收益P>S。這樣算計的話，二人均不會合作，結果獲得P的收益。然而，二人旋即發現如果二人均合作的話，收益R比P要來得好（R>P）。可是在無法信賴對方的情況下，自己片面合作是不智的，因為對方如果還是不合作的話，對方將會得到最好的收益T，而自己將會得到最壞的收益S。於是，二人會陷於相互背叛的困境。
賽局理論中，D是所謂優勝策略（dominant strategy），也就是不論對方選擇何種策略，選擇D均會給自己帶來較大的收益。相互背叛的（D,D）策略組合是所謂的納許均衡（Nash equilibrium），也就是在（D,D）的情況下，沒有人會片面改採其它策略。可是（D,D）不是所謂的伯瑞多最佳結果（Pareto optimal outcome），因為（C,C）帶來的收益，對兩人均要比（D,D）帶來的收益要來得好。這個賽局之為困局正是因為它唯一的Nash equilibrium不是Pareto optimal。它之所以稱作囚徒困局，是因為以下的故事：
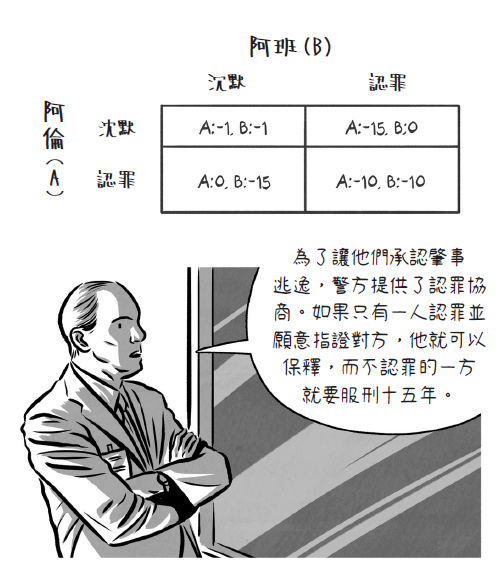
二人共同犯罪被捕而成為囚徒。檢察官要囚徒認罪，但告知他們其求刑不僅與個別囚徒認罪與否有關，也與共犯認罪與否有關：如果二人均供認犯行不諱，則證據確鑿，檢察官將求刑3年。如果二人均不認罪，因證據不足，檢察官將只能以技術性的微罪求刑1年。如果一人認罪而另一人不認罪，則檢察官會對認罪之人處分不起訴，而對不認罪之人求處重刑5年。如果把不認罪視為二囚徒之間的合作而認罪視為相互背叛，則這個故事符合如下的賽局：
| Player B | |||
| 不認罪 | 認罪 | ||
| Player A | 不認罪 | -1, -1 | -5, 0 |
| 認罪 | 0, -5 | -3, -3 | |
因為TA=TB=0，RA=RB=-1，PA=PB=-3，SA=SB=-5，T>R>P>S對A，B二人而言均成立，所以認罪（D）是dominant strategy。二人均會認罪（D,D）。二人於是會被檢察官求刑3年。（D,D）是為Nash equilibrium。可是（D,D）不是Pareto optimal，因為（C,C）只會被求刑1年。雖然如此，二人在無法相互信賴的情況下還是會互相背叛而認罪。這是囚徒困局的原型典故。上面Golden Balls的賽局中，TA=TB=1000，RA=RB=500，PA=PB=0，SA=SB<0，也是T>R>P>S 對A，B二人而言均成立，因此它是不折不扣的囚徒困局。
Golden Balls賽局容許參賽者在決定Split或Steal之前互相溝通，這是賽局理論所謂的「訊號傳送」（signaling）機制，讓參賽者向對方暗示甚或明示自己是何種類型的玩家。賽局理論一般認為參賽者要付出相當的代價才能讓他傳送的訊號具有可信度，而廉價的訊號只是舌燦蓮花（cheap talk）而已。例如參賽者可能發誓一定會合作，但發誓伴以「斬指頭」的代價顯然要高於「斬雞頭」的代價，前者所傳送的訊號會比後者要可信得多。Golden Balls的參賽者即使信誓旦旦會Split，沒有「斬指頭」之類的行為保證，終究是舌燦蓮花，不足深信。
那麼為何有些Golden Balls參賽者願意Split？賽局理論純粹是數學理論，在實證上並沒有百分之百的預測能力。「理性」有其經驗上的分配：不同國家、文化、宗教、社會、種族、性別、收入、教育等等的人參與Golden Balls都可能做出不同的選擇。而且Golden Balls的signaling雖然是cheap talk，不同的人也可能有不同的反應，例如有些人就容易相信態度誠懇或英俊漂亮的參賽者所傳送的訊號。「理性」終究只是理論上的假設，它是否客觀事實仍有待經驗檢定。
原刊載於Tse-min Lin 的部落格
PanSci TALK重出江湖啦！4/27（六） 在讀者與作者之間：譯者的視界 講座，我們邀請兩位經驗豐富的科普書作者與譯者。首先由楊玉齡女士分享【科普書的修煉】，第二階段則由林俊宏先生分享【翻譯書的奇幻之旅：從作者、版權、譯者、編輯到讀者】。對於科普書寫作、翻譯、製作有興趣的朋友們不容錯過！
- 參與活動就有機會獲得《人類大歷史》、《人類大命運》、《21世紀的21堂課》、《肝炎聖戰》、《意識之川流》、《植物彌賽亞》等好書喔！
- 由此去報名
