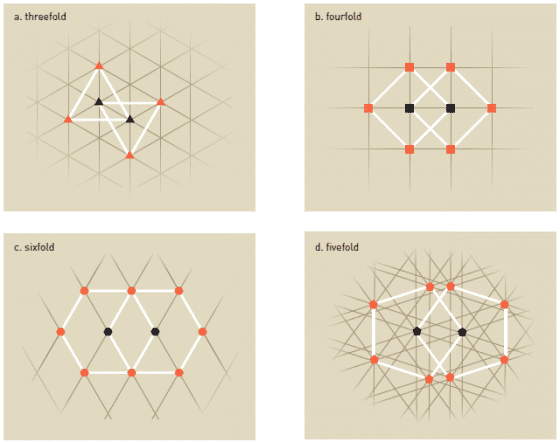
這幾年,越來越多人到日本旅行了。
旅行有所謂的「定番景點」,例如京都金閣寺或清水寺。旅客或者以朝聖的心前往,或者抱持著總得來一下的交報告心態,與金閣寺合影存證。通常,後者比較喜歡私房景點,少了遊覽車與觀光客的喧囂,鏡頭裡沒有十萬個後腦杓,彷彿潛到深水似地,更融入當地的生活。
既然都出國旅行了,當然想體驗些特別的,飛到幾千公里以外的地方,還是去個好像巷口頂好超市一樣,連樓上奶奶上個月都來過的景點,怎麼說也有點讓人洩氣。
至少我是膚淺地這麼認為。
今天就要跟各位介紹一個大隱隱於市的私房景點。不用搭3小時的公車在山路九彎十八拐,只要在參觀廟宇時,稍微抬頭注意一下,就能進入的奇幻世界。
一個由數學、宗教、日本文化構成的特殊景點,藏身在繪馬之中。
※San…gaku?
繪馬通常是拿來許願的,用途有點像擔心拜拜時神明沒聽清楚,在廟裡留下的N次貼。但要是稍微注意看,某些神社的繪馬堂裡,掛了許多大型的繪馬匾額。這些繪馬匾額,不僅是許願,也是貢品。人們畫上珍貴的事物(有點像燒一台賓士的概念),進貢給神明。

身為一位數學家,最珍貴的必然是自己的數學知識了。
因此,古代日本數學家準備的繪馬上,往往繪製了數學題目。大大小小的三角形、相切相割的圓形、直線,從課本中被移植到了寺廟的匾額中,增添了幾分神秘的色彩。
這種繪馬有個特別的名稱,稱為算額(さんがく:sangaku)。
發文不附圖,此風不可長。

這張照片是去年底我跟朋友在北野天滿宮找到的算額,相當不起眼地被掛在角落。幾年前來天滿宮時我似乎還曾坐在下方,卻從來沒注意到,頭上有一塊畫了十一道幾何題目的匾額。
※算額就是戰鬥陀螺?
數學是由討論圓與方形之間的關係而建構出來的學問,它是我們該學習的六藝中一種:禮、樂、射、騎、寫、與數。這些是人類獨有,動物不需要的技藝。武田老師自幼學習數學,在這間神社裡,他的弟子藉由奉上此枚算額,祈求神明保佑他們的數學能力能有所精進。
這是某塊算額的序言。
這段話不僅透露出當時對數學的重視,還顯示了日本數學家的師生關係,就好像其他日本技藝的流派,相當緊密、講究禮儀。日本擅長窮盡一項技藝,昇華為文化,例如茶道、書道、陶藝、圍棋等。江戶時代的日本數學家同樣具備這份的精神,以中國傳入的數學為基礎,建立了「和算」。
和算特別之處在於,和算家們喜歡透過出題、解題,像圍棋棋手一樣的對決。
只是,沒有網路的時代該怎麼交流題目呢?
就要靠「算額」。
和算家雲遊四海,到各地神社參拜時,會特別留意是否有算額可以挑戰。換句話說,這些算額就是和算家們的棋盤,他們的戰場。許多和算家窮盡一生,只為了解開對手的題目,或留下無人能解的經典遺題。
1817年到1828年間,和算家山口坎山遊歷日本各處神社,寫下一本遊記《山口坎山道中日記》,紀載了各式各樣的算額,目前是新瀉阿賀野市的有形文化財。我們可以想像,要是山口先生活在21世紀,應該會開個粉絲頁,每天上傳今天拍到的算額,底下附上詳解——然後只有三個人按讚。聽起來有點可憐。
事實上,可能更可憐。
他的日記裡有這麼一段話:
這道題目,我花了四到五年,總算再今年春天我才解出來。不過,這題目其實沒出得很好。我建議每一位學生,與其花時間解這種題目,不如去讀更多數學教科書吧。
也就是說,他的臉書應該是先拍照,寫下「噢噢,看到好題目可以挑戰了」。然後五年後他的朋友會看到「山口回應了他自己在2010年的一則動態」,點進去還是這麼一則抱怨的回應!

※算額的文藝復興
由於算額上繪製的圖案、數學描述並非任何人都能了解,被供奉在廟裡的算額常常會被忽略,許多寶貴的算額也因此消失。到1997年為止, 統計的現存算額僅約884面, 最近這幾年又新發現一些算額, 現存算額總數大約達到900餘面。
不過,這幾年算額在日本逐漸受到重視,某些中小學甚至將算額引入課堂中,作為綜合性的學習素材。老師利用算額,教導學生包括語文,工藝,美術,社會,歷史,數學等各種知識。比起課本,用算額學習應該會有趣許多,學生也能得到更多新的刺激,畢竟知識是整體性的,平常分門別類、切開來學習,偶爾也需要整體學習。
而說到這股算額的熱潮,免不了得提一位傳奇性的高中數學老師——深川英俊。
他原本在愛知縣的某所高中任教,投入大量的時間與精力,獨立研究算額,有了卓越的成果。起先在日本不受重視,但他不放棄,將研究成果寄給數位歐美知名學者,得到了英國幾何大師Dan Pedoe的賞識,兩人合著《Japanese Temple Geometry》。之後他又發表了幾本相關著作,包括代表作《Sacred Mathematics: Japanese Temple Geometry》 (日文版《聖なる数学:算額-世界が注目する江戸文化としての和算》)。現在受邀在日本名城大学擔任兼任講師,在算額這個領域有著重要的地位。不過,比起淵博的算額知識,深川老師對一件事物的全心投入,從無到有的奮鬥過程,我認為更值得學習。
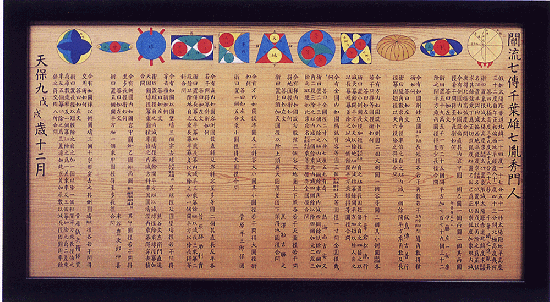
※算額尋寶之旅
要去日本旅行的朋友,除了訂房跟便宜機票網站外,我推薦另一個網站和算之館,它詳細記載了各都道府縣哪間神社、寺廟保有算額。
根據我的經驗是,就算知道哪間神社有,還是得花時間去找。因為很多神社對算額疏於管理,往往會和一般的繪馬擺在一起,充分體現了「藏葉於林」這句成語。好幾次,我站在底下拍照拍半天,也頂多有人探頭看看我在拍什麼,看兩下又離開,完全沒發現這個「數學古董」。事實上,我們還得感謝廟方的疏於管理,不然有些寺廟知道算額是重要文化財,就會收藏起來,怎麼找也找不到。
三百多年前,一群京都的和算家奉旨將一件秘密傳給後代。為了躲避幕府耳目,他們將這個秘密轉換成數學題目,寫在算額上,藏到祭拜學問之神的北野天滿宮。他們對自己的後人能破解算額,找出他們留下的秘密。然而繪師繪製時出了一個差錯,導致題目沒人能解得開。就這樣,三百年過去了……
各位今年去賞櫻賞楓時,如果時間允許的話,不妨加入一趟探訪算額的尋寶行程吧。

註:更多賴以威的數學故事,請參考《超展開數學教室》。