一個平凡的下午,工作累了捧著一杯剛煮好的咖啡走到陽台,看到的是對面大樓外牆排列得井然有序的長方形窗戶,和陽台邊的柵欄,一樣是有規律地重複著同樣的間隔。環顧我們的生活空間,好像規律性的結構無所不在,例如樑柱、磚瓦和地磚等等的各種人造物體,很容易地讓人誤以為只要是有規律的結構,一定就是人造的。而大自然中難道就不存在這樣的規律嗎?其實有的,最典型的例子就是晶體(Crystal)。
什麼是晶體?講講生活中常見的例子很多,料理中常用到的糖和鹽都是晶體,還有金屬、水晶和寶石等等。

意外發現不凡的晶體
一般人認為,晶體是所有固體最基本的特徵,並且是由「原子或分子按照一定的週期性,在空間排列成具有一定規則的幾何外形的固體。」至少很多教科書都還是這麼寫著。
但是在1982年的一項發現,顛覆了這個說法,而這個發現就是「準晶體(Quasicrystal)」。
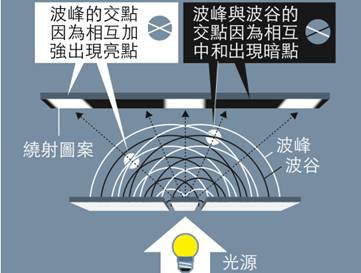
1982年四月的一天早晨,當時在美國標準技術研究所(NIST)客座研究的以色列籍科學家丹.舍特曼(Dan Shechtman)在實驗室中用晶體學觀測鋁錳合金時,發現了一個不可能出現的繞射圖(圖2)。繞射圖是材料學家常用的一種技術,他們用高能量的光線像是X射線或是電子束照在晶體上,當這些光線穿透過晶體後打在螢幕上,所得到的就是晶體繞射圖,而分析它就能夠得知這個晶體的型狀和結構。

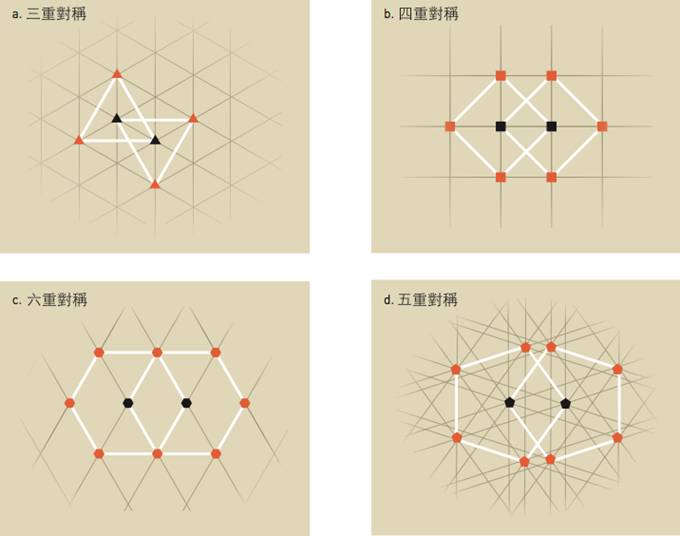
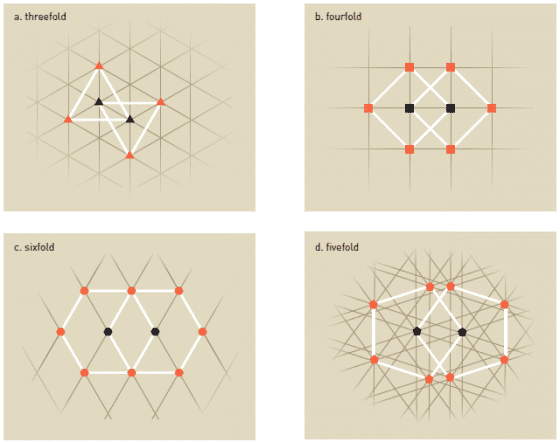
話說回來,為什麼舍特曼所觀察到的繞射圖不可能出現呢?因為長久以來,科學家認為晶體必須要是有週期性地排列,才能延續性地填滿整個平面或空間,而如圖3所示,某些幾何形狀像是五角形是不可能週期性地排列,所以被認定無法成為晶體。而舍特曼在實驗室裡看到的繞射圖顯示晶體擁有五角形的對稱性,正是先前科學家認為不可能存在的晶體結構。
舍特曼十分瞭解這個發現所蘊涵的意義,當下很興奮地從實驗室衝到外面走廊上,找人想要分享這個天大的消息,但是走廊上空無一人,他只好再乖乖地回實驗室做進一步地確認。接下來不管他用什麼方式去確認,證據都確實顯示了這個突破性的發現。
排山倒海而來的質疑

若你以為科學界會因為舍特曼的發現而歡聲雷動,那可就大錯特錯。當時所有科學家都強烈斥駁他的實驗結果,很多人第一時間斷定是實驗出錯才有可能得到這個結果。
而接下來兩年的時間,他不斷辛苦地捍衛自己的實驗結果,並持續承受其他科學家包括同事們的批評甚至輕蔑,嚴重到當時研究機構的負責人將他趕出團隊,認為整個團隊因他而蒙羞。另一位強烈的反對者是鼎鼎大名的物理學家,並且得過諾貝爾獎兩次的萊納斯.鮑林(Linus Pauling),他到死前都公開嚴厲地反對特舍曼的研究主張。
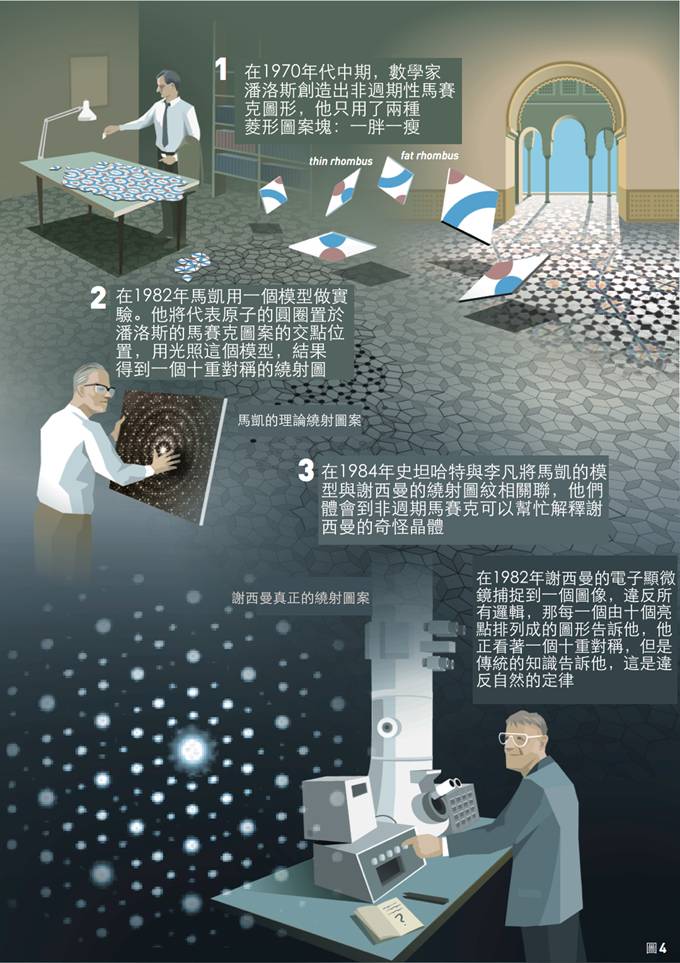
一直到兩年後,才陸續有科學家願意接受他的發現,並提出佐證。後續研究顯示,原來該晶體的結構跟另一種數學家所發現的結構相同,叫做「潘洛斯圖案(Penrose Tiling)」(圖5)。

準晶體的特性
潘洛斯圖案(圖5)是由英國劍橋大學的數學物理學家羅傑.潘洛斯(Roger Penrose)所發現。這個圖案有什麼樣的特性呢?其中很重要的就是它的對稱性。
這個世界所存在的對稱性分為三種,第一種對稱是所謂的「平移對稱(Translational symmetry)」,就是把一個圖案往某方向直線移動,如果它能和原來的圖案重疊,我們就說它有平移對稱性。除了平移對稱外,還有「旋轉對稱(Rotational symmetry)」和「鏡像對稱(Reflection Symmetry)」,前者是指你可以對著某中心旋轉圖案某固定角度,它能和原來的圖案重疊,而後者是指將圖案對著一條線對折後,圖案可以重疊。所有的對稱都可以用這三個項目來分類。
很特別地,潘洛斯圖案具有「五角形旋轉對稱(5-fold rotational symmetry)」和「鏡像對稱」,但是卻沒有「平移對稱」,也就是說它沒有一般科學家對於晶體所要求的週期性。這個圖形全由兩種菱形不斷地拼接而成,而且如果有人在一個固定面積裡數這兩種菱形的數目,它們的比例會剛好趨近於著名的「黃金比例(Golden Ratio)」。
舍特曼的實驗終於漸漸地被世界各地的科學家重複,並找到相同的結論。事實上很多人曾經觀測到它,但是卻因為不相信自己實驗的結果而放棄深入追究,所以這也告訴了我們相信自己的實驗是多麼重要。
後來科學家們不只驗證了舍特曼是對的,他們更發現了自然界中更多種合金材料有著相同的結構和對稱性,為了有別於以前傳統科學家對於晶體所下的定義,他們稱這種非週期性的晶體為「準晶體(Quasicrystal)」。科學家並發現,有擁這種結構晶體的合金材料特別堅硬。

這個革命性的發現改寫了所有的教科書。1992年國際晶體學協會把原先對於晶體的定義:「一個由原子、分子或離子,規律且重複性排列所組成的三維圖形」正式改為「任何具有干涉條紋的固體(Any solid having an essentially discrete diffraction pattern)」。舍特曼也因此在2011年獲得諾貝爾化學獎。
藝術與設計
造型和結構均是藝術和設計中不可或缺的元素,不管藝術家對什麼結構有興趣,它一定也被科學家研究過,反之亦然。因此,常常會看到晶體在藝術作品中出現。準晶體特別的對稱性讓它看起來不規律,但其中又暗藏著規律,是很多藝術家或設計師喜歡的圖案,也可以說是科學和藝術交匯的最佳範例。
台灣也看得到由準晶體所啓發的藝術作品。dr. i 今年(2014)在台北信義區的五星級飯店「寒舍艾美酒店(Le Meridien Taipei)」(台北市信義區松仁路38號) 內的一樓大廳,完成了一項動態光雕作品《潘洛斯之夢》,歡迎有興趣的讀者可以前去觀賞!
作品說明:「藝術家以英國天文物理學家羅傑.潘洛斯的潘洛斯圖案為發想,特地為台北寒舍艾美酒店量身設計的動態光影裝置。畫面由兩種平行四邊形所組成,圖案的律動與組合無限延伸,呈現科學與藝術的跨領域交匯,以及藝術家對宇宙間美麗定律的探索。」



參考文獻:
- The Nobel Prize in Chemistry 2011
- N. G. de Bruijn, “Algebraic theory of Penrose’s non-periodic tilings of the plane”, Mathematics, Proceedings A 84, 1, (1981)
- A. L. Mackay, “Crystallography and the Penrose pattern”, Physica 114A, 609, (1982)