數學圍繞在我們四周,它在許多方面型塑(shaped)我們對這個世界的理解。
作者|ANDY KIERSZ
編譯|蘇俊鴻
2013年,身為數學家,也是科普作者的伊恩.史都華(Ian Stewart)出版了《改變世界的17個方程式》(The 17 Equations that Changed the World)一書。近來,我們在Dr. Paul Coxon的Twitter (由數學輔導老師,也是部落客的Larry Phillips所註冊)上發現這個他摘錄書中方程式所成的簡便表格:
對於這些塑造數學及人類歷史的美妙方程式,下面有更多的介紹:
1) 畢氏定理:
這個定理是我們理解幾何的基礎。
它描述平面上一個直角三角形三邊之間的關係:兩個短邊(a和b)平方相加,可以得到長邊(c)的平方。在某些方面,這個關係確實將我們熟知的平面歐氏幾何和曲面的非歐幾何分開來。例如,畫在球面上的直角三角形就不用遵守畢氏定理。

2) 對數:
對數(函數)是指數函數的反函數。
一個特定底數的對數,告訴你用這個底數來表示這個數所需要的指數(power)。譬如10°=1,所以底數為10的1之對數log1=0;10¹=10,所以log10=1;10²=100,所以log100=2。方程式logab=loga+logb,展示對數最有用的應用:將乘法變成加法。一直到計算機發展之前,這是快速進行大數字相乘最常用的方法,大大地加快在物理、天文,以及工程上的計算。
3) 微積分:
這裏給的公式是微積分上導數的定義,導數是衡量兩個量之間變化關係的比率。
比方說,我們考慮速度,這是位置對時間的導數。假如你每小時用3英里的速度行走,表示你以每個小時3英里改變你的位置。一般而言,多數科學家有興趣的是瞭解事物如何改變,導數和積分,微積分另一個基礎,正是數學家與科學家理解變化的關鍵。
4) 萬有引力定律:
牛頓的萬有引力定律描述兩個物體間的吸引力F,由常數G、兩物體的質量m1和m2,以及兩物體之間的距離r而決定。
牛頓的定律是科學史非常出色的部份,它幾乎完美地解釋行星為何依照他們所遵循的方式移動。同樣出色的是它的普遍性,不只是適用於地球上的重力如何作用,或是在我們的太陽系,也包括宇宙的任何角落。牛頓的引力有效維持了200年,直到被愛因斯坦的廣義相對論取代為止。
5) -1 的平方根:
數學家總是在擴展數字到底是什麼的概念,從自然數,到負數、分數、和實數。-1的平方根(經常被寫作i),完成這個過程,並且引出複數。
在數學上,複數是非常優雅的。代數能完美依循我們所要的方式運作,任何方程式都有複數解,不一定有實數解:像x²+4=0沒有實數解,但它有兩個複數的解:±2i。微積分可以擴展到複數,經由這麼做,我們發現這些數字一些驚人的對稱性和性質,這些性質使得複數在電路和信號處理上變得不可或缺。
6) 歐拉的多面體公式:
多面體是多邊形三維的版本,像立方體就是其中一個例子。多面體的角落就稱為頂點,連接頂點的線段稱為邊,覆蓋它的多邊形就稱為面。
一個立方體有8個頂點,12條邊,和6個面。倘若將頂點數和面數加起來,再減去邊數,得到8+6-12=2。歐拉的公式指出,只要你的多面體是良態的(well behaved),將頂點數和面數相加,再減去邊數,你總會得到2。無論你的多面體有4、8、12、20或是任意面數,都將為真。歐拉的發現是現在被稱為拓樸不變量的最初例子之一,同類形狀所共享的某些數字和性質彼此都相似。良態的多面體都有V+F-1=2。這個發現,連同歐拉哥尼斯堡七橋問題(the Bridges of Konigsburg Problem)的解法,一起為現代物理學不可或缺的數學分支拓樸學的發展鋪好道路。
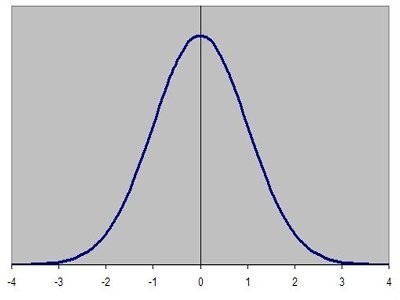
7) 常態分布:
有著熟知鐘形曲線圖形的常態機率分布,在統計學中無處不在。
物理、生物以及社會科學上經常運用常態分布來模式化各種性質,原因之一是常態曲線可以用來描述大量獨立過程(independent processes)的行為。
8) 波動方程式:
這是一個微分方程,規範波函數對時間與空間變數的二次微分的方程式,其中 C 代表波的傳遞速率。
波動方程式可描述波的行為,如振動的吉他弦,石塊丟出後池塘產生的漣漪,白熾燈泡產生的光等。波動方程式雖然只是一個微分方程式,解決這個方程所發展出的技巧開啟了理解其他微分方程的大門。
9) 傅立葉變換:
想要理解複雜的波動結構,像是人的說話,傅立葉變換是不可缺少的。
給定一個複雜、凌亂的波動結構,例如人的談話錄音,傅立葉變換允許我們將這凌亂的結構分解成一些簡單波的合成,大大地簡化分析的工作。傅立葉變換是現代信號處理和分析,以及數據壓縮的核心。
10) 納維-斯托克斯方程式:
和波動方程式相同,這也是一個微分方程。
納維-斯托克斯方程式描述流體的行為,水在管道的流動,空氣流過機翼,或是煙從點燃的香煙上升起。儘管利用電腦模擬流體運動,我們可以得到納維-斯托克斯方程式極佳的近似解,但能否構造出這個方程式數學的精確解,仍然是待解的問題(有百萬美元獎金)。
11) 馬克士威方程組:
這是由四個描述電(E)與磁(H)的行為和關係之微分方程所組成的方程組。
馬克士威方程組之於古典電磁學,如同牛頓的運動定律和萬有引力定律之於古典力學,他們是我們解釋電磁學在日常尺度下如何作用的基礎。如要推廣到原子的尺度,就有賴量子力學的修正,這門學問稱為量子電動力學。清楚的是,這些優美的馬克士威方程式是在人類尺度下,電磁學以及光學─光即電磁波─能夠被良好描述的近似方程組。
12) 熱力學第二定律:
在一個封閉的系統中,熵 (S) 總是保持穩定或逐漸增加,而波茲曼寫下的方程式更賦予了熵統計的意義。
簡單地說,熱力學的熵是度量一個系統的紊亂程度。一個開始時有序,但不平衡的系統,例如,靠近寒冷區域的熱點區域,總是趨向平衡的紊亂狀態,熱會從熱區流向冷區,直到均勻分佈為止。大多數的物理過程都是不可逆的,亦即宇宙的熵會一直變大,這隱含了時間是有方向性的。例如我們將冰塊放入一杯熱咖啡中,我們總是看到冰塊融化,卻未曾見過一杯咖啡生出冰塊而咖啡自己變熱。
13) 相對論:
愛因斯坦用狹義和廣義相對論從根本上改變了物理的進程,經典的方程式 E=mc² 說明質量與能量的轉換關係。
狹義相對論引進光在真空中的速度是固定不變的,以及不同速度移動的人對時間流逝及空間距離感受並不相同的概念。廣義相對論則認為重力是時間與空間本身的彎曲和摺疊,自牛頓的定律以來,這是我們對重力的理解首次巨大的改變,對於我們了解宇宙的起源、構造,和最終結局,廣義相對論是不可或缺的。

14) 薛丁格方程式:
這是在量子力學上最主要的方程式,如同廣義相對論在最大尺度上說明我們的宇宙,這個方程則是支配原子和次原子粒子的行為。
現代量子力學是歷史上非常成功的科學理論所有我們做的實驗結果都和量子力學的預測完全一致。最現代的技術也需要量子力學,舉凡核能、肇基於半導體的電腦,以及雷射等都建立在量子現象上。
15) 資訊理論:
這裏給出的方程式是為了夏農資訊熵(Shannon information entropy)。
如同前述,熱力學的熵是對紊亂的一種度量,這裏指的是對訊息資訊量的度量,一本書,一張網路上寄送的JPEG圖片,或是任何可用符號表示的事物。訊息的夏農熵說的是在不漏失內容的情形下,訊息可以被壓縮多少的下限。夏農的熵度量引起資訊理論的數學研究,他的成果是今日我們如何在網路上溝通的核心。
16) 混沌理論:
這個方程式是梅的二次多項式映射(May’s logistic map),它描述一種通過時間演變的過程 ─x的下一個時間世代 xτ+1─ 由方程式的右邊給出,依賴x目前的世代xτ。
k是一個選擇的常數,對於某些k值,映射會顯示混沌的行為:如果從某些特殊的初始值x開始,過程將演化出一種結果,如果由其他的初始值開始,甚至非常非常靠近第一個值,過程將演化出完全不同的結果。我們所見的混沌行為,對初始條件非常敏感,在許多領域都是如此。天氣是個典型的例子,大氣條件的一個微小改變可以導致幾天後完全不同的天氣系統,這個概念最常提及的說法就是「蝴蝶效應」。
17) 布萊克-休斯方程式:
另一個微分方程,布萊克-休斯方程式描述金融專家和商人如何找到衍生性商品的價格。
衍生性商品,基於某些潛在資產的金融商品,例如股票,一個現代金融體系的主要部份。布萊克-休斯方程式允許金融專家利用衍生性商品的特性和潛在資產來計算這些金融商品的價值。

—
資料來源:The 17 Equations That Changed The Course Of History
譯者:蘇俊鴻 現為北一女教師。
責任編輯:臺大物理系 王名儒教授











































