- 作者/林家妤 Sharkie Lin,因為數學成為斜槓青年,進行數學藝術創作、策展、採訪、寫作、創意教學、博物館規劃,希望能為世界帶來一點樂趣。
Take Home Message
- 德摩根來自一個學識豐富的家族,其父親奧古斯都.德摩根為德摩根定律的發明者。
- 數學是德摩根創作的核心,他的數學家父親啟發他在設計中創作出崇高的對稱、形狀、圖樣。
- 德摩根的許多圖案和設計都以對稱組織而成,吸引觀者眼睛看向清晰的中心對稱軸。
- 從方形鋪磚到圓形瓷盤,德摩根在他所有的平面設計中都考慮到構圖的形狀。每片瓷磚設計也都經過數學考量,因此當瓷磚安裝在牆上時,各種設計元素就能互相匹配,並創造出美麗且結構良好的圖案。
德摩根(William De Morgan)是英國維多利亞時代的瓷器設計師,他多以奇妙的生物和花卉、蔓藤花紋作為創作題材,其作品的想像力非常豐富,並且深受伊斯蘭藝術與中東陶瓷設計的影響。這個特別的姓氏是否讓你覺得很熟悉呢?

擁有大數學家父親的瓷器設計師
德摩根來自一個學識豐富的家族,他的父親是奧古斯都‧德摩根(Augustus De Morgan),這位就是鼎鼎大名的德摩根定律(De Morgan’s laws)發明者!奧古斯都‧德摩根是倫敦大學學院(University College London, UCL)第一位教授,同時也是倫敦數學協會(London Mathematical Society)的第一任主席;而他最著名的學生,就是被譽為首位程式設計師的勒芙蕾絲(Ada Lovelace)。
德摩根的母親蘇菲‧弗蘭德(Sophia Elizabeth Frend)則是英國作家與社會運動者,她廣泛撰寫了她熱情支持的社會問題,例如監獄改革、反活體解剖、廢除奴隸制。而德摩根的外公威廉‧弗蘭德(William Frend)則是一位神職人員、社會改革者與數學家;其胞弟喬治後來成為了一名數學家,胞妹瑪麗則是童話故事的作者。
繪畫是德摩根最初的藝術追求,本可以讓他進入更安靜的創作生活,但在德摩根遇見他的終身好友莫里斯(William Morris)之後,他便從學校退學放棄成為藝術家,轉而成為追求技術革新的設計師。
德摩根對技術充滿好奇,常進行化學研究創造新的光澤釉,以及精心研發創新的上釉、燒製及上色技術,製造彩色玻璃和陶瓷讓他著迷,他甚至還設計並製造了自己的窯爐,成立自己的公司為好友莫里斯製作作品。此種強調藝術與手工藝的結合,影響了英國美術工藝運動。
現今倫敦維多利亞與亞伯特博物館(Victoria and Albert Museum, V&A)的文創商品中,依然販售許多莫里斯的花紋圖樣設計。V&A 裡頭也收藏了大約 1200 件德摩根的作品,這兩位威廉為英國留下了許多美妙的幾何設計。
由於德摩根長年專注於光澤器物的研發,未能更新他的圖樣設計以至於過時,加上他對於經營公司沒什麼興趣,公司因而倒閉;而後健康狀況不佳的德摩根便去義大利過冬,並在配偶的鼓勵之下開始寫小說。他不放棄自己的創作之旅,不但減緩了心中的憂鬱,更在 65 歲的時候成為受大眾歡迎的作家。
德摩根的配偶艾芙琳(Evelyn De Morgan)在繪畫上有卓越的成就,內容常使用精神、神話、寓言主題突出女性身體,用以表現精神主義與女性主義。德摩根於 48 歲時與小自己 16 歲的艾芙琳結婚,他們在靈性研究和體驗上有共同興趣,並且相信他們的藝術可以永遠為每個人創造一個更美好、更美麗的世界。
兩人過世之後由艾芙琳的姊妹斯特林(Wilhelmina Stirling)成立了德摩根基金會(De Morgan Foundation),整理德摩根夫婦兩人超過上千件作品,包括陶瓷、油畫、素描等,目前在 3 個地方有長期合作展出,相關地點列於文末。
「崇高的對稱」展覽
介紹完本文主角德摩根與其家族、朋友之後,來看看德摩根基金會為數學與文化策劃的展覽「崇高的對稱:德摩根瓷器設計背後的數學」(Sublime Symmetry: The Mathematics behind De Morgan’s Ceramic Designs)吧!
這檔展覽最初於 2018 年 5 月~10 月於倫敦市政府的市政廳藝廊(Guildhall Art Gallery)展出,筆者正好在 2018 年夏天至倫敦旅行,並且有幸在隔年訪問瓦茨美術館-藝術家村(Watts Gallery – Artists’ Village),與本檔展覽的策展人哈迪(Sarah Hardy)對談。
策展人哈迪表示,相較於過往以藝術與心靈的角度詮釋德摩根夫婦的作品,這回的策展緣由是來自一位挫折的數學教師朋友。這位友人抱怨教授歷史的同事可以帶著孩子去城堡與豪宅校外旅行,但是自己教的數學卻只能被限制在教室中,希望能夠點燃學童對於數學的熱情。
因此策展人便策劃了一檔與「數學」有關的藝術展覽,又因為德摩根家族與倫敦數學協會有深厚的歷史淵源,讓這一切變得相對容易,也使得過往以詮釋藝術作品為主的策展人,能夠透過嚴謹的數學檢驗與嶄新的幾何視角,向大眾介紹德摩根的作品。
哈迪提到有次在展場一個孩子看了德摩根的瓷器,說道:「圖案中間有一條線耶,兩邊長得一樣。」提醒了她德摩根作品的幾何設計強烈可見。而這檔展覽的內容正好適合英國學生學習歷程的第二階段(key stage 2, KS-2)階段,也就是 7~11 歲的孩子學習。同時策展單位也在官網提供教育素材包,供教師引導學生學習幾何形狀與規則。
數學是他創作的核心,數學家父親啟發德摩根在設計中創作出崇高的對稱(symmetry)、形狀(shape)、圖樣(pattern)。接著,我們就以這 3 大面向介紹德摩根的幾何設計。
- Symmetry 對稱
「對稱是變化中的不變。」(Symmetry is “Change without Change”)
-韋爾切克(Frank Wilczek),2004 年諾貝爾物理學獎得主
在藝術中,「對稱」普遍被認為是美的代名詞。這種數學工具可以透過反射、旋轉、縮放來變換設計,但不改變其他屬性,因此對稱可以說是變化中的不變。關於對稱的各種基本變換,可見筆者發表於《科學月刊》第 623 期〈發現臺灣日常文化中的幾何元素─花磚幾何學〉的文章。
德摩根的許多圖案和設計都是以對稱組織而成,吸引觀者眼睛看向清晰的中心對稱軸。這條線,賦予了精心設計的圖樣能呈現出各種不同表現型式,像是花卉圖案和起伏的樹葉捲曲,因其對稱排列而顯得富含結構與秩序。

- Shape 形狀
德摩根曾經說過,古希臘數學家歐幾里得(Euclid)的著作是最引人入勝的文學作品,顯示了他對於形狀的性質與結構深感興趣。
從方形鋪磚到圓形瓷盤,德摩根在他所有的平面設計中都考慮到構圖的形狀。每片瓷磚設計也都經過數學考量,因此當瓷磚安裝在牆上時,各種設計元素就能互相匹配,並創造出美麗且結構良好的圖案。
在德摩根精心設計的瓷盤邊界和圖案邊緣,也可以看到連續的圓形圖樣。他從伊斯蘭幾何設計中借用了這種裝飾技巧,這種圓形圖案代表了「阿拉的無限本質」,因為它們沒有開始也沒有結束,可以被無止境地追隨。德摩根控制了這些圓圈的特性,以確保他的邊界設計符合比例。

此外,圓形對稱也為德摩根的平面設計增添趣味和活力。圍繞瓷盤邊緣旋轉的圖樣,使得觀者的視線能圍繞著設計呈現美妙的圓形運動,讓他的奇幻動植物看起來更加栩栩如生。
- Pattern 圖樣
這些複雜幾何圖樣的設計,往往需要具備嚴謹的幾何學知識,才能想像將單一瓷磚的圖樣設計重複覆蓋整面牆的結果。當設計圖樣完整呈現時,便可以充分欣賞德摩根設計的精華,就像是他在倫敦萊頓屋博物館阿拉伯廳(Arab Hall, Leighton House Museum)裡輝煌的瓷磚設計。
要如何思考這麼大尺度的瓷磚設計呢?德摩根首先會先在紙上繪製他的大型瓷磚設計方案,並使用比例和複雜的測量方法以確保這些設計能成功,然後再將它們應用到物理瓷磚表面。
由於他的繪圖技能與天生對於數學的理解能力,使得他的花器作品能巧妙在設計中運用數學。德摩根利用他對視覺和空間的感知,藉由控制二維圖面,即使圖樣轉換到擁有複雜形狀表面的花瓶與花盆上,還有塗在陶瓷表面上時,也都能完美符合三維物體的每條曲線。因此他可以創造出美麗的設計,並且與花瓶或盤子本身相互呼應。
這檔展覽除了介紹德摩根的幾何設計外,展場中還有一些別出心裁的互動小遊戲,例如將德摩根的設計圖樣製作成puzzle 15 數字推盤遊戲。首先將原本的圖樣分割成 4×4 的 16 個方塊,而後取走角落的方塊,並滑動剩餘的 15 個方塊打亂圖案。看看你能不能拼回來原本的圖案?

此外,本次辦理展覽的倫敦數學協會也提供了一些有趣的展品,像是早期收藏的木製數學模型,以及各式立體的潘洛斯平鋪(Penrose tiling)等多元的立體幾何模型,讓觀眾對於數學視覺化更有感覺。
德摩根無疑是英國融合數學與設計的始祖之一,正在閱讀這篇文章的你,若是下回有機會拜訪英國,不妨也循著德摩根的蹤跡,來趟具有深度的數學文化走讀之旅。
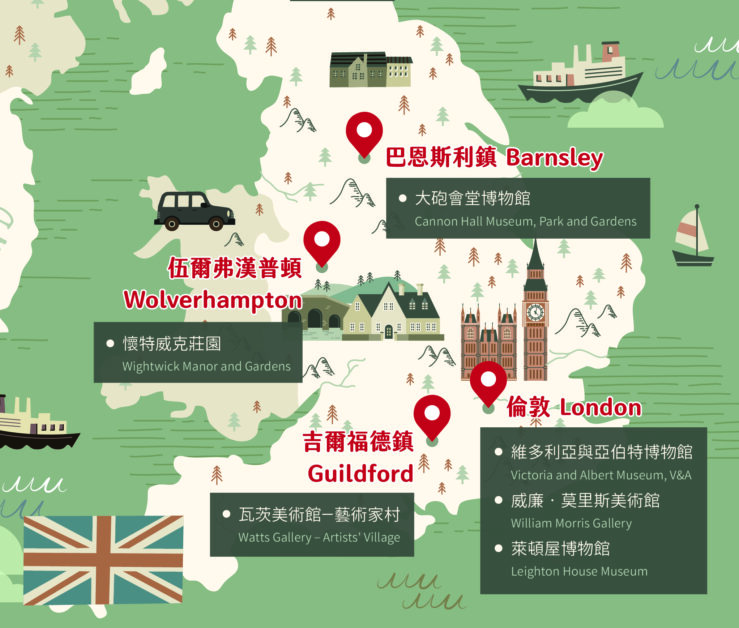
看完文章,你是否也想來趟英國幾何文化之旅呢?
以後若有機會,不妨照著下方的地圖走一趟英國,感受一下數學與藝術融合的氛圍吧!
| 想了解更多德摩根的作品,也可以參考《崇高的對稱》展覽手冊, 或到德摩根基金會官網看看哦! |  |
延伸閱讀
- 德摩根基金會官網:https://www.demorgan.org.uk

- 〈本文選自《科學月刊》2022 年 2 月號〉
- 科學月刊/在一個資訊不值錢的時代中,試圖緊握那知識餘溫外,也不忘科學事實和自由價值至上的科普雜誌。