文/蔡天新,本文摘錄自《數學的故事》,2019年時報出版
有些數學證明如此美妙,只能是上帝的創造,數學家不過是幸運地發現了它們而已。
——艾狄胥
探險家和作家雷利
沃爾特.雷利(Sir Walter Raleigh)是十六世紀後期英國著名的探險家,算得上是當時的風雲人物。他本是女王伊莉沙白一世的寵臣,三十一歲受封為爵士,後來被女王的繼任者詹姆斯一世指控謀反並囚禁於倫敦塔,最終被處以極刑。

雷利少年時即參加法國宗教戰爭,後就讀牛津大學,畢業後又參與鎮壓愛爾蘭人的起義。他坦率批評英國對愛爾蘭人的政策,引起了伊莉莎白女王的注意。女王欣賞雷利的才幹,也被他的個人魅力吸引。
伊莉莎白女王賜予雷利倫敦特勒姆旅館的部分租借權、各色絨呢的出口權,讓他擔任錫礦主管、海軍中將和議員,乃至王宮侍衛長、英吉利海峽的澤西島總督。後來雷利瞞著女王與她的侍女偷偷結婚生子。女王發現後,把他和妻子雙雙關入倫敦塔,雖然不久後就釋放了他們,但雷利從此失去了比他年長二十一歲、終身未嫁的女王的恩寵。
雷利為了航海曾學習數學,也學過化學和醫術。與女王決裂之前,他曾遠距指揮在美國的北卡羅萊納和維吉尼亞建立殖民地。北卡羅萊納沿海的羅阿諾克島原本是英國人在新大陸最早的定居點,可惜一百一十六名移民某天卻突然人間蒸發,包括在新大陸誕生的第一名英國嬰孩維吉尼亞.戴爾(Virginia Dare),至今依然是未解之謎。那時距離「五月花」號駛往麻薩諸塞尚有半個多世紀。

如今,北卡羅萊納州的首府羅利就是以雷利的名字命名,羅阿諾克島上也有羅利堡國家歷史遺址,該島隸屬的縣名叫戴爾,即以那位新生兒的名字命名。有趣的是,同屬戴爾縣的小鷹鎮是一九○三年十二月十七日萊特兄弟首次成功試飛飛機的地方,小鷹鎮的沙洲與羅阿諾克島相距不超過十公里,中間隔著羅阿諾克海峽。
寫到這裡我想順便說,人名、地名、物名的中文譯名各異相當常見,例如義大利汽車製造商費拉里和他生產的跑車、賽車法拉利其實源於同一個單詞 Ferrari。而叫費拉里的義大利人中,還有十六世紀的一位助理醫生,他因為率先提出四次方程的代數解,成了那個時代最偉大的數學家之一。
一五九四年,雷利聽說南美洲有金礦,決定再次出海。他懷疑上一次的殖民行動之所以失敗,是因為彈藥不足以致全軍覆沒,這次打算準備足夠的食物、淡水、火藥、槍彈和炮彈。
那時的炮彈均為直徑相同的鐵球,雷利為此命令他的科學顧問、數學家哈里奧特(Thomas Harriot)找出在有限空間內盡可能堆放炮彈的方法,並計算船隊的彈艙能夠堆放多少發炮彈,由此產生了堆球問題和克卜勒猜想,我們將在後文中介紹。

雷利率領的遠征軍抵達蓋亞那以後,沿奧利諾科河航行到西班牙殖民地的腹地。奧利諾科河是南美洲四大河流之一,發源於委內瑞拉與巴西接壤處,上游是哥倫比亞與委內瑞拉的界河。
二○○○年我第一次去哥倫比亞時,搭乘的飛機便是從此河入海處進入南美大陸。西班牙人的文件和印第安的傳說使雷利相信,南美洲有一座「黃金之城」。他的確也找到了一些金礦,但沒有一處足以讓他殖民開發。
返回英國後,雷利出版了《蓋亞那的發現》一書。在他被處死(與他冒犯了英國國王不願得罪的西班牙人有關)以後,人們發現雷利還有許多文學著作,包括五百六十行遺詩。詩中他稱伊莉莎白女王為月亮女神,但也指責她絕情,很可能是影射她將他囚禁一事。此外他還寫了一些散文與一部《世界史》(從創世紀一直寫到西元前二世紀)。
蓋亞那位於南美大陸東北部,西鄰委內瑞拉,南接巴西,東邊是說荷蘭語的蘇利南和說法語的法屬圭亞那,雖然人口只有七十多萬,國土面積卻幾乎與英國本土一樣大。如今,可能會讓雷利比較欣慰的是,蓋亞那不僅是英聯邦成員國,也是拉丁美洲二十個國家裡唯一以英語為官方語言的。而在日本著名漫畫《海賊王》裡,雷利變成了海盜,而且只是個副船長,後來還成了鍍膜匠。
家庭教師哈里奧特

現在我們來說說隨雷利遠征蓋亞那的首席科學顧問哈里奧特。哈里奧特出生於牛津,就讀牛津大學的聖瑪麗學堂,在學生時代就展現出超凡的數學才能,畢業後不久就進入雷利家,成為一名家庭教師。
哈里奧特參與了雷利家族船隻的設計,並用自己的天文學知識為導航提供建議。一五八五年,雷利派他參加新大陸的羅阿諾克島探險,聘他為科學顧問,主要負責測量。
哈里奧特繪製了後來被稱為維吉尼亞州和北卡羅萊納州的地圖,考察報告出版後也多次重印。返回英國後,哈里奧特受雇於著名的珀西家族成員、諾森伯蘭九世伯爵,在伯爵家成為多產的數學家、天文學家和翻譯家,尤其擅長翻譯印第安人的阿爾岡昆語。
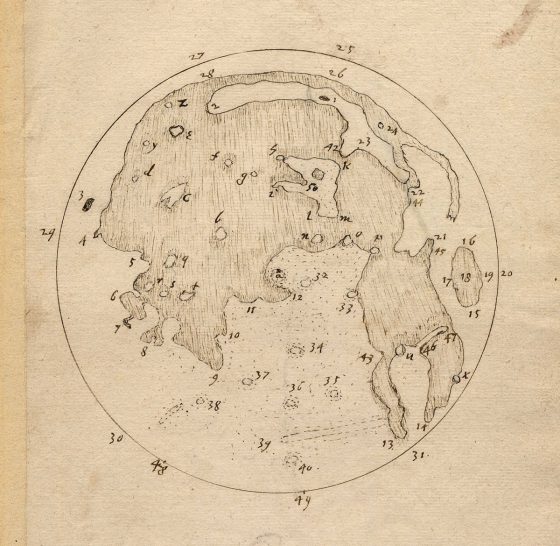
哈里奧特率先繪製出月球的地圖,日期標注為一六○九年七月,比伽利略早了四個月。一六○七年哈雷彗星的回歸也引起了哈里奧特對天文學的關注,他自製(另說購買)了一架望遠鏡,與伽利略各自獨立發現了太陽黑子和木星衛星。
他還率先發現了光的折射理論,只不過沒有發表。哈里奧特生前已是享有盛譽的天文學家和數學家,一九七○年,月球的一個隕石坑以他的名字命名。
身為數學家,哈里奧特被公認是英國代數學學派的奠基人,他在該領域的巨著《使用分析學》(Artis analyticaepraxis)在他去世十年後才出版。
書中改進了方程理論,注重根與係數的關係,詳細論述了如何由已知根建構方程式,並揭示出任何 n 次方程與 n 個線性方程之積是等價的,接近高斯在十九世紀證明的代數基本定理。特別的是,哈里奧特還創造了不等號「>」和「<」,這兩個符號也沿用至今。
如何在最小空間內堆放最多炮彈?
前文提到,雷利要求哈里奧特找出在有限船艙內堆放最多炮彈的方法。哈里奧特很快就給出了答案:先以三角形狀排好最低一層,然後讓第二層的球心盡可能地低,依次增加層數,就能得到一個盡可能最高效率的堆疊法。
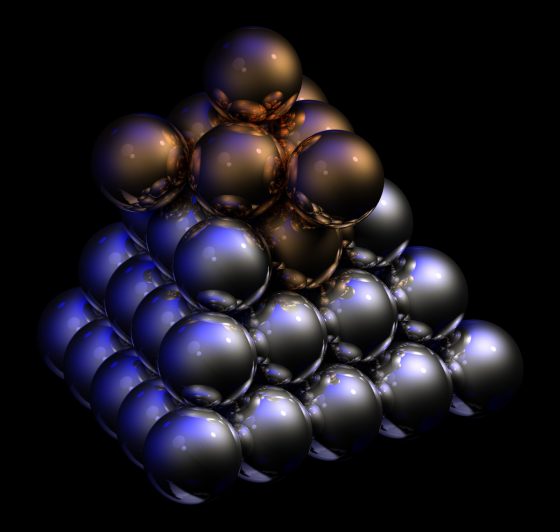
我們從中可輕易看出,按照這樣的堆放方式,每個非邊緣的炮彈恰好與十二顆炮彈相切,即同層六顆,上一層和下一層各三顆。關於一顆球能否與十三個同樣大小的球相切,一個世紀以後,牛頓與蘇格蘭天文學家格雷果里(James Gregory)有過爭論,牛頓的否定答案無疑是正確的。
這十二個切點形成的十二面體包緊了一個球體,所有這些十二面體可以填滿整個空間。把十二面體分成十二個全等的錐體,可以求得它的體積為 \(4\sqrt{2}\)。再按照阿基米德的球體積計算公式,每一顆球的體積是 4π/3。兩者相除即得球堆的密度為 \( \frac{\pi}{\sqrt{18}}\)。德國人克卜勒則給了更簡潔的方法,我們將在下節介紹,現在先來看平面的情形。
假如我們考慮二維的問題,即在平面上填塞圓。首先,我們讓每一個圓與四個同樣大小的圓相切,那麼在 m 行 n 列個圓的長方形排列中,圓的面積總和為 mnπ,而長方形的面積為 4mn,於是兩者的比值為 π/4。不難看出,只要平面的範圍(相比小圓的半徑)夠大,那麼小圓的半徑大小不影響這一比值。
其次,我們讓每一個圓與六個同樣大小的圓相切,由畢氏定理可知,每行圓的高度為 \(\sqrt{3}\),但每隔一行會減少一個圓,因此圓面積總和為 \(\frac{m\left ( 2n-1 \right )\pi }{\sqrt{3}} \),而長方形的面積仍為 4mn,於是兩者的比值趨近於 \( \frac{\pi}{\sqrt{12}}\),比第一種排列方式更緊密。當然,無論哪一種,都比空間球的堆積密度要大。
哈里奧特也是一位原子論愛好者,該學說源於古希臘哲學家德謨克利特(Demokritos)。德謨克利特相信,萬物的本原是原子,原子是一種不可分割的物質微粒,且毫無空隙。哈里奧特認為,研究球的堆放問題有助於理解物質的結構和組成。
一六○一年前後,他寫信把這個想法和堆球問題告訴了比他年輕十一歲、正在布拉格擔任羅馬帝國皇家天文學家的克卜勒,不巧那會兒克卜勒正埋頭研究天體理論,沒有太多興趣和時間考慮微觀世界。
克卜勒的雪花和猜想

一五七一年某個冬日,克卜勒出生於德國西南部的符騰堡公國(現巴登 – 符騰堡州的一部分),與愛因斯坦可謂正宗老鄉。他是一樁不幸婚姻的早產兒,父親是庸碌的傭兵,母親是一家小酒館老闆的愛吵架女兒。克卜勒身材矮小、體弱多病,但天資聰穎,幸運獲得了符騰堡公國領主專為貧困家庭的聰明孩子設立的豐厚獎學金,否則可能根本沒機會接受良好的教育。
克卜勒十六歲時進入圖賓根大學,之後屢獲幸運女神眷顧。首先,他的天文學老師是德國唯一一位堅信哥白尼「日心說」的人。
其次,在他拿到文學學士和碩士學位,準備成為牧師時,奧地利格拉茨市某間中學剛好需要一位數學老師,他在學校的推薦下前往補缺。再次,隔年夏天二十三歲的克卜勒在幫學生上課時,腦袋裡忽然閃過一個奇妙的念頭。
如前文所言,古希臘人只知道有四面體、六面體、八面體、十二面體和二十面體這五種正多面體(柏拉圖多面體),從畢達哥拉斯到柏拉圖都信奉「數學和諧論」,這一點啟發了克卜勒,深信行星的運行軌跡也應該是完美的幾何圖形。
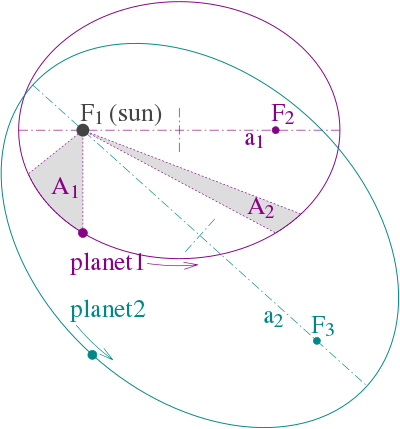
四年後,他發現了行星運動的第一定律和第二定律:所有行星分別在大小不同的橢圓軌道上運行;在同等的時間裡,行星的矢徑在軌道平面上掃過的面積相同。這兩個定律以及後來發現的第三定律,為克卜勒贏得了「天空立法者」美名。
一六一一年,也就是收到哈里奧特來信五年後,克卜勒出版了小冊子《六角雪花》(The Six-Cornered Snowflake)。

他不僅在書裡解釋了雪花為什麼是六角形,還探討了諸如蜂窩的結構、石榴果實為何是十二面體等現象,是最早從幾何出發研究自然的著作之一。克卜勒認為,雪花之所以呈六角形,是因為一個圓盤最多能與六個相同的圓盤相切,正六邊形可以平鋪整個平面。
尤其值得一提的是,正是在這本書裡,克卜勒提出了一個著名的猜想。
克卜勒猜想
在一個容器中堆放同樣的小球,所能得到的最大密度是 \( \frac{\pi}{\sqrt{18}}\)。
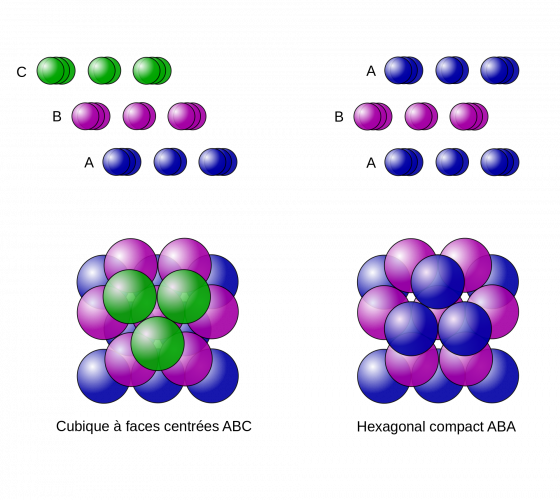
克卜勒是這樣敘述球體堆放方法的:考慮一個邊長為 2 的正方體,它的體積為 8。分別以它的全部八個頂點及全部六個面的中心為球心,以 \( \frac{\sqrt{2}}{2}\) 為半徑作十四個球體,由畢氏定理和每個面的對角線長為 \(2\sqrt{2}\)可知,每個面中心的球體與該面尖角上的四個球體剛好相切。
這樣一來,在這個正方體內,球體佔有的體積等於四個球體的體積(八個角,每個角有1/8個球體;六個面,每個面有1/2個球體)。故而密度是
\(\frac{4\left ( \frac{4}{3}\pi \left ( \frac{\sqrt{2}}{2} \right )^{3} \right )}{2}= \frac{\pi }{\sqrt{18}}= 0.740480…\)
雖然在上述方法中,正方體內沒有一個完整的球,但若換成一個大箱子,以這些正方體為基本單位來填滿箱子時,不完整球體的體積與中間那許多完整球體的體積相比就是微不足道的。同樣道理,箱子的形狀也不會影響密度。然而,克卜勒猜想的充分性卻難以證實。
一八三一年,「數學王子」高斯證明了克卜勒猜想在「格點型」的特殊情形下是成立的。所謂格點型是指用座標表示時,所有球心也落在座標和偶數整點上。
一九○○年,德國數學家希爾伯特(David Hilbert)在巴黎國際數學家大會上提出了二十三個有待解決的問題,其中第十八個問題的第三部分就涉及堆球問題。
從那以後,有許多數學家(包括美國華人數學家項武義)都曾宣布、發表或以為自己證明了克卜勒猜想,但都未能獲得一致的認可。
二○○五年,美國《數學年刊》發表了一篇長達一百二十頁的論文,宣布克卜勒猜想已經獲得證明。該篇論文的作者是美國數學家赫爾斯(Thomas Hales),他在著名的「朗蘭茲綱領」問題上有過重要貢獻。赫爾斯將堆球問題分為五千多種情況,考慮了十萬多個線性規劃問題,他的電腦程式運行了兩年,其複雜性超過一九七六年地圖四色問題的證明。
一個顯而易見的現象是,絕大多數幾何學家都不懂電腦程式,而電腦專家又難以理解深奧的幾何學。就連審稿小組的負責人都承認,他們對於這篇論文的正確性只有 99%的把握。鑑於此,我們繼續期待(如同期待費馬定理)將來會有更簡潔有效的證明方法。
——本文摘自《數學的故事》,2019 年 5 月,時報出版。