文/張明強副教授|國立中興大學物理系
2016 年 10 月 4 日,諾貝爾物理獎頒給美國華盛頓大學的 David J. Thouless , 布朗大學的 J. Michael Kosterlitz 和普林斯頓大學的 Duncan M. Haldane,三位得獎人均為英國出身。得獎的理由是「拓樸相變和拓樸物質的理論研究發現。(For theoretical discoveries of topological phase transitions and topological phases of matter) 」
拓樸性質起源於數學的研究,也就是在幾何學之外,研究物體被連續變化(比如說延展或彎曲),在不撕開或黏合或挖洞的狀況下,如何從一種幾何形狀變成另外一種幾何形狀的研究。
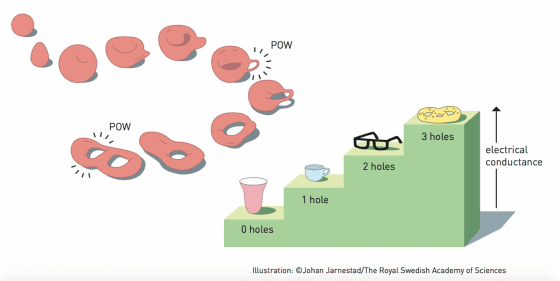
舉例來說一顆球和一個四方體拓樸性質一樣,可以想像球體不斷的變化之後,就可以變成四方體;而中間有一個洞的甜甜圈,拓樸性質和咖啡杯拓樸性質一樣,因為經過連續變化,甜甜圈可以變成有一個洞把手的咖啡杯。

本來拓樸學和物理學關連並不大,直到 Thouless 和 Kosterlitz 開始研究二維古典系統的二階相變,事情才開始變化。在他們的研究之前,一般人對二階相變的了解,都是來自於金寺堡-藍道定理(Ginzburg-Laudau Theorem)。我們可以考慮一個磁性系統,鐵磁的產生是要有所有小磁鐵磁場指向同一個方向,而順磁性的相態來自於小磁鐵磁場的方向都不一樣,平均起來磁性就為零,我們稱這種小磁鐵磁場都指向同一方向為「對稱性破缺 (Symmetry breaking)」。金寺堡-藍道定理完全奠基於對稱性破缺。而二維古典系統,基本上在有溫度的情形下,因為熱漲落 (thermal fluctuation)非常強大,所以沒法形成對稱性破缺,因此大家的認定是不會有相變的存在。
這樣的情形也可以由物理量的相關性(correlation)來理解。同樣考慮磁性系統,我們可以考慮相距離很遠的小磁鐵(也稱為自旋)彼此間的相關性,相關性可以理解為當我改變一個自旋,另一個(遠距離)自旋跟著改變的量。我們發現三維鐵磁性(也就是有對稱性破缺)的相態中,兩個距離相當遠的自旋量相關性是一個常數。但在二維磁性系統裡,遠距離自旋相關性會慢慢接近零。且慢,接近零有兩種接近的方式,一種是多項式的接近零,一種是指數的接近零,多項式的接近零(比如說 r-2) 比指數的接近零(比如說 e-r) 要來的慢許多,因此這裡面暗藏著玄機。
Kosterlitz 和 Thouless 發現,非常低溫的時候,是多項式的接近零。遠距離鐵磁的相關性是多項式的接近零。然後慢慢增高溫度,系統會產生渦漩,而且不是一個一個產生,每次產生都成對,而且方向相反。我們稱為正渦漩或反渦漩,見圖一。正反渦漩會成對出現成對,剛開始出現不會影響鐵磁的相關性,但溫度越高,渦漩越來越多,溫度高到一個程度,渦漩不再成對出現,而是單獨出現,且渦漩改變遠距離鐵磁的相關性,從多項式變成指數接近零。這樣的相變,並不會有對稱性破缺,而是相關性的改變,我們稱為「KT 相變」,圖 1 顯示的就是這樣的相變圖。
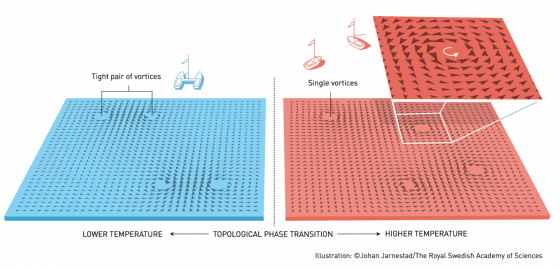
渦漩其實就是一種拓樸態,就像颱風一樣,渦漩有一個很像颱風眼的構造,此種構造就是類似甜甜圈的洞,我們稱為奇點,見圖中放大區域。Thouless 和 Kosterlitz 是第一位利用拓樸性質來解釋相變。 後來發現不管在一為或二維系統,比如說超流體相變,KT 相變非常重要。也解釋很多低維度系統相變得產生,改變人們對相變的了解。
拓樸物質其實不容易發現,「量子整數霍爾效應」和「分數霍爾效應」在八零年代一一被發現,而且獲頒諾貝爾物理獎。Thouless 也持續對拓樸態有進一步的了解,尤其是量子霍爾效應的解釋。Thouless 藉由對於拓樸學的了解,將量子霍爾效應跟所謂的「陳省生數」(Chern Number)連結起來。陳省生數可以類比為幾何體有多少個洞,而電子的導電率正比於陳省生數,也就是洞的數目,見圖 2。由此增進對拓樸物理學的深層了解,因此他獲頒此次諾貝爾物理獎一半的獎金。
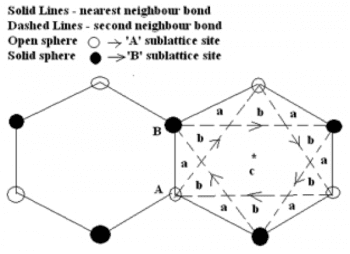
量子整數和分數霍爾效應這兩種物質都需要磁場形成藍道層。Ducan Haldane 在八零年代提出思考一個問題,就是能不能不用均勻磁場,保持移動對稱性來形成霍爾效應。他提出一個簡單的模型,就是在六角蜂巢模型中技巧加入次近鄰的作用力,如圖 3,破壞時間反轉對稱性 (time reversal symmetry) ,就可以不用加均勻磁場產生陳省生數等於一或負一的霍爾效應。
Haldane 另一個重要的貢獻,是發現一維系統的磁性拓樸系統。低維度系統,尤其是低維度的量子系統,量子效應要比三維系統來得大。Haldane 首先意識到,一維的磁性系統,由於量子漲落(quantum fluctuation)或是量子糾纏(quantum entanglement)非常大,因此產生奇特的現象。因此他開始提出自旋量為一的一維磁性系統,發現這個系統具有拓樸性質,稱為 Haldane 相態。這是第一個用理論提出的拓樸材質,而且馬上被實驗驗證。這種拓樸材質非常穩定,具有某些對稱性,也就是說一些雜訊只要不破壞這種對稱性,並不會改變拓樸性質,因此我們稱為這樣的相態是「對稱性保護的拓樸相態 (Symmetry protected topological phases) 」。
這就是拓樸相態的重要性。量子電腦需要用到量子訊息,可惜的是,量子訊息常常因為雜訊一下子就不見,因此我們如果要用到很多量子位元,保持量子訊息很重要。拓樸態,舉例來說,像是一個有洞的物質,而這些洞可以拿來作為量子位元。舉例來說,我們有一個麵團做的甜甜圈,我們的手可以去改變甜甜圈的形狀,但只要不把洞黏起來,或是打另一個洞,不管我們怎麼捏,一個洞還是保持在那。我們可以想像,雜訊就好像我們的手亂捏,會改變甜甜圈的樣子,但洞永遠在那,也就是拓樸性質永遠不變,這樣的拓樸材質非常適合來當做量子電腦的量子位元。
墊基於這三位物理學家的研究基礎,在最近的十多年,大量的拓樸物質在實驗上被製造與發現,比如說拓樸絕緣體(Topological Insulators),拓樸超導體(Topological superconductors), 和外爾半導體(Weyl Semimetal)。這些新的奇異拓樸物質的發現,大大延展人類可能的科技發展,增加量子電腦的可能性,因此獲頒諾貝爾物理學獎的殊榮。
本文摘自《物理雙月刊》38 卷 12 月號 ,更多文章請見物理雙月刊網站。