你知道心肺復甦術的存活率嗎？「叫叫 CAB」背後的數據——《醫學的張力》

• 作者／賴昭正｜前清大化學系教授、系主任、所長；合創科學月刊

我擔心人工智慧可能會完全取代人類。如果人們能設計電腦病毒，那麼就會有人設計出能夠自我改進和複製的人工智慧。 這將是一種超越人類的新生命形式。

——史蒂芬．霍金（Stephen Hawking）　英國理論物理學家

大約在八十年前，當第一台數位計算機出現時，一些電腦科學家便一直致力於讓機器具有像人類一樣的智慧；但七十年後，還是沒有機器能夠可靠地提供人類程度的語言或影像辨識功能。誰又想到「人工智慧」（Artificial Intelligent，簡稱 AI）的能力最近十年突然起飛，在許多（所有？）領域的測試中擊敗了人類，正在改變各個領域——包括假新聞的製造與散佈——的生態。

圖形處理單元（graphic process unit，簡稱 GPU）是這場「人工智慧」革命中的最大助手。它的興起使得九年前還是個小公司的 Nvidia（英偉達）股票從每股不到 $5，上升到今天（5 月 24 日）每股超過 $1000（註一）的全世界第三大公司，其創辦人（之一）兼首席執行官、出生於台南的黃仁勳（Jenson Huang）也一躍成為全世界排名 20 內的大富豪、台灣家喻戶曉的名人！可是多少人了解圖形處理單元是什麼嗎？到底是時勢造英雄，還是英雄造時勢？

在回答這問題之前，筆者得先聲明筆者不是學電腦的，因此在這裡所能談的只是與電腦設計細節無關的基本原理。筆者認為將原理轉成實用工具是專家的事，不是我們外行人需要了解的；但作為一位現在的知識分子或公民，了解基本原理則是必備的條件：例如了解「能量不滅定律」就可以不用仔細分析，即可判斷永動機是騙人的；又如現在可攜帶型冷氣機充斥市面上，它們不用往室外排廢熱氣，就可以提供屋內冷氣，讀者買嗎？

CPU 與 GPU

不管是大型電腦或個人電腦都需具有「中央處理單元」（central process unit，簡稱 CPU）。CPU 是電腦的「腦」，其電子電路負責處理所有軟體正確運作所需的所有任務，如算術、邏輯、控制、輸入和輸出操作等等。雖然早期的設計即可以讓一個指令同時做兩、三件不同的工作；但為了簡單化，我們在這裡所談的工作將只是執行算術和邏輯運算的工作（arithmetic and logic unit，簡稱 ALU），如將兩個數加在一起。在這一簡化的定義下，CPU 在任何一個時刻均只能執行一件工作而已。

在個人電腦剛出現只能用於一般事物的處理時，CPU 均能非常勝任地完成任務。但電腦圖形和動畫的出現帶來了第一批運算密集型工作負載後，CPU 開始顯示心有餘而力不足：例如電玩動畫需要應用程式處理數以萬計的像素（pixel），每個像素都有自己的顏色、光強度、和運動等, 使得 CPU 根本沒辦法在短時間內完成這些工作。於是出現了主機板上之「顯示插卡」來支援補助 CPU。

1999 年，英偉達將其一「具有集成變換、照明、三角形設定／裁剪、和透過應用程式從模型產生二維或三維影像的單晶片處理器」（註二）定位為「世界上第一款 GPU」，「GPU」這一名詞於焉誕生。不像 CPU，GPU 可以在同一個時刻執行許多算術和邏輯運算的工作，快速地完成圖形和動畫的變化。

依序計算和平行計算

一部電腦 CPU 如何計算 7×5+6/3 呢？因每一時刻只能做一件事，所以其步驟為：

• 計算 7×5；
• 計算 6/3；
• 將結果相加。

總共需要 3 個運算時間。但如果我們有兩個 CPU 呢？很多工作便可以同時（平行）進行：

• 同時計算 7×5 及 6/3；
• 將結果相加。

只需要 2 個運算時間,比單獨的 CPU 減少了一個。這看起來好像沒節省多少時間，但如果我們有 16 對 a×b 要相加呢？單獨的 CPU 需要 31 個運算的時間（16 個 × 的運算時間及 15 個 + 的運算時間），而有 16 個小 CPU 的 GPU 則只需要 5 個運算的時間（1 個 × 的運算時間及 4 個 + 的運算時間）！

現在就讓我們來看看為什麼稱 GPU 為「圖形」處理單元。圖一左圖《我愛科學》一書擺斜了，如何將它擺正成右圖呢？ 一句話：「將整個圖逆時針方向旋轉 θ 即可」。但因為左圖是由上百萬個像素點（座標 x, y）組成的，所以這句簡單的話可讓 CPU 忙得不亦樂乎了：每一點的座標都必須做如下的轉換

x’ = x cosθ + y sinθ

y’ = -x sinθ+ y cosθ

即每一點均需要做四個 × 及兩個 + 的運算！如果每一運算需要 10^-6 秒，那麼讓《我愛科學》一書做個簡單的角度旋轉，便需要 6 秒，這豈是電動玩具畫面變化所能接受的？

人類的許多發明都是基於需要的關係，因此電腦硬件設計家便開始思考：這些點轉換都是獨立的，為什麼我們不讓它們同時進行（平行運算，parallel processing）呢？於是專門用來處理「圖形」的處理單元出現了——就是我們現在所知的 GPU。如果一個 GPU 可以同時處理 10⁶ 運算，那上圖的轉換只需 10^-6 秒鐘！

GPU 的興起

GPU 可分成兩種：

• 整合式圖形「卡」（integrated graphics）是內建於 CPU 中的 GPU，所以不是插卡，它與 CPU 共享系統記憶體，沒有單獨的記憶體組來儲存圖形／視訊，主要用於大部分的個人電腦及筆記型電腦上；早期英特爾（Intel）因為不讓插卡 GPU 侵蝕主機的地盤，在這方面的研發佔領先的地位，約佔 68% 的市場。
• 獨立顯示卡（discrete graphics）有不與 CPU 共享的自己專用內存；由於與處理器晶片分離，它會消耗更多電量並產生大量熱量；然而，也正是因為有自己的記憶體來源和電源，它可以比整合式顯示卡提供更高的效能。

2007 年，英偉達發布了可以在獨立 GPU 上進行平行處理的軟體層後，科學家發現獨立 GPU 不但能夠快速處理圖形變化，在需要大量計算才能實現特定結果的任務上也非常有效，因此開啟了為計算密集型的實用題目編寫 GPU 程式的領域。如今獨立 GPU 的應用範圍已遠遠超出當初圖形處理，不但擴大到醫學影像和地震成像等之複雜圖像和影片編輯及視覺化，也應用於駕駛、導航、天氣預報、大資料庫分析、機器學習、人工智慧、加密貨幣挖礦、及分子動力學模擬（註三）等其它領域。獨立 GPU 已成為人工智慧生態系統中不可或缺的一部分，正在改變我們的生活方式及許多行業的遊戲規則。英特爾在這方面發展較遲，遠遠落在英偉達（80%）及超微半導體公司（Advance Micro Devices Inc.，19%，註四）之後，大約只有 1% 的市場。

事實上現在的中央處理單元也不再是真正的「單元」，而是如圖二可含有多個可以同時處理運算的核心（core）單元。GPU 犧牲大量快取和控制單元以獲得更多的處理核心，因此其核心功能不如 CPU 核心強大，但它們能同時高速執行大量相同的指令，在平行運算中發揮強大作用。現在電腦通常具有 2 到 64 個核心；GPU 則具有上千、甚至上萬的核心。

結論

我們一看到《我愛科學》這本書，不需要一點一點地從左上到右下慢慢掃描,即可瞬間知道它上面有書名、出版社等，也知道它擺斜了。這種「平行運作」的能力不僅限於視覺，它也延伸到其它感官和認知功能。例如筆者在清華大學授課時常犯的一個毛病是：嘴巴在講，腦筋思考已經不知往前跑了多少公里，常常為了追趕而越講越快，將不少學生拋到腦後！這不表示筆者聰明，因為研究人員發現我們的大腦具有同時處理和解釋大量感官輸入的能力。

人工智慧是一種讓電腦或機器能夠模擬人類智慧和解決問題能力的科技，因此必須如人腦一樣能同時並行地處理許多資料。學過矩陣（matrix）的讀者應該知道，如果用矩陣和向量（vector）表達，上面所談到之座標轉換將是非常簡潔的（註五）。而矩陣和向量計算正是機器學習（machine learning）演算法的基礎！也正是獨立圖形處理單元最強大的功能所在！因此我們可以了解為什麼 GPU 會成為人工智慧開發的基石：它們的架構就是充分利用並行處理，來快速執行多個操作，進行訓練電腦或機器以人腦之思考與學習的方式處理資料——稱為「深度學習」（deep learning）。

黃仁勳在 5 月 22 日的發布業績新聞上謂：「下一次工業革命已經開始了：企業界和各國正與英偉達合作，將價值數萬億美元的傳統資料中心轉變為加速運算及新型資料中心——人工智慧工廠——以生產新商品『人工智慧』。人工智慧將為每個產業帶來顯著的生產力提升，幫助企業降低成本和提高能源效率，同時擴大收入機會。」

附錄

人工智慧的實用例子：下面一段是微軟的「copilot」代書、谷歌的「translate」代譯之「one paragraph summary of GPU and AI」。讀完後，讀者是不是認為筆者該退休了？

GPU（圖形處理單元）和 AI（人工智慧）之間的協同作用徹底改變了高效能運算領域。GPU 具有平行處理能力，特別適合人工智慧和機器學習所需的複雜資料密集運算。這導致了影像和視訊處理等領域的重大進步，使自動駕駛和臉部辨識等技術變得更加高效和可靠。NVIDIA 開發的平行運算平台 CUDA 進一步提高了 GPU 的效率，使開發人員能夠透過將人工智慧問題分解為更小的、可管理的、可同時處理的任務來解決這些問題。這不僅加快了人工智慧研究的步伐，而且使其更具成本效益，因為 GPU 可以在很短的時間內執行與多個 CPU 相同的任務。隨著人工智慧的不斷發展，GPU 的角色可能會變得更加不可或缺，推動各產業的創新和新的可能性。大腦透過神經元網路實現這一目標，這些神經元網路可以獨立但有凝聚力地工作，使我們能夠執行複雜的任務，例如駕駛、導航、觀察交通信號、聽音樂並同時規劃我們的路線。此外，研究表明，與非人類動物相比，人類大腦具有更多平行通路，這表明我們的神經處理具有更高的複雜性。這個複雜的系統證明了我們認知功能的卓越適應性和效率。我們可以一邊和朋友聊天一邊走在街上，一邊聽音樂一邊做飯，或一邊聽講座一邊做筆記。人工智慧是模擬人類腦神經網路的科技，因此必須能同時並行地來處理許多資料。研究人員發現了人腦通訊網路具有一個在獼猴或小鼠中未觀察獨特特徵：透過多個並行路徑傳輸訊息,因此具有令人難以置信的多任務處理能力。

註解

（註一）當讀者看到此篇文章時，其股票已一股換十股，現在每一股約在 $100 左右。

（註二）組裝或升級過個人電腦的讀者或許還記得「英偉達精視 256」（GeForce 256）插卡吧?

（註三）筆者於 1984 年離開清華大學到 IBM 時，就是參加了被認為全世界使用電腦時間最多的量子化學家、IBM「院士（fellow）」Enrico Clementi 的團隊：因為當時英偉達還未有可以在 GPU 上進行平行處理的軟體層，我們只能自己寫軟體將 8 台中型電腦（非 IBM 品牌！）與一大型電腦連接來做平行運算，進行分子動力學模擬等的科學研究。如果晚生 30 年或許就不會那麼辛苦了?

（註四）補助個人電腦用的 GPU 品牌到 2000 年時只剩下兩大主導廠商：英偉達及 ATI（Array Technology Inc.）。後者是出生於香港之四位中國人於 1985 年在加拿大安大略省成立，2006 年被超微半導體公司收購，品牌於 2010 年被淘汰。超微半導體公司於 2014 年 10 月提升台南出生之蘇姿豐（Lisa Tzwu-Fang Su）博士為執行長後，股票從每股 $4 左右，上升到今天每股超過 $160，其市值已經是英特爾的兩倍，完全擺脫了在後者陰影下求生存的小眾玩家角色，正在挑戰英偉達的 GPU 市場。順便一題：超微半導體公司現任總裁（兼 AI 策略負責人）為出生於台北的彭明博（Victor Peng）；與黃仁勳及蘇姿豐一樣，也是小時候就隨父母親移居到美國。

（註五）或。

延伸閱讀

• 「熱力學與能源利用」，《科學月刊》，1982 年 3 月號；收集於《我愛科學》（華騰文化有限公司，2017 年 12 月出版），轉載於「嘉義市政府全球資訊網」。
• 「網路安全技術與比特幣」，《科學月刊》，2020 年 11 月號；轉載於「善科教育基金會」的《科技大補帖》專欄。

於平均水溫 7°C 的 12 月底，一名 56 歲的男子，潛入瑞士日內瓦湖。肥胖的軀體（BMI = 33 kg/m²），緊繃著潛水衣，背上扛負沉重的開放式水肺。有 6 個月潛水經驗的他，在水中悠游無阻。10 分鐘後，來到水面下 19.5 公尺。^[1]

突然，他咳嗽且呼吸困難，但嘴裡仍含著潛水用的呼吸調節器。同行的人陪他，一起遵循減壓程序：^[1]每向上一段距離，就稍作停留，再繼續移動。^[2]3 分鐘後，他們回到水面，男子立刻吐血。緊接著在船上，他心臟病發，失去意識，被及時施予包含心肺復甦術（cardiopulmonary resuscitation，簡稱 CPR）在內的基本救命術（basic life support），長達 5 分鐘。直到船隻靠岸，改由急救團隊接手，執行高級心臟救命術（advanced cardiac life support）：除了 CPR，還做氣管插管（intubation）。期間血沫從他的口咽滲出。^[1]

在持續不斷的心肺復甦術下，男子被直升機送抵附近唯一設有高壓氧氣艙（hyperbaric oxygen chamber）的日內瓦大學醫院。進入急診室時，離急救開始，已經過了 84 分鐘。他呼吸著低流量的氧氣，情況依然不見好轉。時而心臟暫停跳動；時而心室頻繁顫抖。血液中乳酸含量飆高，pH 值下降。入院 20 分鐘，也就是展開 CPR 後的第 104 分鐘，男子被宣告死亡。^[1]

死因與責任歸屬

他的死因與相關責任的歸屬，得從 3 個面向的線索來分析：

1. 醫療紀錄：咳嗽、咳血、血沫，還有愈往水面愈惡化的病況等。之前的事件描述，大致涵蓋了重要資訊。^[1]
2. 警方調查：水溫、證人筆錄、潛水紀錄，以及潛水用具的運作狀況。警方排除潛水用具異常致死的可能。^[1]
3. 驗屍報告：屍體解剖、電腦斷層掃描、病理現象分析、尋找溺水跡象，以及組織學和毒物學檢驗等。驗屍在男子死後的隔天進行。他肺泡與肺泡之間的肺間質（pulmonary interstitium），病變增厚；^[1]肺泡破裂出血，形成肺氣腫（pulmonary emphysema），且淤積液體；^{[1, 3]}部份肺臟被填滿，呈現肺實變（pulmonary consolidations）。另外，呼吸道有少量泡沫和血液；心臟肥大；而且因為肥胖的緣故，肺動脈及冠狀動脈有脂肪斑紋（fatty streaks）。不過整體而言，沒有任何溺水的跡象。^[1]

浸入性肺水腫

最後男子的死因，被判定為浸入性肺水腫（immersion pulmonary oedema）。《國際法醫期刊》（International Journal of Legal Medicine）的論文，分析此症詳細的形成機制，有下列幾種可能：^[1]

1. 人在水中的時候，水壓會促進心肺氣體交換的血液循環，也就是肺循環，以及提升心臟的血液輸出量，即心輸出量。因此而集中的血液，帶來過大的壓力，令肺部的微血管不堪負荷，血液便滲入肺泡。此時，其他因素也可能惡化病況，例如：緊繃的潛水衣、冰水收縮血管、高血壓、心臟肥大、體內水份過多、心理壓力和劇烈運動等。^[1]
2. 水壓集中血液，增加了右心室的工作量，使得左右兩個心室的輸出失衡，也造成肺部微血管壓力衰竭，終致水腫。如果病患原本還有左心室或心臟瓣膜異常，問題會更嚴重。^[1]
3. 水壓升高肺部的血壓，以及從潛水氣瓶費勁吸氣，都可能危及肺泡與肺部微血管；而呼吸不順的心理壓力、運動大量換氣，還有不當使用呼吸調節器的氣流阻力等，則加重對肺部微血管的傷害。^[1]

急救和治療

一般潛水者察覺身體不適，當下會想回到水面上。然而，在水中上升的過程裡，逐步減壓的身體，會產生下列變化：無法繼續溶於血液的氣體被釋出，氣泡於是傷害肺部微血管；胸腔裡的氣體膨脹，水腫重新分佈；肺泡內壓力下降，拉大肺泡與肺部微血管的壓力梯度。這些都會使浸入性肺水腫的症狀惡化。^[1]

儘管如此，急救的第一個動作，還是得把病患盡快送至水面。^[1]情況許可的話，才在不同的水深處暫時停留，使氣體能安全地從身體組織釋出，免於氣泡的產生。^[2]遠離水壓，脫去潛水衣，並溫暖身體，以減少血液過度向心肺集中。如果沒有生命危險，就讓病患坐下，經由面罩吸入高濃度的氧氣，然後送去有加護病房和高壓氧氣艙的醫院。^[1]

在醫院裡，無論是用侵入性或非侵入性的呼吸器，都要以正壓維持呼吸道通暢。除非併發減壓疾病，系統性的高壓氧氣治療，其實沒有必要。^[1]同時，醫師可能也會開 β2-交感神經促進劑（beta-2 agonists），這種常見的氣管擴張藥物，加速肺泡清除液體。^{[1, 4]}至於心臟的部份，硝化甘油（nitroglycerin）點滴則能放鬆血管，調節左右心室的血液流量。^{[1, 5]}

多數浸入性肺水腫的案例，不像此男子這麼嚴重，大約 2 至 3 天即可出院。不過，1 個月內，絕對不得再潛水或游泳。最好由醫師診斷，是否罹患高血壓、糖尿病、高血脂等心血管疾病，並檢查呼吸功能有無異常。未來下水時，務必選擇水溫暖和的地點，穿著合身的潛水衣，限制活動的水深與時間長度，還要避免水份過量，或吸入太多氧氣。^[1]

參考資料

1. Evain F, Louge P, Pignel R, et al. (2022) ‘Fatal diving: could it be an immersion pulmonary edema? Case report’. International Journal of Legal Medicine, 136, 713–717.
2. ‘CHAPTER 3 — Underwater Physiology and Diving Disorders’. (2016) In: U.S. Navy Diving Manual — Volume 1. U.S. (pp. 50) Naval Sea Systems Command.
3. ‘Emphysema’. (28 APR 2017) Mayo Clinic.
4. Hsu E, Bajaj T. (23 JUN 2022) ‘Beta 2 Agonists’. In: StatPearls. Treasure Island (FL): StatPearls Publishing.
5. Kim KH, Kerndt CC, Adnan G, et al. (27 SEP 2022) ‘Nitroglycerin’. In: StatPearls. Treasure Island (FL): StatPearls Publishing.

• 作者：蘇上豪

在一九七四年六月下旬的《西雅圖時報》（The Seattle Times），出現了一則相當吸引人的新聞，一位退休的餐廳老闆，以薩克．皮哈（Isaac Piha）在家族聚餐的地點，救活了一位差點被噎死的婦人。

當時是星期天的下午，皮哈一家人正在餐廳包廂內慶祝父親節，忽然鄰近的客人愛德華．伯加徹斯（Edward Bagachus）前來求救，原來他的老婆艾琳（Irene）沒有辦法呼吸，於是皮哈帶著自己的兩個兒子前去幫忙。

皮哈發現艾琳癱軟在餐桌上，臉色鐵青無法呼吸，第一眼瞥見她時，皮哈原本以為是艾琳心臟病發作，但隨後看到桌子上的食物，他立刻了解應該是食物造成她無法呼吸。

於是皮哈依照最近學到的方法，從艾琳的背後環抱，用力在她的腹部擠壓，接著一片雞肉「啵」一聲從她嘴巴彈了出來，沒有多久，艾琳恢復呼吸，從鬼門關內被拉了回來，這是歷史上第一次利用「哈姆立克（Heimlich Maneuver）急救法」成功救回患者的案例。

以當今的眼光來看，這並不是什麼神奇的事情，因為我們從任何一個民間機構辦理的急救訓練裡，都會學到相同的救人招式，但是對於一九七○年代的皮哈來說，這個急救方法不要說是起步，它還只是報紙專欄中，記者剛剛分享的一則評論。

讀者們聽起來可能會覺得是天方夜譚，但事實的確是如此。記者詢問了皮哈為何對此急救法的報導有興趣，甚至學了起來，他的回答更是關鍵，因為從事餐飲業多年，看過不少顧客因為食物卡在喉嚨而一命歸西，自然看到報紙上「哈姆立克急救法」的介紹有所感悟，沒有想到學起來之後真的派上用場，救活了身邊瀕臨死亡的人。

對於我如此輕鬆介紹風行迄今超過四十年的「哈姆立克急救法」，讀者可能有些困惑，一個如此重要的方法，竟然是由升斗小民搶先完成，但從它發明的背景來看，你就不得不佩服發明人亨利．哈姆立克（Henry Heimlich）的真知灼見，要不是他簡化流程及利用大眾媒體的力量宣傳，讓此急救法能快速被人們接受，不知道它還要拖到什麼時候可以救人。

「壓迫腹部」的急救方法

至於哈姆立克為何會發明此一簡便的急救方式，拯救被食物噎到無法呼吸的病人呢？這又要從他的專業背景以及看到的一則報導談起。

一九四三年畢業於康乃爾大學醫學院的哈姆立克是位胸腔外科醫師，同時也是研究吞嚥問題的專家。一九七二年一篇《紐約時報雜誌》（The New York TimesMagazine）的報導，吸引了他的注意，內文談到的是美國人因為進食時被噎死的意外。

根據當時所揭露的資料顯示，光是美國一年被食物噎死的民眾就有三千人之多，此原因還盤踞在意外死亡的第六位，這對一位成天在醫院的白色巨塔裡處理病人吞嚥的醫師而言，實在難以置信。

於是哈姆立克醫師開始蒐集資料，才發現事情的嚴重性超乎他的想像。除了上述報導的真實性無誤外，有不少名人也是被食物噎死的冤魂，例如羅伯特．甘迺迪（Robert F. Kennedy）的老婆埃賽爾．甘迺迪（Ethel Kennedy），知名樂手湯米．多西（Tommy Dorsey）、卡斯．艾略特（Cass Elliot），甚至羅馬皇帝克迪斯一世（ClaudiusI）等，都是因為同一原因命喪黃泉。

醫師的天性讓哈姆立克想到要好好研究此一問題，於是他開始研究當時的急救法是如何處理這個問題，他發現紅十字會（當時傳播急救方法最重要的民間組織）教的是努力拍打患者的背部，希望他能將噎在喉嚨的食物可以順利吞下；另外有人使出更激烈的手段，如用手去喉嚨硬挖，或是讓病人頭低腳高，只是哈姆立克發現這些方法並沒有科學論述的根據，完全是依照不知哪位醫師的憑空想像，以至於以訛傳訛，不知其所以然沿用著。

想要撥亂反正的哈姆立克開始利用動物實驗找出解決的方案。他在隔年以塞住的氣管內管，放到被麻醉的小獵犬咽喉裡模擬食物噎住的狀況。由於當時體外心臟按摩術正如火如荼應用於急救上，於是他用壓迫胸廓的方法嘗試，看看是否能把塞入的管子從小狗身上彈出，可惜結果徒勞無功，因此他靈機一動，以手壓迫腹部，發現管子很輕易地彈了出來。

在動物實驗得到成果的哈姆立克，把腦筋動到人的身上。於是找了醫院十位同事，每位嘴上含著流量計，然後藉由壓迫腹部來評估氣流的大小，結果發現力量竟然可以達到每分鐘二百零五公升（205 Liters/min），據此哈姆立克已經找到急救食物噎住病人的可靠方法，他認為壓迫腹部將食物彈出是「快速而且便利」。

大眾媒體使急救法迅速普及

哈姆立克為了讓上述方法操作更簡便，將它分成自救，從背後環抱及倒地患者的處置，用十分容易上手的模式，希望讓所有的人可以很快學會，只是在考慮公布它的方式時，他做了不一樣的決定，他不想在主流醫學期刊公布，反而找上了一個半專業的《急診醫學》（Emergency Medicine）雜誌。

除了和主編熟稔之外，哈姆立克想到的是希望可以將此急救方法快速傳播到每個角落，因為專業的醫學期刊限制很多，雖然刊登之後可以累積聲望，但離臨床應用可能拖上一年半載，在《急診醫學》刊出不只專業人士可以接觸，一般普羅大眾也能學習。

另外他也找了幾位認識的記者朋友，從《芝加哥每日新聞》（Chicago DailyNews）、《西雅圖時報》等等，在報紙的專欄裡教導民眾如此簡便的急救方法，而他說服這些記者的理由很簡單，現今的醫療無法解決這樣的急症，試一試新的方也未嘗不可。當然，他也費心提供自己動物與人體實驗的證據，只是這些沒有刊在報紙上。

所以在皮哈第一次利用「哈姆立克急救法」的前一個禮拜，美國幾個主流報紙專欄已經出現了前述的方法，而且不到兩個月的時間，有不少被食物噎住的民眾因此被身邊的人救活。

不到兩個月，在一九七四年八月，《美國醫學會雜誌》（The Journal of AmericanMedical Association，簡稱JAMA）介紹了此方法，並且將它訂名為「哈姆立克急救法」，以表彰哈姆立克費心的推廣以及救人的貢獻！

如同哈姆立克的判斷，美國的衛生部遲至一九八五年才將「哈姆立克急救法」列為官方認可，可以搶救遭食物噎住病患的方式，同時紅十字會及美國心臟協會才跟進，離它第一次問世已經超過十年，它會受到青睞的重要原因，是普羅大眾已經用此方法救活身邊數不清瀕臨噎死的病人。

相信之後的演變並不需要我再多言，有參加過急救訓練的讀者一定體驗過此方法，雖然目前有稍作修正，但仍無損於哈姆立克醫師的貢獻。故事到這邊結束了嗎？其實還沒有，二○一六年十二月逝世的哈姆立克，在同年五月入住辛辛那提的一家老人療養院時，九十六歲的他還親自用此技術救了一位八十七歲老太太。

看到「哈姆立克急救法」流行的推手是大眾媒體，的確讓我感觸很多。在一九七○年代的美國身為媒體的責任是如此被重視，反觀今日的台灣，卻仍是令人汗顏，醫療節目合併在烹飪節目中，不只傳播似是而非的觀念，還讓沒有專業醫療背景的人解釋病症及治療方式，而身為醫師的我卻無能為力，真希望自己像哈姆立克醫師一樣，可以認識更多的主流媒體傳播正確的觀念才是。

——本文摘自《怪奇醫療史：從疫苗發明、疾病歷史、護體神功、縮陽症、按摩槍等，解開最不可思議的醫學古今事》，2022 年 10 月，時報出版出版，未經同意請勿轉載。

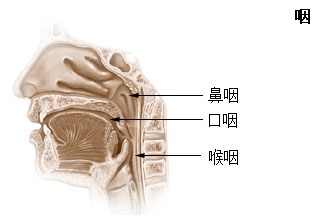
• 作者 / 哈利・柯林斯，崔佛・平區（Harry Collins, Trevor Pinch）
• 譯者 / 李尚仁

評估存活率不是一件容易的事情

直到今天，美國還未全面得知心肺復甦術的存活率。沒有全國性的資料庫，醫學研究者和政策制定者沒辦法知道有多少人接受過心肺復甦術。研究者必須仰賴短期小規模研究所估算的區域存活率。這類數字通常會有很大的差異。

有個研究比較美國二十九個城市從一九六七年到一九八八年之間接受心肺復甦術後的存活率，發現其差距從愛荷華州的百分之二到華盛頓州金恩郡的百分之二十六。

整體而言，這些存活率和一九七三年的樂觀形成強烈對比。這些研究也確認此時心肺復甦術已建立其普及度，一般大眾學習心肺復甦術，在好幾個社區有一半以上的復甦是由路人主動進行的。此外，大多數的緊急醫療體系已經成功改組。

為何存活率有差異？

研究者開始擔心究竟是什麼因素，導致存活率出現這樣的差異？愛荷華州百分之二的存活率，意味著每五十次的復甦努力只有一次會成功；而西雅圖則平均每四次努力就有一次可以救活對方。然而，要了解這些數字的意義，西雅圖和愛荷華州的復甦術存活率必須用相同的基準線來計算。

就以反應時間（response time）這個已知會影響存活率的變數為例。這是從昏倒和開始進行復甦術之間的時間。然而，文獻對於「反應時間」沒有清楚的定義。正如米基．艾森保醫師（Dr. Mickey Eisenberg）在回顧文獻時所注意到，它可能包含以下所有或部分的動作：辨識、決定打電話求救、打電話、派遣中心問話、進行派遣、從急救站趕到現場、從現場趕到病人身邊（Eisenberg ，引自Timmermans，70）。

除了反應時間之外，艾森保也發現「心臟停止」、「路人實施心肺復甦術」、「旁人注意到心臟停止」、「心室顫動」以及「入院」等基本名詞的定義分歧。就有效的比較而言，更重要的是，研究者對復甦與存活（survival）這兩個存活率的關鍵要素有不同的定義。

有些人把任何進行心肺復甦術的嘗試，都界定為復甦的努力，其他人則將此侷限於特定的心律問題，像是心室性心搏過速（ventricular tachycardia）。

「存活」也是含糊的字眼。在某些研究中，它意味著出院時只有很輕微的神經學損傷；其他研究指的則是在進加護病房時還有能夠生存的脈搏。如果還加上各區域醫療系統之間必然會有的差異，那顯然要詮釋存活率就更加困難了。

量化心肺復甦的效果前，先統一標準吧！

為了要克服這個無所不在的定義問題，一九九○年在挪威外海小島上的烏特斯坦修道院舉行了烏特斯坦共識會議（Utstein Consensus Conference），將定義予以標準化，並且提出一套統一的存活率計算公式。

新的公式是「分母是因心臟病導致心室震顫而停止心跳的人數，分子是〔從醫院〕出院還活著的〔病〕人數」（Timmermans，73）。換句話說，患者必須先前就已經有心臟的毛病，而不是由溺水或電擊等其他事件所引起的。

此一存活率定義遠比之前所使用的定義狹隘。它排除了許多的事件和意外（包括溺水），而這些在過去兩世紀都被視為是復甦術的適用範圍。此外它也排除了未被人見證到的心跳停止，以及不是由旁觀者實施第一次心肺復甦術的病人。由於這個定義只含括那些生存機會最佳的案例，因此相較於使用更為廣泛定義的研究，其估算出來的生存率會膨脹很多。

事實上，會用到心肺復甦術的大多數狀況（占所有案例的百分之六十到八十），現在都排除在統計數字之外。另一方面，出院時還活著的病人都列入計算，這樣的標準所創造出來的存活率則相對地高，儘管美國各醫院乃至全世界醫院的出院標準並不一致。

最終效果仍不樂觀

自一九九一年以來，有一些研究是根據烏特斯坦的標準來進行的。雖然選擇了最健康也最均質的樣本，存活率仍舊低得讓人失望，而且還是有很大的差異。

例如一個在芝加哥進行的研究發現，非裔美國人的存活率是百分之零點八，而白人的存活率則是百分之二點六。此一研究結果的論文標題相當適切：〈大都會地區心肺復甦術的結果──存活者在哪裡呢？〉紐約市的存活率很低，只有百分之一點四。

另一方面，密西根州奧克蘭郡則有百分之十四點九的存活率。正如提摩曼斯所指出（74），醫學文獻總是對數字做樂觀的詮釋。低存活率被歸咎於大都會地區醫療服務的品質不良。心肺復甦術的支持者論稱，只要有更成熟的急救體系和必要的政治意志，任何地方都應該能夠達到西雅圖那般高達百分之三十的存活率。

及早進行除顫被視為是改善存活率的關鍵，有些研究指出百分之八十到九十的存活者曾經接受過心室顫動的治療，而這不是路人在沒有他人協助下所能擁有的技術。美國目前所採取的策略是提升除顫器的普及性，以至於它們現在就像滅火器一樣，是飛機、健身房、辦公室等地方的標準配備。

有除顫的存活率數字要比其他的統計數字稍微好一點；然而區域之間還是有差異，而且很少有令人信服的證據顯示存活率出現了突破。

也許提摩曼斯提出了一個關於統計數字的深刻論點。他認為由於醫療社群和一般大眾對於心肺復甦術的信念投入很多，因此不管統計數字多低，都無法損及認定它有效的觀念。

存活率不佳被解釋為意味著緊急醫療服務和醫療基礎建設還需要改良，才能得到更好的存活率。至於心肺復甦術的有效性以及必要性則很少受到質疑。

即便強力支持心肺復甦術的美國心臟協會在一九九一年也承認，出現心跳停止之後的人，能夠活著出院的比例不過百分之一到百分之三，而且由於資料品質不良，真正的百分比「或許更低」（Timmermans，4）。

——本文摘自《醫學的張力》，2021 年 9 月，左岸文化。