一點都不放過！家電廢熱可以回收再發電!?

本文與財團法人臺灣生活美學基金會合作。 

AI 有可能造成人們失業嗎？還是 AI 會成為個人專屬的超級助理？

隨著人工智慧技術的快速發展，AI 與人類之間的關係，成為社會大眾目前最熱烈討論的話題之一，究竟，AI 會成為人類的取代者或是協作者？決定關鍵就在於人們對 AI 的了解和運用能力，唯有人們清楚了解如何使用 AI，才能化 AI 為助力，提高自身的工作效率與生活品質。

有鑑於此，目前正於臺灣當代文化實驗場 C-LAB 展出的「2024 未來媒體藝術節」，特別將展覽主題定調為奇異點（Singularity），透過多重視角探討人工智慧與人類的共生關係。

C-LAB 策展人吳達坤進一步說明，本次展覽規劃了 4 大章節，共集結來自 9 個國家 23 組藝術家團隊的 26 件作品，帶領觀眾從了解 AI 發展歷史開始，到欣賞各種結合科技的藝術創作，再到與藝術一同探索 AI 未來發展，希望觀眾能從中感受科技如何重塑藝術的創造範式，進而更清楚未來該如何與科技共生與共創。

從歷史看未來：AI 技術發展的 3 個高峰

其中，展覽第一章「流動的錨點」邀請了自牧文化 2 名研究者李佳霖和蔡侑霖，從軟體與演算法發展、硬體發展與世界史、文化與藝術三條軸線，平行梳理 AI 技術發展過程。

藉由李佳霖和蔡侑霖長達近半年的調查研究，觀眾對 AI 發展有了清楚的輪廓。自 1956 年達特茅斯會議提出「人工智慧（Artificial Intelligence））」一詞，並明確定出 AI 的任務，例如：自然語言處理、神經網路、計算學理論、隨機性與創造性等，就開啟了全球 AI 研究浪潮，至今將近 70 年的過程間，共迎來三波發展高峰。

第一波技術爆發期確立了自然語言與機器語言的轉換機制，科學家將任務文字化、建立推理規則，再換成機器語言讓機器執行，然而受到演算法及硬體資源限制，使得 AI 只能解決小問題，也因此進入了第一次發展寒冬。

之後隨著專家系統的興起，讓 AI 突破技術瓶頸，進入第二次發展高峰期。專家系統是由邏輯推理系統、資料庫、操作介面三者共載而成，由於部份應用領域的邏輯推理方式是相似的，因此只要搭載不同資料庫，就能解決各種問題，克服過去規則設定無窮盡的挑戰。此外，機器學習、類神經網路等技術也在同一時期誕生，雖然是 AI 技術上的一大創新突破，但最終同樣受到硬體限制、技術成熟度等因素影響，導致 AI 再次進入發展寒冬。

走出第二次寒冬的關鍵在於，IBM 超級電腦深藍（Deep Blue）戰勝了西洋棋世界冠軍 Garry Kasparov，加上美國學者 Geoffrey Hinton 推出了新的類神經網路算法，並使用 GPU 進行模型訓練，不只奠定了 NVIDIA 在 AI 中的地位， 自此之後的 AI 研究也大多聚焦在類神經網路上，不斷的追求創新和突破。

從現在看未來：AI 不僅是工具，也是創作者

隨著時間軸繼續向前推進，如今的 AI 技術不僅深植於類神經網路應用中，更在藝術、創意和日常生活中發揮重要作用，而「2024 未來媒體藝術節」第二章「創造力的轉變」及第三章「創作者的洞見」，便邀請各國藝術家展出運用 AI 與科技的作品。

例如，超現代映畫展出的作品《無限共作 3.0》，乃是由來自創意科技、建築師、動畫與互動媒體等不同領域的藝術家，運用 AI 和新科技共同創作的作品。「人們來到此展區，就像走進一間新科技的實驗室，」吳達坤形容，觀眾在此不僅是被動的觀察者，更是主動的參與者，可以親身感受創作方式的轉移，以及 AI 如何幫助藝術家創作。

而第四章「未完的篇章」則邀請觀眾一起思考未來與 AI 共生的方式。臺灣新媒體創作團隊貳進 2ENTER 展出的作品《虛擬尋根-臺灣》，將 AI 人物化，採用與 AI 對話記錄的方法，探討網路發展的歷史和哲學，並專注於臺灣和全球兩個場景。又如國際非營利創作組織戰略技術展出的作品《無時無刻，無所不在》，則是一套協助青少年數位排毒、數位識毒的方法論，使其更清楚在面對網路資訊時，該如何識別何者為真何者為假，更自信地穿梭在數位世界裡。

透過歷史解析引起共鳴

在「2024 未來媒體藝術節」規劃的 4 大章節裡，第一章回顧 AI 發展史的內容設計，可說是臺灣近年來科技或 AI 相關展覽的一大創舉。

過去，這些展覽多半以藝術家的創作為展出重點，很少看到結合 AI 發展歷程、大眾文明演變及流行文化三大領域的展出內容，但李佳霖和蔡侑霖從大量資料中篩選出重點內容並儘可能完整呈現，讓「2024 未來媒體藝術節」觀眾可以清楚 AI 技術於不同階段的演進變化，及各發展階段背後的全球政治經濟與文化狀態，才能在接下來欣賞展區其他藝術創作時有更多共鳴。

「畢竟展區空間有限，而科技發展史的資訊量又很龐大，在評估哪些事件適合放入展區時，我們常常在心中上演拉鋸戰，」李佳霖笑著分享進行史料研究時的心路歷程。除了從技術的重要性及代表性去評估應該呈現哪些事件，還要兼顧詞條不能太長、資料量不能太多、確保內容正確性及讓觀眾有感等原則，「不過，歷史事件與展覽主題的關聯性，還是最主要的決定因素，」蔡侑霖補充指出。

舉例來說，Google 旗下人工智慧實驗室（DeepMind）開發出的 AI 軟體「AlphaFold」，可以準確預測蛋白質的 3D 立體結構，解決科學家長達 50 年都無法突破的難題，雖然是製藥或疾病學領域相當大的技術突破，但因為與本次展覽主題的關聯性較低，故最終沒有列入此次展出內容中。

除了內容篩選外，在呈現方式上，2位研究者也儘量使用淺顯易懂的方式來呈現某些較為深奧難懂的技術內容，蔡侑霖舉例說明，像某些比較艱深的 AI 概念，便改以視覺化的方式來呈現，為此上網搜尋很多與 AI 相關的影片或圖解內容，從中找尋靈感，最後製作成簡單易懂的動畫，希望幫助觀眾輕鬆快速的理解新科技。

吳達坤最後指出，「2024 未來媒體藝術節」除了展出藝術創作，也跟上國際展會發展趨勢，於展覽期間規劃共 10 幾場不同形式的活動，包括藝術家座談、講座、工作坊及專家導覽，例如：由策展人與專家進行現場導覽、邀請臺灣 AI 實驗室創辦人杜奕瑾以「人工智慧與未來藝術」為題舉辦講座，希望透過帶狀活動創造更多話題，也讓展覽效益不斷發酵，讓更多觀眾都能前來體驗由 AI 驅動的未來創新世界，展望 AI 在藝術與生活中的無限潛力。

展覽資訊：「未來媒體藝術節——奇異點」2024 Future Media FEST-Singularity 
展期 ▎2024.10.04 ( Fri. ) – 12.15 ( Sun. ) 週二至週日12:00-19:00，週一休館
地點 ▎臺灣當代文化實驗場圖書館展演空間、北草坪、聯合餐廳展演空間、通信分隊展演空間
指導單位 ▎文化部
主辦單位 ▎臺灣當代文化實驗場

本文轉載自諾貝爾化學獎專題系列，原文為《【2011諾貝爾化學獎】具有黃金比例的晶體 — 準晶》

• 譯者／蔡蘊明｜台大化學系名譽教授
• 圖／曹一允｜美國德州農工大學 Karen Wooley 教授指導下取得博士，現於日本萊雅公司進行研究。

十重對稱的黃金比例

當丹尼．謝西曼（Daniel Shechtman）將這個讓他得到 2011 年諾貝爾化學獎的發現登記於實驗記錄簿上時，在後面寫下了三個問號，因為從那些在他眼前的晶體裡面的原子，產生了一個不可能的對稱性，那就好像一個足球——一個球面 ——不可能只由正六邊形組成。從此之後，有趣的馬賽克圖案（Mosaic）、數學裡面的黃金比例以及藝術，幫科學家們解釋了謝西曼那令人困惑的觀察。

「Eyn chaya kazoo」，丹尼．謝西曼用希伯來語告訴自己「不可能有這種東西」。時值 1982 年 4 月 8 號的早晨，他正在研究的物質，是一個由鋁和錳組成的混合物，看起來很奇怪，因此他用電子顯微鏡，企圖從原子的層次來觀察，但是透過電子顯微鏡得到的圖像，卻違反了所有的邏輯：他看到一些同心圓，每一個都是由十個相互等距的亮點所組成（圖 1）。

謝西曼迅速地將灼熱的熔化金屬冷卻下來。這種溫度的突然改變應該會讓原子的排列混亂，但是他所觀察到的圖案，卻說出了一個完全不同的故事：那些原子以一種違反自然定律的方式而排列。謝西曼一再重複地數著那些點，四個或六個點是可能的，但十個是絕不可能。他在實驗記錄簿上寫下：十重對稱？？？

一個未知的發現

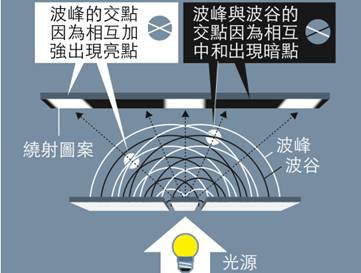
為了瞭解謝西曼的實驗結果，以及為何他會如此驚訝，讓我們想像下面的一個課堂實驗：一位物理老師讓光通過一個鑿有縫隙的金屬板，一個被稱為繞射光柵的物體（圖 2），當光波通過這個光柵時，它會產生折射，就好像海浪的波紋通過一個防波堤的開口一般。

在光柵的另一邊，波紋以一個半圓方式散開，並與其它的波紋相交，波峰與波谷相互地加強或減弱。在繞射光柵後面的螢幕上，一種具有明暗的紋路出現，稱為繞射圖紋。

這就是謝西曼在 1982 年 4 月早晨所得到的那種繞射圖紋（圖 1），只不過他的實驗是不同的：他不是用光，而是用電子（註：電子具有波的性質），而他的光柵就是那個快速冷卻了的金屬原子之間的縫隙。

此外，他的實驗是三度空間的，而非平面的。

那個繞射圖紋顯示，在那金屬之內的原子是排列成一個整齊有序的晶體。這當然不意外，幾乎所有的固體物質，不論是冰塊或金子，都具有整齊的晶體。雖然謝西曼使用電子顯微鏡非常有經驗，然而，一個由十個亮點排列成的圓形，卻是過去他從未看到過的。

更有甚者，這樣的晶體並沒有被列在國際晶體規格表之內，那是一個結晶學的主要參考指引。在當時的科學，明訂了一個由十個亮點排列成的圓形圖紋是不可能的，而其證明是非常簡單而明顯的。

違反所有邏輯的圖紋

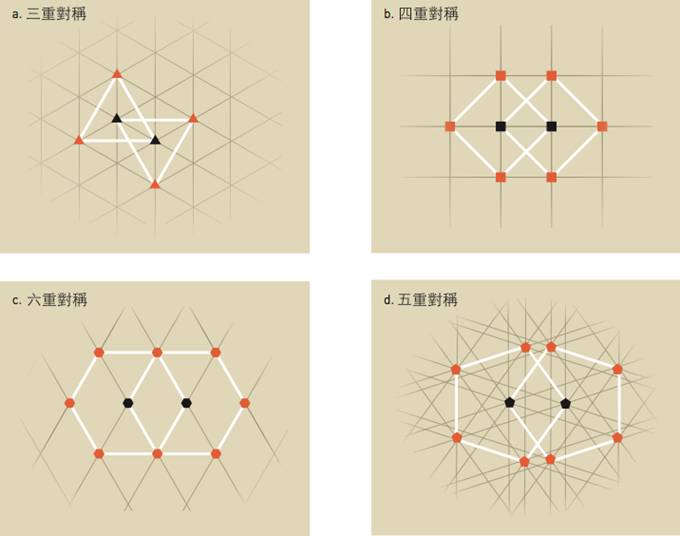
在一個晶體中，原子是以固定而重複的方式排列的。決定於化學的組成，它們會具有不同的對稱性。在圖 3a 中，我們可以看到每一個原子是由三個原子圍繞著，而形成不斷重複的排列圖案，產生一個三重對稱；將此圖案轉動 120 度，又會得到相同的圖案。

同樣的原理發生在四重對稱（圖 3b）以及六重對稱（圖 3c），圖案不斷重複。當你個別地轉動 90 度或 60 度，相同的圖案會重複出現。

然而，五重對稱（圖 3d）是不可能的，某些原子之間的距離會小於其它原子之間的距離，也就是說，相同的圖案不會重複。科學家認為這足以證明五重對稱不可能存在於晶體中。同樣的原因存在於七重對稱或更高重的對稱。

謝西曼卻發現，他的圖案轉動一個圓的十分之一的角度（36 度）時，又可得到相同的圖案。他的確看到了一個被認為不可能的十重對稱，因此，不意外地，他在實驗記錄簿上寫下了三個問號。

基本假設出錯了

在美國國家標準局（NIST），謝西曼從他的辦公室向外探頭，望了望走廊，希望能看到某一個可以與他分享發現的人，但是走廊空無一人，所以他回到電子顯微鏡前，對那個晶體繼續進一步的實驗。其中他重複地確認所得到的不是巒晶（twin crystal）：兩種共生的晶體享有相同的晶面，而導致了奇怪的繞射圖紋；但是他無法找到任何的跡象顯示那是巒晶。

除此之外，他將電子顯微鏡下的晶體轉動，看看到底要轉多少度可以讓這個十重對稱的繞射圖紋重複出現。實驗顯示晶體的對稱性與圖紋的十重對稱不同，但仍然是一個不可能的五重對稱。謝西曼的結論是：科學界的基本假設是錯誤的。

當謝西曼告訴科學家們他的發現時，他面對了完全的否定，一些同事們甚至認為這根本是無稽之談，許多人宣稱他所得到的是巒晶。實驗室的主管丟給了他一本結晶學教科書，建議他讀讀。謝西曼當然知道教科書裡面說了什麼，但是他更相信自己的實驗。

根據謝西曼的回憶，所有的騷動終於導致他的老闆要求他離開那個研究小組，狀況變得非常難堪。

與已知奮戰

謝西曼是在以色列科技大學（Technion-Israel Institute of Technology）修得博士學位的。在 1983 年，他引發了在他母校任職的伊蘭．布雷契（Ilan Blech）對這個研究的興趣，他們合力企圖解釋此一繞射圖紋，並轉譯成為原子在晶體內的排列模式。

於 1984 年夏，他們送了一份論文稿到應用物理期刊（Journal of Applied Physics），但是該稿似乎在收到當日，就即刻被編輯退回。

接著，謝西曼向約翰．康（John Cahn）提出要求。康是一位著名的物理學家，也是當初邀聘謝西曼到 NIST 的人。謝西曼希望康能看看他的數據。這位通常很忙的學者終於答應，接著，康與一位法國的結晶學家丹尼斯．格拉提亞斯（Denis Gratias）諮詢，看看謝西曼是否忽略了什麼，但是根據格拉提亞斯的檢驗，謝西曼的實驗是可以信賴的，格拉提亞斯如果親自做那些實驗，也會使用同樣的方法。

在 1984 年的十一月，偕同了康、布雷契與格拉提亞斯，謝西曼等人終於在 Physical Review Letters 這份期刊中，共同發表了他的數據。這篇論文像顆炸彈一般，投在結晶學者之間。它質疑了他們的科學學門中的最基本教條：所有的晶體具有重複的週期性結構模式。

揭開知識的迷障

現在這項發現觸及了更多的讀者，而謝西曼成為了更多批評的目標。不過，在此同時，全世界的結晶學者們都產生了一種似曾相識的感覺，許多人在分析一些其它的物質時，也曾經得到過類似的繞射圖紋，但是當初，他們都將之視為巒晶的證據。現在，他們開始翻箱倒櫃，找出以前的實驗記錄簿，很快發現有些其它的晶體也會產生這種看似不可能的圖紋，譬如八重和十二重的對稱。

在謝西曼發表了他的發現之後，他仍然不知道那個奇怪的晶體內部結構到底如何。顯然地，它的對稱性是五重的，那是何種堆疊方式呢？這個答案卻從另一個未曾料到的領域而得：數學中的馬賽克遊戲。

用以解謎的馬賽克

數學家們喜歡用迷團和邏輯問題來挑戰自我。於 1960 年代，他們開始思索是否可以用有限數目的圖案塊，舖出不會重複的馬賽克圖案，創造一種所謂的「非週期馬賽克」。

頭一個成功的嘗試是在 1966 年，由一位美國的數學家所發表，但是他需要超過兩萬種圖案塊來做到，這很難讓著迷於精簡的數學家滿足。當更多的數學家投入這項挑戰，需要的不同圖案塊數目穩定下修。

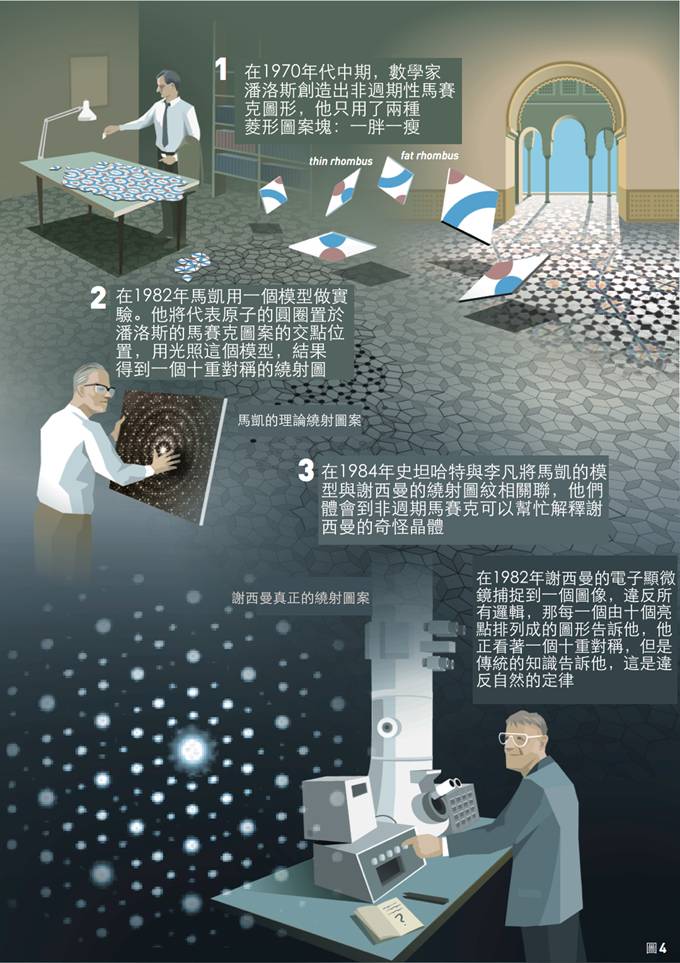
終於，在 1970 年代中期，一位英國數學教授羅傑．潘洛斯（Roger Penrose）對此問題提出了一個最漂亮的解答。他用僅僅兩種圖案塊創造出非週期馬賽克，例如一胖一瘦的菱形（圖 4-1）。

潘洛斯的馬賽克在好幾個不同方面啟發了學界，其中之一是他的發現被用來分析中世紀伊斯蘭綺理（Girih）圖案。我們也發現阿拉伯藝術家早在 13 世紀就創造出了非週期馬賽克，這種馬賽克裝飾著非凡的西班牙阿罕布拉宮，還有伊朗 Darb-i Imam 寺廟的入口和穹頂。

結晶學者艾倫．馬凱（Alan Mackay）運用潘洛斯的馬賽克於另一個方面，他想探究構成物質的原子是否也能如同非週期馬賽克的圖案般排列。他做了一個實驗，用代表原子的圓圈放置在潘洛斯的馬賽克圖案的交點位置（圖 4-2），然後用這樣的圖案作成繞射光柵，來看會得到何種繞射圖案，結果得到一個十重對稱——十個光點圍成一圈。

馬凱的模型與謝西曼的繞射圖紋之間的關聯性，接著被物理學家保羅．史坦哈特（Paul Steinhardt）與多夫．李凡（Dov Levine）所發現。謝西曼的論文在 Physical Review Letters 這份期刊上發表之前，編輯將該文稿交由其他的科學家審核，在這個過程中，史坦哈特有機會看到這份文章，他早就對馬凱的模型熟悉，因此體認到馬凱的理論模型，存在現實世界中，亦存在於謝西曼在 NIST 的實驗室裡。

在 1984 年的聖誕夜，就在謝西曼的論文出刊後的四週，史坦哈特與李凡發表了一篇論文，其中描述了準晶體（quasicrystal）以及它的非週期馬賽克排列。在這篇論文中，準晶體得到了它的名字。

關鍵的黃金比例

準晶體與非週期馬賽克具有一項共同的迷人特質，那是一個在數學與藝術中不斷出現的黃金比例，亦即數學常數 tau。例如：在潘洛斯的馬賽克中，胖的和瘦的菱形數目的比例是 tau；類似地，準晶體中原子間的不同距離的比例，總是與 tau 相關。

13 世紀的義大利數學家費布那西（Fibonacci），從一個有關兔子繁殖的假設性實驗中找到的一系列數字中，描述了這個數學常數 tau。在這個著名的數列中，每一個數字是前兩個數字之和：1、1、2、3、5、8、13、21、34、55、89、144 等等。如果將一個費氏數列中較大的數字除以前一個數字，例如 144/89，你就會得到一個接近黃金比例的數字。

當科學家想要用一個繞射圖紋來描述準晶體中的原子排列時，費氏數列與黃金比例對他們是很重要的。費氏數列也可以解釋 2011 年的諾貝爾化學獎所表彰的發現，為何改變了化學家對晶體結構的規律性之看法。

不會重複的規律

先前，化學家解釋晶體的規律性在於一個週期性不斷重複的模式。費氏數列雖然不會重複，卻也是規律的，因為它遵守一個數學的規則。

在準晶體中，原子間的距離與費氏數列相關，原子以規律的方式排列，化學家可以預測一個準晶體中的結構是何樣，不過這種規律性與具有周期性結構的晶體是不同的。

在 1992 年，這個認知導致了國際結晶學會改變了他們對晶體的定義。先前對晶體的定義是「一個物質，其中組成的原子、分子或離子以一個整齊而且重複的方式堆疊成立體的型態」，現在新的定義是「任何固體，基本上具有可區別的繞射圖紋」，這個定義比較寬廣，而且允許未來可能發現的其它種晶體。

準晶體也存在於…

從他們 1982 年的發現之後，數以百計的準晶體在全球許多實驗室中被合成，但一直到了 2009 年的夏天，科學家才第一次報導了天然的準晶體。他們發現了一種採自東俄的哈吐卡（Khatyrka）河的樣本中之礦石。這種礦石是由鋁、銅和鐵組成，具有一個十重對稱的繞射圖紋。它被稱為二十面石（icosahedrite），此名源自於二十面體（icosahedron），那是一種具有 20 個正三角形面的幾何固體，黃金比例存在於其幾何結構中。

準晶體也被發現存在於一種世界上最耐用的鐵當中。在嘗試不同組合的金屬時，一家瑞典的公司成功的製備出一種鐵，具有許多令人驚訝的良好特質。分析它的原子排列結構時，顯示它具有兩種相：硬鐵的準晶體嵌在一種較軟的鐵中，此一準晶體具有一種盔甲的功能。現在它被用於刮鬍刀片，以及眼睛手術的細針等產品中。

除了特別堅硬外，準晶體能像玻璃般輕易的碎裂。

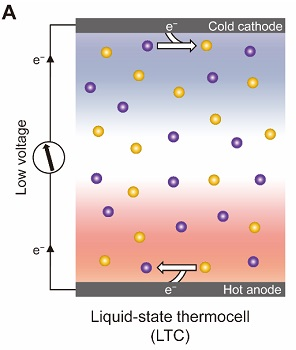
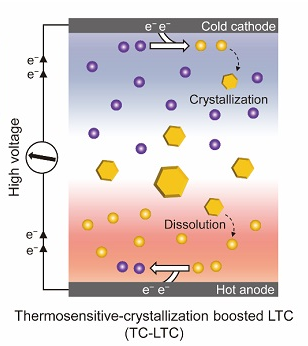
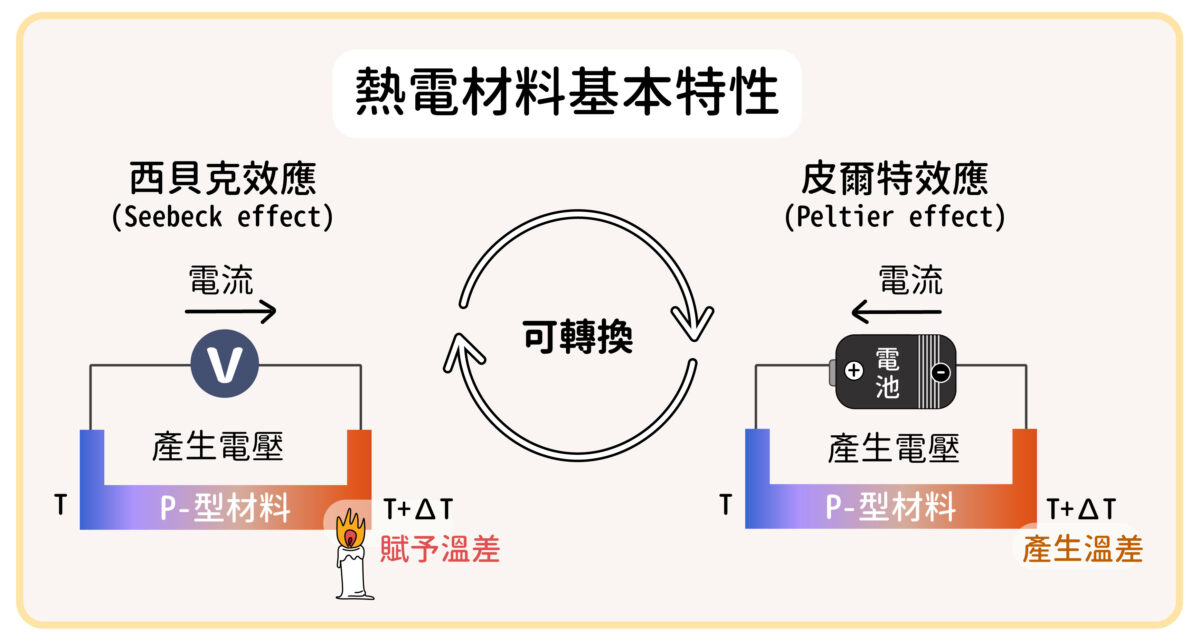
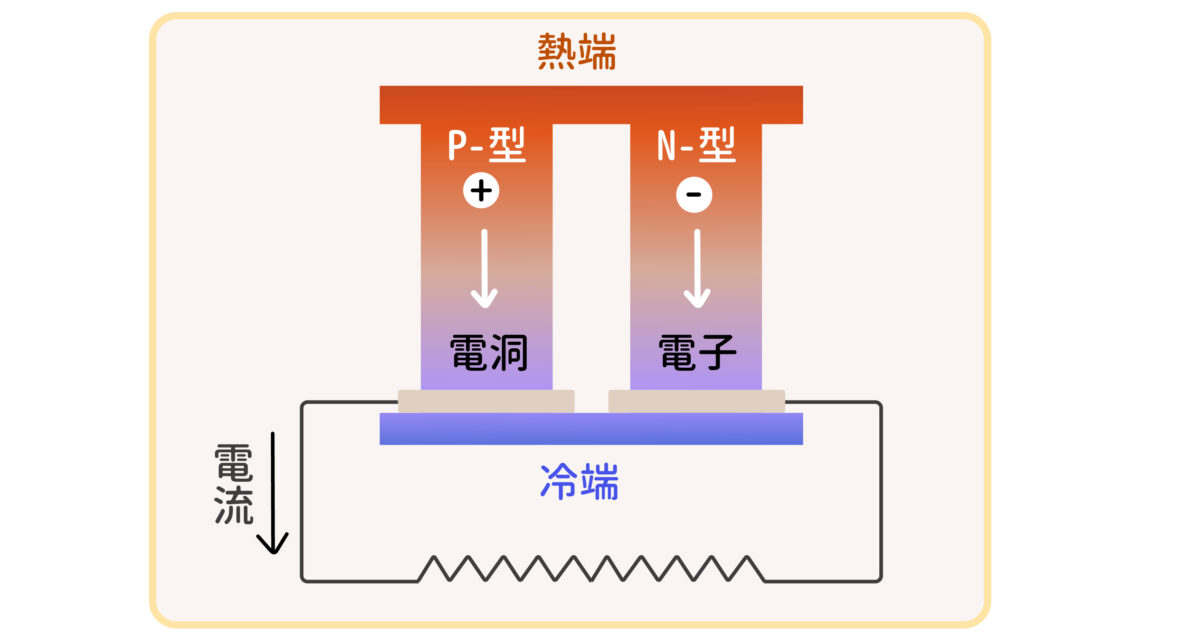
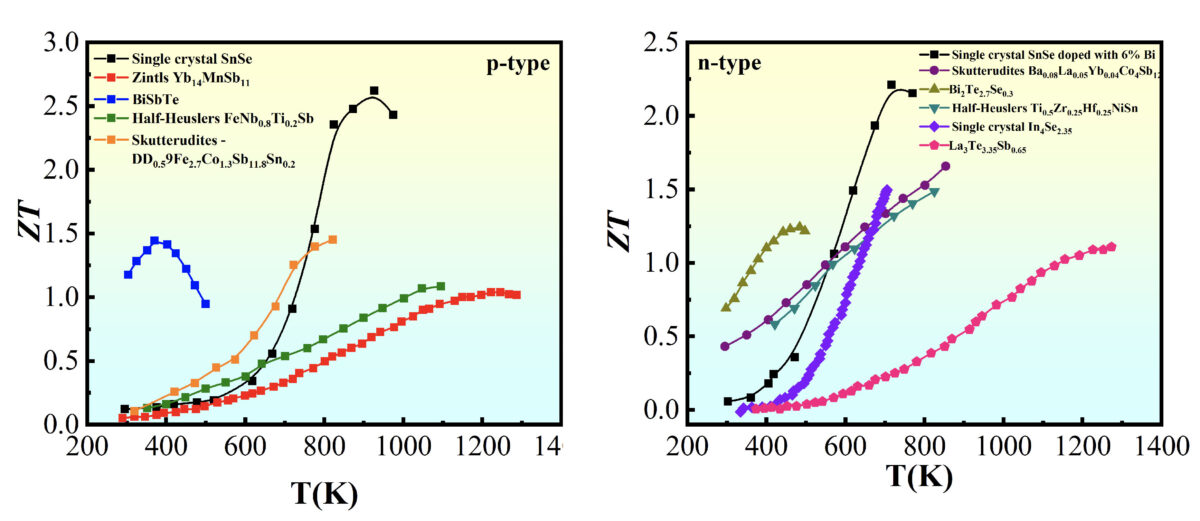
由於其特殊原子排列結構，它們也是很差的熱與電的導體，以及含有不具黏性的表面。其低熱傳導的性質可以讓它們成為有用的熱電材料，能將熱轉為電，發展這種材料的目的在解決熱能的再利用，例如用在汽車與卡車上。現在科學家們正在實驗將準晶體用做像是煎鍋，以及節能的發光二極體（LED）之表面塗料，或是作為引擎的隔熱等等。

保持開放的心

謝西曼的故事並非唯一。

在科學的歷史中，一再地有研究工作者被迫與已經建立的「真理」作戰。事後看來，那些真理不過是一些假設。謝西曼和他的準晶體所面對過的最嚴厲批評，來自於鮑林（Linus Pauling），他曾得過兩次諾貝爾獎。這很清楚地顯示，即使是我們最偉大的科學家，也無法免疫於被陷在舊教條當中。

保持一個開放的心態，勇於質疑已經建立的知識，實際上可能是科學家們最重要的性格特質。

參考資料

• 本文譯自諾貝爾化學獎委員會公佈給大眾的新聞稿：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/info_publ_eng_2011.pdf
• 若需要進一步的資訊，請至以下網頁點選：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/sciback_2011.pdf

本文轉載自中央研究院研之有物，泛科學為宣傳推廣執行單位。

• 採訪撰文｜郭雅欣
• 美術設計｜林洵安

回收廢熱的熱電材料

在全球面臨能源轉型之際，再生能源的發展大多著重在太陽能、風力、水力、生質燃料等。然而近年，隨著奈米科技的發展，可將廢熱轉為電力的熱電材料也逐漸嶄露頭角。中央研究院物理研究所陳洋元研究員踏足熱電材料的研究已有十幾年，在他眼中，熱電材料極具能源發展潛力。

熱電轉換再興起

身處能源轉型的關鍵時刻，我們不由得擔心，再生能源真的足以補上電力缺口嗎？還有沒有其他新興的發電方法呢？有的！用廢熱發電，聽起來很不錯吧？畢竟在日常生活中，我們也受夠廢熱了。汽車、冷氣等機械廢熱，加上太陽的輻射熱等，這些煩人的廢熱如果能拿來發電，實在是個好主意。

熱電材料就是熱生電的關鍵，它能將（沒用的）熱轉化成（好用的）電。近年來，熱電材料逐漸發展起來，中研院物理所研究員陳洋元從 2006 年起開始研究熱電材料，他說：「熱電材料的發電效率已經有很大的進展！」在不久的未來，熱電材料的應用將愈來愈廣泛，成為能源轉型時代的重要一角。

熱電材料的歷史要回溯到 200 年前，德國科學家西貝克（Thomas Seebeck）在 1821 年發現，材料兩端的溫度差會形成電位差，稱為「西貝克效應」。也就是說，同一種材料只要兩端溫度不同，兩端之間就會產生電壓；反之，在材料兩端賦予電壓時，兩端之間就會產生溫度差。科學家因此定義了西貝克係數 S = ^∆V⁄_∆T，表示同一種材料下，溫度差愈大，輸出電壓越大，「換句話說，一個有溫差的材料，等於可以視為一個乾電池。」陳洋元解釋。這便是熱電材料的基本物理機制。

找出最優質的熱電材料

由於每一度溫差產生的電壓就是「西貝克係數」，直觀來說，西貝克係數愈大的材料，在同樣的溫差下輸出的電壓愈大，是愈好的熱電材料。不過陳洋元補充說，熱電材料除了西貝克係數要高之外，「導電性也要好，除此之外，導熱率不能太好，否則溫差一下子就熱平衡掉了。」考量各種條件之後，科學家訂出了熱電材料的優質係數 ZT 值=（^δS2⁄_κ）T，其中 σ 是導電係數、S 是西貝克係數，κ 是導熱率，T 是絕對溫度。

導電性好、西貝克係數高，而且導熱率要低。這是優質熱電材料的三大條件。

於是，研究熱電材料的科學家從幾十年前開始，便朝著符合這些條件的方向努力。陳洋元說：「金屬的導熱都太好了，並不適合當作熱電材料。目前主要的做法是用各種半導體材料，搭配不同的摻雜元素及比例，來找出最佳化的 ZT 值。」

全世界各研究團隊多年下來，針對各種材料組合及摻雜比例，找出了不少值得關注的熱電材料候選者（如下表）。「你可以從中發現，多數的熱電材料都是溫度愈高，ZT 值愈高，在 600°C~700°C 的高溫會表現得很好。」陳洋元笑說：「只有一種材料適合在室溫運作，就是鉍-銻-碲（BiSbTe），目前為止無人能出其右。而且科學家大概 50 年前就發現它了，它保持世界紀錄至今 50 年。」

控制晶格和缺陷，不讓熱傳過去！

找到優秀的材料搭配和比例還不夠！要提升熱電效果，還有一個重要因子：減低熱電材料的導熱率。微觀來看，就是精細地調控材料晶格或內部缺陷。

晶格是材料的骨架，熱的本質是晶格振動，而熱傳導的本質便是晶格裡的原子以振動方式將能量傳遞給鄰近原子。因此，阻礙能量傳遞的方式，就是調控材料內原子的排列，以期達到導熱差、導電好的最終目的。

理想上可以利用「超晶格」，當不同種類的原子像三明治一般層層交替堆疊時，界面的原子與鄰近原子尺寸、重量都不同，這會造成晶格排列不順暢（晶格不匹配），彼此的振動能量也不易傳遞，大部分都會反彈回來，也就達到「導熱不佳」的效果了。

種類不同、尺寸與重量皆不同的原子間，由於晶格不匹配，振動比較不易傳遞，導熱率因此降低。

陳洋元進一步解釋，超晶格的每一層材料厚度、比例都必須嚴格控制，「因為我們只希望導熱率降低，但不希望影響到電子的移動。」也因此，這項製程「非常困難，需要的設備也很昂貴。超晶格結構如果要做到一張紙那麼厚，可能必須鍍膜上萬次，成本很高，東西也做不大。換言之，超晶格在學理上可行，但實際應用上有困難。」

「我們可以選擇退而求其次的做法。」陳洋元說。例如在材料裡刻意摻雜一些雜質，或製造晶格的空缺，包括：點缺陷、空位、差排、疊差等。以這些缺陷的數量來控制材料特性，在盡量不影響導電的狀況下降低熱傳導率。「這是比較簡單可行的做法。」

熱電材料自有用武之地

熱電材料在實際應用上，發展得比其他再生能源慢，主要原因還是在發電效率不夠好。目前在室溫下最好的熱電材料，轉換效率約 3~4%，相較之下，太陽能發電目前的轉換效率約在 15~20%。這也是熱電材料在能源發展上較少被提及的主因。

「不過其實熱電材料在 600°C~700°C 的高溫下，轉換效率可以超過 10%。」陳洋元說。因此，幾年前美國一度打算將熱電材料用在汽車的廢熱回收，畢竟燃油引擎的油電轉換效率大約在 30% 左右。「剩下的 70% 都變成廢熱排出去了。如果能把其中 10% 的廢熱轉換成電能，等於是引擎效率的一大躍進。」不過後來，隨著電動車逐漸成為主流發展方向，這項應用也就失去關注了。

熱電材料就這樣無英雄用武之地了嗎？並不是。其實早在 30~40 年前，它就已經應用在太空科技上了。太空船或衛星發射到太空中之後，需要電能維持運作，除了太陽能以外，熱電也是重要的電力來源。陳洋元以航海家一號舉例，「它朝著太陽系外離去，過程中太陽光會愈來愈微弱，因此不能完全仰賴太陽能做為電力來源。」因此，航海家一號就有使用熱電技術，其中熱的來源是鈾、鈽等放射性材料，它們在衰變過程會放熱，與外太空趨近絕對零度的環境產生溫差，藉此發電。「這些放射性材料的半衰期是幾十億年，對我們來說像是萬年之毒，但對太空船來說，卻像是永恆的電力來源。」陳洋元說。

熱電轉換效率不佳，但對於缺乏電力來源、外界環境溫度極低，又不怕放射性汙染的太空科技來說，是很好的發電選擇。

此外，熱電材料不只能把熱轉換成電，也能反過來，利用材料兩端的電壓差回推來產生溫度差。也就是說熱電材料的應用不限於發電，它也能做為冷氣、冰箱等使用的溫度計；或是在熱電材料上外加電壓，產生電流，造成材料兩端的溫度差，做為冰箱、電腦 CPU 的致冷元件。

陳洋元也在近兩年，研究開發出薄型熱電晶片，裡面的結構是 128 對微小的 p 型、n 型半導體柱，就像 128 個小小的乾電池串聯一樣，能把熱電效應放大百倍。陳洋元解釋，雖然熱電效率不高，無法用在大型工廠等需要巨大電量的狀況，但這樣的晶片可以用來製作「熱電自充隨身電源」，應用在手機或電子手錶等隨身穿戴式電子裝置上，這類裝置需要的電量不高，但可能隨時有充電需求。「想像一下這樣的場景，你走在路上發現手機沒電了，於是拿出熱電自充隨身電源，利用自身體溫與室溫的溫差，幫手機緊急充電。」

隨著網際網路的發展，基地台熱點愈來愈多，這也讓陳洋元對於熱電材料的應用潛力更加樂觀。「在某些偏遠地帶，例如玉山的基地台，電力供給或許就不需要建置發電站，利用熱電材料（透過溫差發電的特性），只要送一桶瓦斯去就好，方便多了！」或者，熱電材料也能與太陽能互補，「因為太陽能發電使用的是太陽光，它的輻射熱並沒有被利用到，這一點可以用熱電材料來加強補足。」陳洋元說。

另外，陳洋元也正在與廠商合作，希望能製作中型、大型的發電機。陳洋元說：「一個熱電晶片大約能發 20 瓦的電，把 25 個晶片合起來，就能有 500 瓦。」儘管成本比一般發電機高，但熱電發電機具有輕巧、無噪音等優點，「我相信它在未來是一個機會。」

熱電材料的研究還在如火如荼的進展著，而陳洋元對它的未來也抱持著樂觀的態度。回頭看看熱電材料的優質係數 ZT 值，「只要我們想辦法降低導熱率，它理論上還能再拉高。」陳洋元說：「現在室溫下的 ZT 值最高是 1 點多，在不久的未來，我們很有可能就突破它了」