民進黨初選民調,其五個執行單位的結果一致且相近,是否值得懷疑?
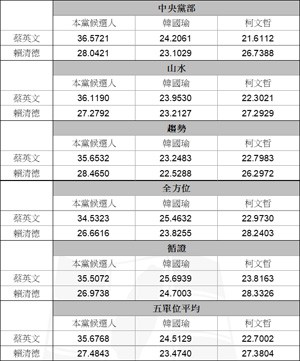
關於這個問題,民進黨的官方答覆是:「此次總統初選民調方式,各執行單位的成功樣本高達 3200 份以上(95%信心水準下,抽樣誤差為正負1.7%),且為本黨民調中心抽樣提供給五家民調單位同時訪問,在相同的抽樣架構、相同的問卷題目、相同的訪問原則、相同的訪員訓練,相同的加權方式之下執行。有相近的民調結果才顯見此次總統初選民調的品質值得信賴,如果五家單位的民調結果差異過大,那才是值得擔憂的事。」
這個答覆令人滿意嗎?
民調得出接近的結果,究竟是否有「異常」?先從假設談起

五個單位關於蔡英文支持度的結果分別為:36.5721%、36.1190%、36.6532%、34.5323%、35.5072%,其平均數為 35.6768%。五單位的結果偏離平均數最大值為 1.1445%,這個值比 95% 信心水準下的抽樣誤差正負 1.7% 要小很多。
按照民進黨的說法,似乎各單位民調結果越相近,民調的品質越值得信賴,真的是這樣嗎?五個單位的結果距離其平均數不超過 1.1445% 的機率是多少?如果這個機率甚小,難道我們不應該擔憂?
要探討這個問題,必須要做一些假設,以下的假設其實不盡成立,但本文的目的並不在於檢定這些假設的真假,而是在於利用統計學「抽樣分佈」(sampling distribution)的概念來看在「正常」狀態下,五個重複樣本結果相近的程度是否有「異常」的跡象。做這些假設只是為了要提供一個「正常狀態」的框架而已。
假設一:各民調單位的樣本是同一母體的的隨機樣本,其樣本數同為 N=3200。
這個假設除了樣本數外,會有很多爭議。
第一、所謂母體是指甚麼?全體合格選民?當然不是。
民進黨所從以抽樣的母體其實有兩個:市話號碼和手機號碼。這是兩個不一樣的母體,而且不論分別開來或合併起來,都不能反映全體合格選民。
第二、各單位的樣本是市話加手機混合母體的隨機樣本嗎?當然不是。
根據民進黨的計算,市話被抽中的機率是 0.19%,手機被抽中的機率是 0.05%。既然市話跟手機被抽中的機率不一樣,各單位的混合樣本就不是混合母體的隨機樣本,更不是全體選民的隨機樣本。
如果民進黨能把市話樣本和手機樣本分別開來,則市話樣本可以說是市話母體的隨機樣本,手機樣本可以說是手機母體的隨機樣本。但因為民進黨只公布每單位市話和手機混合樣本的資料,這裡的假設只是純粹正常狀態的假設。
假設二:支持度的母體參數值(π)可以用各單位樣本支持度(P)的平均數來估計。
本來在同一母體重複抽取足夠多的隨機樣本時,樣本的平均支持度會是母體真正支持度的不偏估計。但如果這些重複樣本不是隨機樣本,則這個假設不必然成立。另外,五個重複樣本並不能算「足夠多」,所以這個假設也只是純粹假設。
假設三、各樣本對人口變數的加權對結果的影響可以忽略。
這個假設通常是可以接受的,但因為民進黨未公布未加權的結果,加權究竟影響有多大也無從得知。
根據這些假設,得到此結果的機率是……?
根據假設一,應用中央極限定理(CLT)可以導出樣本支持度 P 的「抽樣分佈」是常態分佈:
P~N(π,π(1-π)/N)
其期望值π 是母體支持度,變異量是 π(1-π)/N。值得注意的是:變異量是 π(1-π) 的函數,因為 π 增加時 1-π 減少,π 減小時 1-π 增加,這個分佈的「胖」、「瘦」對 π 並不敏感。因為這樣,以下機率的計算與母體支持度大小的關係不大,關係較大的是五樣本支持度相近的程度。
我們先分析蔡英文支持度的相近程度,再用同樣的方法分析賴清德、韓國瑜、柯文哲的支持度。根據上面的假設,蔡英文母體支持度參數值估計為π=0.356768,由此求出的變異量是 0.0000717139,標準差是 0.008468。所以:
P~N(0.356768,0.008468^2)
也就是平均數為 0.356768,標準差為 0.008468 的常態分佈。這個常態分佈就是上面所說的「正常狀態」,當足夠多的機構「在相同的抽樣架構、相同的問卷題目、相同的訪問原則、相同的訪員訓練,相同的加權方式之下執行」執行民調時,其所得到的樣本支持度理論上應該遵行這個常態分佈。我們要算五個單位結果那麼相近的機率必須要在這個常態分佈之下來算。
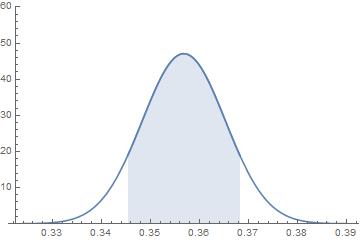
在這樣的常態分佈之下,每一樣本支持度距離 35.6768% 不超過 1.1445%,也就是落在 (34.5323%,36.8213%) 區間內的機率是 0.823463,這就是下圖曲線下藍色區域的面積。
如果要算五個民調的支持度同時落在此區間內,則其機率是 0.823463^5≈0.38。
這個機率是大是小呢?
一般所說的「信心區間」可以有兩個意義。 以支持度比例來說,教科書所說的信心區間是指樣本比例加減由樣本比例算出來的抽樣誤差估計值所得到的區間。但如果我們知道母體比例,則也可以把母體比例加減由母體比例算出來的抽樣誤差來建構信心區間。
這裡因為假設二,我們可以從第二種意義來看待「95%信心區間」:樣本支持度落在以母體支持度為中心的這個區間的機率為 0.95。如果我們有五個重複樣本,則這五個樣本的支持度全部落在「95%信心區間」之內的機率是 0.95^5≈0.77。
上面算出的 0.38 是在正常狀態之下,五個重複樣本支持度距離母體支持度不超過 1.1445% 的機率。

現在民進黨五個執行單位得到的蔡英文支持度均在此區間之內,因此有 0.38 機率發生的事件發生了,這樣奇怪嗎?如果摸彩中獎的機率約 0.40,而你中獎了,你會覺得有人作弊讓你中獎嗎?我想多數人不會覺得這樣中獎有什麼好奇怪的。
這機率可以看做是統計檢定的 p值,也就是數據與假設相諧的程度。0.38 比 0.77小,但它並未小到讓我們得出數據與假設不相諧的結論。
當然,就如統計檢定 p>0.05 並不代表虛無假設為真一樣,它也不足以讓我們做出假設一至三為真的結論。(請參考拙作〈看電影學統計:p值的陷阱〉)

用同樣的方法分析各單位測得的賴清德、韓國瑜、柯文哲對比支持度,都可以得到類似的結果。五個重複樣本的支持度落在實際發生區間內的機率為:0.30(賴清德)、0.60(韓國瑜對比蔡柯)、0.58(韓國瑜對比賴柯)、0.49(柯文哲對比蔡韓)、0.40(柯文哲對比賴韓)。這些機率均未小到令人起疑的地步。
統計上,差異過大或差異過小都可能有問題
民進黨說「有相近的民調結果才顯見此次總統初選民調的品質值得信賴,如果五家單位的民調結果差異過大,那才是值得擔憂的事。」其實是不對的。差異過大固然值得擔憂,太過相近也是問題。
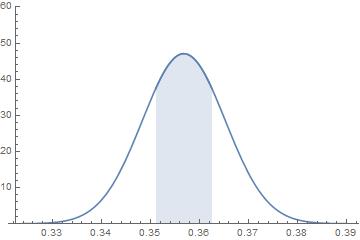
比如我們把五單位的蔡英文支持度偏離其平均數的最大值減半至 0.5723%,則母體支持度加減 0.5723%的區間便縮小為下圖藍色區域。單一樣本的支持度落在此區間內的機率大約是 0.5,五個樣本支持度全部落在此區間內的機率只有 0.5^5≈0.03。這樣小的機率只能讓我們得到數據與假設不相諧的結論。
民進黨應該解釋的是五單位民調的結果並沒有相近到不可思議的地步,而不是說相異過大才值得擔憂。民調太相近或太相異都是品質可能有問題的跡象。
後記
本文完成後,看到ptt上有高手(raiderho)更早就用模擬的方法得到五單位民調相近程度並非小機率事件的結論。該文雖然用的是模擬的方法,卻能以對比民調中四個比例(蔡/賴、韓、柯、未表態)的聯合常態分佈為基礎來計算機率,可以補本文只用邊際分佈計算機率之不足。
請參考:
本文轉載自作者部落格,原文標題:民進黨初選民調的「抽樣分佈」