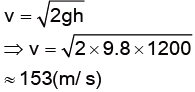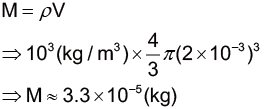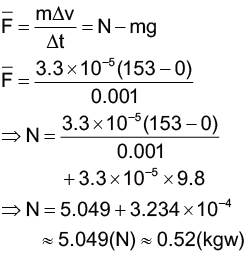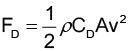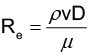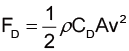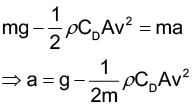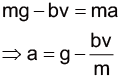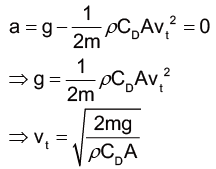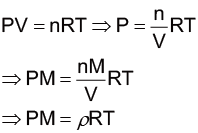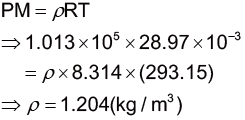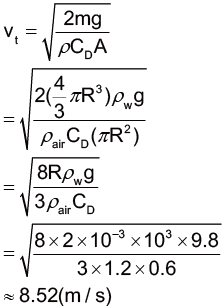「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中組專題報導類第三名之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:王治鈞、呂建霆、洪林竹/國立科學工業區實驗高級中學。

序章
在世界級奇幻名著《魔戒》改編的電影《魔戒首部曲:魔戒現身》之中,反派角色「炎魔」和全書靈魂角色「甘道夫 」在摩瑞亞礦山中的武打場面非常精彩,並因此常常為魔戒粉絲們津津樂道。
讓我們先把目光放回中土大陸的摩瑞亞礦山。在一場驚心動魄的激戰之中,住在礦山中的怪獸——炎魔因腳下的橋樑突然崩落而墜入底下的深淵。就在甘道夫鬆了一口氣的時候,陰魂不散的炎魔在墜落過程中甩出火鞭纏繞住甘道夫的膝蓋,使得甘道夫跌了一跤,並跟炎魔一樣摔了下去。
在電影中,從炎魔開始墜落的那一刻起到甘道夫墜落,整個過程共約 32 秒。但是,最後甘道夫和炎魔卻「同時」墜入一個地底湖中,並且繼續激戰。
相信不少人在看到這一幕的時候都會被電影逼真的特效和磅礡的畫面所震懾,我們也不例外。而在此同時,我們更聯想到一個問題:……是不是有哪裡怪怪的?
讓我們先再次整理條件:
- 伽利略告訴我們,在同個高度下,不同物體掉到地上的時間皆應相同
- 炎魔比甘道夫更早開始下墜
- 更精確地說,炎魔早了32秒
從上述條件我們似乎可以得到一個結論——炎魔應該要比甘道夫早 32 秒掉到地底湖中才對。電影情節終究只是虛構,是不可能發生的。
但是,這真的完全不可能嗎?
難道《魔戒》不是真的?
難道約翰·托爾金(《魔戒》原著作者)騙了我?
難道我這輩子最愛的小說其實盡是謊話連篇的荒唐之論?
先暫且不論「《魔戒》本來就是歸類在『奇幻作品』中,所以一切皆有可能」,在數理上,電影中的情節究竟有沒有可能呢?
剛才的推導是建立在十分簡單的假設上,所以結果可能和真實的情況不太一樣。接下來,我們將利用一些詳細的資訊分析當他們墜落深淵時到底會發生什麼事,更定量地討論「同時到達底部」這個結果的合理性。
加入「空氣阻力」的條件
在這個段落裡面,我們將會逐一進行下列步驟:
- 寫出甘道夫和炎魔墜落時所必須遵守的運動方程式
- 根據電影本身和其他資料估計一些參數(像是質量、空氣密度等)
- 解微分方程
- 把之前估計的參數代回式子中解完方程
- 回答我們提出來的問題——甘道夫和炎魔到底會不會同時墜地?
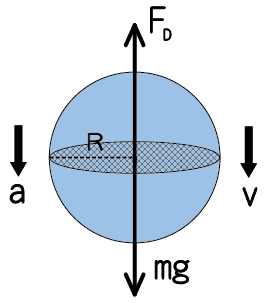
首先,翻閱課本便可以知道空氣阻力的公式和運動方程式是
$$ F = \frac{1}{2}ρC_DAv^2 $$
\( ma\)\(=m\frac{dv}{dt}\)\(=F-mg \)\(=\frac{1}{2}ρC_DAv^2-mg \)
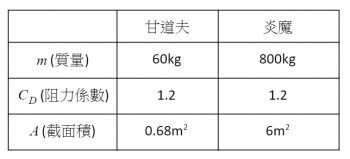
其中m是質量、ρ空氣密度、CD阻力係數、A截面積、v速度。空氣密度大約是 1.29kg/m3,其他的參數我們必須根據電影和其他網路上的資料來估計。
下面這個表格分別列出甘道夫和炎魔的參數:
讓我們解釋一下這些估計是怎麼來的。
首先,根據Tolkien Gateway (類似魔戒專屬的維基百科)的資料,甘道夫的身高約 1.67 公尺,體重則並未提及。如果甘道夫是一個健康的巫師,我們可以預期他的 BMI 是 21,並進一步推得體重大約是 60 kg。
炎魔的話比較麻煩些,維基百科上寫炎魔站起來約人類的 3 倍高。假設炎魔的肌肉能承受的壓力和人類的一樣強,那麼肌肉截面積可估計為32=9倍,能承受的重量也是人類平均重量的32=9倍。不過我們可以合理地推測炎魔應該比人類強壯一些,所以實際上的重量應該大於60×9=540(kg),在這邊估計800kg。
至於阻力係數,則是和身體的形狀有關。根據這篇論文,人的阻力係數大約是1.2,因為炎魔大致上也是人形,在這邊就假設阻力係數一樣。另外,根據這篇皇家氣象學會的論文,人體的截面積約0.68m2,而從電影畫面估計,炎魔的截面積大約是6m2。
現在回到方程式的部分, 為了讓方程式好看一點,我們可以定義
$$ γ\equiv \frac{1}{2m}ρC_DA $$
,所以對於甘道夫和炎魔來說,他們的 γ 分別是 0.0088 和 0.0058。
\(\frac{dv}{dt}\)\(=γv^2-g, \int \frac{dv}{γv^2-g}\)\(=\int dt\)
\(\frac{1}{2\sqrt{γg}}(ln(\sqrt{\frac{g}{γ}}-v)-ln(v+\sqrt{\frac{g}{γ}}))\)\(=t+t_0\)
\(v=-\sqrt{\frac{g}{γ}} \tan{h}\tan{h}[\sqrt{gγ}(t+t_0)]\)
\(y=\int_{0}^{t}vd{t}’\)\(=-γ^{-1}\ln \ln\cos{h}\cos{h}\sqrt{gγt}\)
t0是積分常數,如果把t=0設定成開始墜落的時間,那麼 t0 應該是0,這樣一開始的速率才會是0 (因為 tanh0=0)。底下兩個式子中的第一個告訴我們當一個法師(或是某種遠古怪獸)墜入深淵時,速度和時間的關係;而第二個則是掉落距離和時間的關係。我們需要知道的只有 γ,而這和掉落物本身的性質有關。
我們可以發現當時間 t 越來越大的時候,tanh 後面的參數也會越來越大,這會讓 tanh 的值接近1,這時候速率接近\(\sqrt{\frac{g}{γ}}\),就是終端速率。而 y 則是墜落深度和時間的關係。
炎魔比甘道夫早32秒出發,這代表牠在這32秒內已經先掉落了\( 0.0058^{-1}\ln\ln\cos{h}\cos{h}(\sqrt{9.8\cdot 0.0058\cdot 32})\)\(\approx 1200(m)\)
,甘道夫才開始往下掉。
由於tanh x 在 x 比 2 大的時候會十分接近 1。如果要讓√gγt 等於 2,對於甘道夫和炎魔來說,都需要經過約 7 到 8 秒。經過 32 秒後,炎魔的速率已經幾乎等於終端速率了,也就是\(\sqrt{\frac{g}{γ_B}}\approx 41(m/s)\);而這時候甘道夫才剛墜落,不過無論如何,他最多也只能和終端速率\(\sqrt{\frac{g}{γ_G}}\approx 33(m/s)\) 一樣快,在這樣的情況下,甘道夫是永遠沒辦法追上炎魔的。(上面的 \(γ_B\) 和 \(γ_G\) 分別代表炎魔和甘道夫的 \(γ\),如前所述,它們分別是 0.0058 和0.0088。)
因此,在將空氣阻力納入考量的情況下,我們發現甘道夫還是沒辦法在掉落過程中趕上炎魔。
關於炎魔的鞭子
經過上述探討,我們還可以算算看炎魔的鞭子大約有多長。電影中炎魔的鞭子在牠墜落大約14秒後從深淵伸上來打到甘道夫。我們可以利用之前推導過的深度和墜落時間的關係:
\(y=\int_{0}^{t}vd{t}’=-γ^{-1}\ln \ln\cos{h}\cos{h}\sqrt{gγt}\)
來計算。
將t=14和γ=0.0058代入算式,我們可以算出來這時候炎魔已經掉落了約 460 公尺,也就是說,炎魔的鞭子至少要
\( 0.0058^{-1}\ln\ln\cos{h}\cos{h}(\sqrt{g\cdot 0.0058\cdot 14})\)\(\approx 460(m)\)
,才有機會在墜落後 14 秒將鞭子伸上來勾住甘道夫。
結論
在上面的文章中,我們用數學與理性的角度分析了電影《魔戒》中經典的一幕——甘道夫大戰炎魔之後,兩者雙雙墜入深淵。
首先,我們對電影中的情況進行辨析,並發現甘道夫與炎魔同時到達底部似乎不符合科學。接著我們將空氣阻力納入考量並進行運算,但是仍得到相同的結果。換而言之,比較早掉下去的炎魔必定會比甘道夫更早掉到底部。而這結論和電影的畫面並不相符。
但是,這就代表電影都在亂演一通?其實倒也未必。或許是因為我們納入考量的條件不足,抑或是因為參數假設有誤,導致我們的推理出了差錯。
不過這些並不是大問題,因為透過上面這些分析,相信各位看官已經和我們一起體會到了數學的美妙和實用。它不只是一門死板的學科,更是可以應用在生活中、實際地解決問題的有力工具;透過將問題轉化成數學,再把數學答案轉化回問題的解答,很多令人摸不著頭腦的問題都能迎刃而解。
最後,《魔戒》本來就屬於奇幻小說,在看完我們的分析之後,千萬別因為糾結於內容合理性而失去了閱讀這部史詩級巨作的趣味呀!
參考資料
- Tolkien Gateway
- Koo, M. H., & Al-Obaidi, A. S. M. (2013). Calculation of aerodynamic drag of human being in various positions. Department of Mechanical Engineering, Taylor’s University, Malaysia.
- McIlveen, J. F. R. (2002). The everyday effects of wind drag on people. Weather, 57(11), 410-413.