停擺 60 年的《哈德維格-納爾遜問題》在一位生物學家的手上有了新突破！

本文與財團法人臺灣生活美學基金會合作。 

AI 有可能造成人們失業嗎？還是 AI 會成為個人專屬的超級助理？

隨著人工智慧技術的快速發展，AI 與人類之間的關係，成為社會大眾目前最熱烈討論的話題之一，究竟，AI 會成為人類的取代者或是協作者？決定關鍵就在於人們對 AI 的了解和運用能力，唯有人們清楚了解如何使用 AI，才能化 AI 為助力，提高自身的工作效率與生活品質。

有鑑於此，目前正於臺灣當代文化實驗場 C-LAB 展出的「2024 未來媒體藝術節」，特別將展覽主題定調為奇異點（Singularity），透過多重視角探討人工智慧與人類的共生關係。

C-LAB 策展人吳達坤進一步說明，本次展覽規劃了 4 大章節，共集結來自 9 個國家 23 組藝術家團隊的 26 件作品，帶領觀眾從了解 AI 發展歷史開始，到欣賞各種結合科技的藝術創作，再到與藝術一同探索 AI 未來發展，希望觀眾能從中感受科技如何重塑藝術的創造範式，進而更清楚未來該如何與科技共生與共創。

從歷史看未來：AI 技術發展的 3 個高峰

其中，展覽第一章「流動的錨點」邀請了自牧文化 2 名研究者李佳霖和蔡侑霖，從軟體與演算法發展、硬體發展與世界史、文化與藝術三條軸線，平行梳理 AI 技術發展過程。

藉由李佳霖和蔡侑霖長達近半年的調查研究，觀眾對 AI 發展有了清楚的輪廓。自 1956 年達特茅斯會議提出「人工智慧（Artificial Intelligence））」一詞，並明確定出 AI 的任務，例如：自然語言處理、神經網路、計算學理論、隨機性與創造性等，就開啟了全球 AI 研究浪潮，至今將近 70 年的過程間，共迎來三波發展高峰。

第一波技術爆發期確立了自然語言與機器語言的轉換機制，科學家將任務文字化、建立推理規則，再換成機器語言讓機器執行，然而受到演算法及硬體資源限制，使得 AI 只能解決小問題，也因此進入了第一次發展寒冬。

之後隨著專家系統的興起，讓 AI 突破技術瓶頸，進入第二次發展高峰期。專家系統是由邏輯推理系統、資料庫、操作介面三者共載而成，由於部份應用領域的邏輯推理方式是相似的，因此只要搭載不同資料庫，就能解決各種問題，克服過去規則設定無窮盡的挑戰。此外，機器學習、類神經網路等技術也在同一時期誕生，雖然是 AI 技術上的一大創新突破，但最終同樣受到硬體限制、技術成熟度等因素影響，導致 AI 再次進入發展寒冬。

走出第二次寒冬的關鍵在於，IBM 超級電腦深藍（Deep Blue）戰勝了西洋棋世界冠軍 Garry Kasparov，加上美國學者 Geoffrey Hinton 推出了新的類神經網路算法，並使用 GPU 進行模型訓練，不只奠定了 NVIDIA 在 AI 中的地位， 自此之後的 AI 研究也大多聚焦在類神經網路上，不斷的追求創新和突破。

從現在看未來：AI 不僅是工具，也是創作者

隨著時間軸繼續向前推進，如今的 AI 技術不僅深植於類神經網路應用中，更在藝術、創意和日常生活中發揮重要作用，而「2024 未來媒體藝術節」第二章「創造力的轉變」及第三章「創作者的洞見」，便邀請各國藝術家展出運用 AI 與科技的作品。

例如，超現代映畫展出的作品《無限共作 3.0》，乃是由來自創意科技、建築師、動畫與互動媒體等不同領域的藝術家，運用 AI 和新科技共同創作的作品。「人們來到此展區，就像走進一間新科技的實驗室，」吳達坤形容，觀眾在此不僅是被動的觀察者，更是主動的參與者，可以親身感受創作方式的轉移，以及 AI 如何幫助藝術家創作。

而第四章「未完的篇章」則邀請觀眾一起思考未來與 AI 共生的方式。臺灣新媒體創作團隊貳進 2ENTER 展出的作品《虛擬尋根-臺灣》，將 AI 人物化，採用與 AI 對話記錄的方法，探討網路發展的歷史和哲學，並專注於臺灣和全球兩個場景。又如國際非營利創作組織戰略技術展出的作品《無時無刻，無所不在》，則是一套協助青少年數位排毒、數位識毒的方法論，使其更清楚在面對網路資訊時，該如何識別何者為真何者為假，更自信地穿梭在數位世界裡。

透過歷史解析引起共鳴

在「2024 未來媒體藝術節」規劃的 4 大章節裡，第一章回顧 AI 發展史的內容設計，可說是臺灣近年來科技或 AI 相關展覽的一大創舉。

過去，這些展覽多半以藝術家的創作為展出重點，很少看到結合 AI 發展歷程、大眾文明演變及流行文化三大領域的展出內容，但李佳霖和蔡侑霖從大量資料中篩選出重點內容並儘可能完整呈現，讓「2024 未來媒體藝術節」觀眾可以清楚 AI 技術於不同階段的演進變化，及各發展階段背後的全球政治經濟與文化狀態，才能在接下來欣賞展區其他藝術創作時有更多共鳴。

「畢竟展區空間有限，而科技發展史的資訊量又很龐大，在評估哪些事件適合放入展區時，我們常常在心中上演拉鋸戰，」李佳霖笑著分享進行史料研究時的心路歷程。除了從技術的重要性及代表性去評估應該呈現哪些事件，還要兼顧詞條不能太長、資料量不能太多、確保內容正確性及讓觀眾有感等原則，「不過，歷史事件與展覽主題的關聯性，還是最主要的決定因素，」蔡侑霖補充指出。

舉例來說，Google 旗下人工智慧實驗室（DeepMind）開發出的 AI 軟體「AlphaFold」，可以準確預測蛋白質的 3D 立體結構，解決科學家長達 50 年都無法突破的難題，雖然是製藥或疾病學領域相當大的技術突破，但因為與本次展覽主題的關聯性較低，故最終沒有列入此次展出內容中。

除了內容篩選外，在呈現方式上，2位研究者也儘量使用淺顯易懂的方式來呈現某些較為深奧難懂的技術內容，蔡侑霖舉例說明，像某些比較艱深的 AI 概念，便改以視覺化的方式來呈現，為此上網搜尋很多與 AI 相關的影片或圖解內容，從中找尋靈感，最後製作成簡單易懂的動畫，希望幫助觀眾輕鬆快速的理解新科技。

吳達坤最後指出，「2024 未來媒體藝術節」除了展出藝術創作，也跟上國際展會發展趨勢，於展覽期間規劃共 10 幾場不同形式的活動，包括藝術家座談、講座、工作坊及專家導覽，例如：由策展人與專家進行現場導覽、邀請臺灣 AI 實驗室創辦人杜奕瑾以「人工智慧與未來藝術」為題舉辦講座，希望透過帶狀活動創造更多話題，也讓展覽效益不斷發酵，讓更多觀眾都能前來體驗由 AI 驅動的未來創新世界，展望 AI 在藝術與生活中的無限潛力。

展覽資訊：「未來媒體藝術節——奇異點」2024 Future Media FEST-Singularity 
展期 ▎2024.10.04 ( Fri. ) – 12.15 ( Sun. ) 週二至週日12:00-19:00，週一休館
地點 ▎臺灣當代文化實驗場圖書館展演空間、北草坪、聯合餐廳展演空間、通信分隊展演空間
指導單位 ▎文化部
主辦單位 ▎臺灣當代文化實驗場

本文由 建研所 委託，泛科學企劃執行。 

當你走進一棟建築，是否能感受到它對環境的友善？或許不是每個人都意識到，但現今建築不只提供我們居住和工作的空間，更是肩負著重要的永續節能責任。

綠建築標準的誕生，正是為了應對全球氣候變遷與資源匱乏問題，確保建築設計能夠減少資源浪費、降低污染，同時提升我們的生活品質。然而，要成為綠建築並非易事，每一棟建築都需要通過層層關卡，才能獲得標章認證。

為推動環保永續的建築環境，政府自 1999 年起便陸續著手推動「綠建築標章」、「智慧建築標章」以及「綠建材標章」的相關政策。這些標章的設立，旨在透過標準化的建築評估系統，鼓勵建築設計融入生態友善、能源高效及健康安全的原則。並且政府在政策推動時，為鼓勵業界在規劃設計階段即導入綠建築手法，自 2003 年特別辦理優良綠建築作品評選活動。截至 2024 年為止，已有 130 件優良綠建築、31 件優良智慧建築得獎作品，涵蓋學校、醫療機構、公共住宅等各類型建築，不僅提升建築物的整體性能，也彰顯了政府對綠色、智慧建築的重視。

說這麼多，你可能還不明白建築要變「綠」、變「聰明」的過程，要經歷哪些標準與挑戰？

綠建築標章	智慧建築標章	綠建材標章

第一招：依循 EEWH 標準，打造綠建築典範

環境友善和高效率運用資源，是綠建築（green building）的核心理念，但這樣的概念不僅限於外觀或用材這麼簡單，而是涵蓋建築物的整個生命週期，也就是包括規劃、設計、施工、營運和維護階段在內，都要貼合綠建築的價值。

關於綠建築的標準，讓我們先回到 1990 年，當時英國建築研究機構（BRE）首次發布有關「建築研究發展環境評估工具（Building Research Establishment Environmental Assessment Method，BREEAM®）」，是世界上第一個建築永續評估方法。美國則在綠建築委員會成立後，於 1998 年推出「能源與環境設計領導認證」（Leadership in Energy and Environmental Design, LEED）這套評估系統，加速推動了全球綠建築行動。

臺灣在綠建築的制訂上不落人後。由於臺灣地處亞熱帶，氣溫高，濕度也高，得要有一套我們自己的評分規則——臺灣綠建築評估系統「EEWH」應運而生，四個英文字母分別為 Ecology（生態）、Energy saving（節能）、Waste reduction（減廢）以及 Health（健康），分成「合格、銅、銀、黃金和鑽石」共五個等級，設有九大評估指標。

我們就以「台江國家公園」為例，看它如何躍過一道道指標，成為「鑽石級」綠建築的國家公園！

位於臺南市四草大橋旁的「台江國家公園」是臺灣第8座國家公園，也是臺灣唯一的濕地型的國家公園。同時，還是南部行政機關第一座鑽石級的綠建築，其外觀採白色系列，從高空俯瞰，就像在一座小島上座落了許多白色建築群的聚落；從地面看則有臺南鹽山的意象。

因其地形與地理位置的特殊，生物多樣性的保護則成了台江國家公園的首要考量。園區利用既有的魚塭結構，設計自然護岸，保留基地既有的雜木林和灌木草原，並種植原生與誘鳥誘蟲等多樣性植物，採用複層雜生混種綠化。以石籠作為擋土護坡與卵石回填增加了多孔隙，不僅強化了環境的保護力，也提供多樣的生物棲息環境，使這裡成為動植物共生的美好棲地。

第二招：想成綠建築，必用綠建材

要成為一幢優秀好棒棒的綠建築，使用在原料取得、產品製造、應用過程和使用後的再生利用循環中，對地球環境負荷最小、對人類身體健康無害的「綠建材」非常重要。

這種建材最早是在 1988 年國際材料科學研究會上被提出，一路到今日，國際間對此一概念的共識主要包括再使用（reuse）、再循環（recycle）、廢棄物減量（reduce）和低污染（low emission materials）等特性，從而減少化學合成材料產生的生態負荷和能源消耗。同時，使用自然材料與低 VOC（Volatile Organic Compounds，揮發性有機化合物）建材，亦可避免對人體產生危害。

在綠建築標章後，內政部建築研究所也於 2004 年 7 月正式推行綠建材標章制度，以建材生命週期為主軸，提出「健康、生態、高性能、再生」四大方向。舉例來說，為確保室內環境品質，建材必須符合低逸散、低污染、低臭氣等條件；為了防溫室效應的影響，須使用本土材料以節省資源和能源；使用高性能與再生建材，不僅要經久耐用、具高度隔熱和防音等特性，也強調材料本身的再利用性。

在台江國家公園內，綠建材的應用是其獲得 EEWH 認證的重要部分。其不僅在設計結構上體現了生態理念，更在材料選擇上延續了對環境的關懷。園區步道以當地的蚵殼磚鋪設，並利用蚵殼作為建築格柵的填充材料，為鳥類和小生物營造棲息空間，讓「蚵殼磚」不再只是建材，而是與自然共生的橋樑。園區的內部裝修選用礦纖維天花板、矽酸鈣板、企口鋁板等符合綠建材標準的系統天花。牆面則粉刷乳膠漆，整體綠建材使用率為 52.8%。

在日常節能方面，台江國家公園也做了相當細緻的設計。例如，引入樓板下的水面蒸散低溫外氣，屋頂下設置通風空氣層，高處設置排風窗讓熱空氣迅速排出，廊道還配備自動控制的微噴霧系統來降溫。屋頂採用蚵殼與漂流木創造生態棲地，創造空氣層及通風窗引入水面低溫外企，如此一來就能改善事內外氣溫及熱空氣的通風對流，不僅提升了隔熱效果，減少空調需求，讓建築如同「與海共舞」，在減廢與健康方面皆表現優異，展示出綠建築在地化的無限可能。

在綠建材的部分，另外補充獲選為 2023 年優良綠建築的臺南市立九份子國民中小學新建工程，其採用生產過程中二氧化碳排放量較低的建材，比方提高高爐水泥（具高強度、耐久、緻密等特性，重點是發熱量低）的量，並使用能提高混凝土晚期抗壓性、降低混凝土成本與建物碳足跡的「爐石粉」，還用再生透水磚做人行道鋪面。

同樣入選 2023 年綠建築的還有雲林豐泰文教基金會的綠園區，首先，他們捨棄金屬建材，讓高爐水泥使用率達 100%。別具心意的是，他們也將施工開挖的土方做回填，將有高地差的荒地恢復成平坦綠地，本來還有點「工業風」的房舍告別荒蕪，無痛轉綠。

等等，這樣看來建築夠不夠綠的命運，似乎在建材選擇跟設計環節就決定了，是這樣嗎？當然不是，建築是活的，需要持續管理–有智慧的管理。

第三招：智慧管理與科技應用

我們對生態的友善性與資源運用的效率，除了從建築設計與建材的使用等角度介入，也須適度融入「智慧建築」（intelligent buildings）的概念，即運用資通訊科技來提升建築物效能、舒適度與安全性，使空間更人性化。像是透過建築物佈建感測器，用於蒐集環境資料和使用行為，並作為空調、照明等設備、設施運轉操作之重要參考。

為了推動建築與資通訊產業的整合，內政部建築研究所於 2004 年建立了「智慧建築標章」制度，為消費者提供判斷建築物是否善用資通訊感知技術的標準。評估指標經多次修訂，目前是以「基礎設施、維運管理、安全防災、節能管理、健康舒適、智慧創新」等六大項指標作為評估基準。
以節能管理指標為例，為了掌握建築物生命週期中的能耗，需透過系統設備和技術的主動控制來達成低耗與節能的目標，評估重點包含設備效率、節能技術和能源管理三大面向。在健康舒適方面，則在空間整體環境、光環境、溫熱環境、空氣品質、水資源等物理環境，以及健康管理系統和便利服務上進行評估。

樹林藝文綜合大樓在設計與施工過程中，充分展現智慧建築應用綜合佈線、資訊通信、系統整合、設施管理、安全防災、節能管理、健康舒適及智慧創新 8 大指標先進技術，來達成兼顧環保和永續發展的理念，也是利用建築資訊模型（BIM）技術打造的指標性建築，受到國際矚目。

在興建階段，為了保留基地內 4 棵原有老樹，團隊透過測量儀器對老樹外觀進行精細掃描，並將大小等比例匯入 BIM 模型中，讓建築師能清晰掌握樹木與建築物之間的距離，確保施工過程不影響樹木健康。此外，在大樓啟用後，BIM 技術被運用於「電子維護管理系統」，透過 3D 建築資訊模型，提供大樓內設備位置及履歷資料的即時讀取。系統可進行設備的監測和維護，包括保養計畫、異常修繕及耗材管理，讓整棟大樓的全生命週期狀況都能得到妥善管理。

智慧建築導入 BIM 技術的應用，從建造設計擴展至施工和日常管理，使建築生命周期的管理更加智慧化。以 FM 系統 ( Facility Management，簡稱 FM ) 為例，該系統可在雲端進行遠端控制，根據會議室的使用時段靈活調節空調風門，會議期間開啟通往會議室的風門以加強換氣，而非使用時段則可根據二氧化碳濃度調整外氣空調箱的運轉頻率，保持低頻運作，實現節能效果。透過智慧管理提升了節能效益、建築物的維護效率和公共安全管理。

總結

綠建築、綠建材與智慧建築這三大標章共同構建了邁向淨零碳排、居住健康和環境永續的基礎。綠建築標章強調設計與施工的生態友善與節能表現，從源頭減少碳足跡；綠建材標章則確保建材從生產到廢棄的全生命週期中對環境影響最小，並保障居民的健康；智慧建築標章運用科技應用，實現能源的高效管理和室內環境的精準調控，增強了居住的舒適性與安全性。這些標章的綜合應用，讓建築不僅是滿足基本居住需求，更成為實現淨零、促進健康和支持永續的具體實踐。

「晚安，在幹嘛呢？」
「下週要考試了，都唸不完。」
我（世杰）抬頭看螢幕，遊戲「正在讀取中」的長條圖走到 3/4，心裡閃過一絲罪惡感。
「我也正要準備唸書。」我沒說謊，準備再打五場，三小時後唸書。

開始和小昭用 LINE 聊天後，我發現她很認真，每天都在唸書。如果是別人，我早就虧她「今天有去安親班嗎？」、「不，我不是說打工，是說你去上安親班，繳學費的那方。」但小昭只會讓我自慚形穢，她好上進，我好糜爛，連反省也是在遊戲讀取的空檔。

遊戲開始，MathKing 跟我走同一條路線，那是孝和的帳號。
「她每天都用唸書當藉口來拒絕你嗎？」
「我還沒約！」
我點擊滑鼠，對一隻小兵用了絕招，小兵被炸得四分五裂。
「心虛就算了，不要浪費魔法點數。」
「該怎麼幫助小昭唸書更有效率啊？」

我們在系上的電腦教室。雖然可以在家玩，但坐在旁邊並肩作戰的感覺還是比較好，照我剛剛跟小昭的說法是─—留在系上唸書。

「她沒有接著說『改天可以一起唸』……」

孝和盯著螢幕的臉上露出「怎麼可能」的表情。

「用網路聊天很開心，但人與人深交還是需要見面啊，就像我們要坐在一起打電動。」我嘆了口氣說。
「我們只是說垃圾話比較方便。你們也說垃圾話？」
「我們說情話！見面才能看見表情，知道她說話的時候是微笑、大笑，還是嬌羞。見面才能聽見聲音，知道她的語氣是輕快的，還是不帶情感，又或是害羞。」
「你有病，一直希望對方嬌羞害羞。」我用連續技解決掉敵人，繼續說。「見面才能看見整個人，她的手托腮嗎，還是放在桌上？腿上？ 我的手上？」

「這是發花癡，不是在講見面的意義了吧。見面的確有意義， 有更多資訊，就能更了解對方的心思。」

孝和從旁邊突襲，發動範圍技，我們少打多，解決掉三個對手。

「被你說得好像在測謊。」

大概是從我遊戲人物的步伐中看出了沮喪，孝和自以為不著痕跡地安慰我。
「或許她唸書得專心一個人吧。」
「你也這麼覺得嗎！？」
「我們是不是這麼覺得不重要，而是只能這麼覺得。畢竟就算這真的是藉口，你也不能怎樣。哎專心一點！」我的弓箭手角色在會戰時走到最前線，連一發箭都沒射出就領便當了。

孝和對盯著螢幕發呆的我嘆了口氣，說：「不要只會打順手球啊，你應該用數學來一場大逆轉。」

數學唸書術

「唸書其實就是時間管理。大學以前的課業有範圍。作為第一順位，唸書的目標是：用最少時間，學懂該學的知識。得趕快唸完才能去玩。這是一個最佳化問題，目標是時間，限制是要唸的書。」

孝和跟我拉了兩張椅子坐在印表機旁，他繼續說。

「大學後，唸書變成眾多事情的其中一項，範圍又不像高中那麼固定。所以唸書目標轉變成：在一定的時間內，盡可能唸完最多書。」
「差別在哪？」這不是同一件事的換句話說嗎？
「最佳化問題改變了，要最佳化的是吸收的知識量，限制是一定的時間。大學以前唸不完就不敢睡覺，現在是最多唸到十二點， 唸多少算多少。」孝和從印表機裡拿出一張紙，在背後寫上了

「subject to 後面接的就是限制，要滿足這個限制條件。這稱為『受限的最佳化』（constrained optimization），這兩個問題差別在於， 最佳化的目標跟限制式剛好對調—」

有人遊戲輸掉罵了一聲髒話，孝和被打斷，像當機一樣停了幾秒，接著說：

「給定時間內最有效率的唸書方法，我的經驗是『不同性質的科目交替唸』，才不會因為一直算數學而彈性疲乏。」
「你應該只想唸數學吧。」我盯著孝和諷刺地說。
「如果其他科有數學的一半有趣，我會考慮多喜歡它們一點。」
「竟然對數學做這種噁心的告白……很好，我要學起來。但我的話是喜歡一次唸完同性質的科目。」孝和點頭。

用「圖論」釐清唸書順序

「每個人唸書習慣不同，但我們都同意，存在一種最適合自己的唸書順序。現在，假設一位同學有七科要唸：物理、數學、化學、國文、歷史、地理、英文。他的唸書習慣是―數學前後要接物理跟化學；物理前後是化學、數學，不過物理有很多應用題，所以也可以接著國文唸；化學跟物理類似，前後可以是數學、國文、物理； 國文前後是物理、化學，也可以是歷史、地理；歷史跟地理、國文接著唸，有外國史所以也能接著英文； 地理跟歷史類似，前後可以接歷史、國文、英文；英文則只能接在歷史、地理之間唸。」

「有要求這麼多的嗎！又不是挑食，唸書還有這麼多規矩，在唸書之前他可能得先花上一倍的時間擬定唸書計畫吧。」

我不以為然，孝和在我埋怨的同時低頭畫了一張圖：

「柯南的領結？」

「它叫做『圖論』，是用來表示關聯性的一門數學。」孝和的數青模式要啟動了。
「 圖論緣起於『柯尼斯堡七橋問題』（Seven Bridges of Königsberg）：柯尼斯堡有七座橋，當地居民在橋上散步、遛狗，久而久之，他們好奇能不能在不重複的情況下，一次走完七座橋。」

我又盯著孝和看。他嘖了一聲說：
「不信的話自己上網查。有人拿這個問題問數學家歐拉（L. Euler）。歐拉覺得莫名其妙，他沒去過柯尼斯堡，這也不是數學問題，幹嘛問他。」
「就算是數學問題，我還是覺得莫名其妙。」
「但歐拉很快就發現，他可以『證明沒辦法一次走完』。」

「他去了柯尼斯堡一趟？」 孝和不以為然地冷笑了一聲。
「數學家可以抽象化問題，解決抽象問題，等同於解決了現實問題，根本不需要去柯尼斯堡走一趟。」

「我要是柯尼斯堡鄉民，才不會信一個連走都沒走過的人。」
「真相的存在，並非取決於人們是否相信。」
「再加個風景照，弄個字體，就可以把這句話做成長輩圖了。」我虧孝和，視線回到他畫的圖，每條線段旁邊寫著科目，線段跟線段的交點標上數字。再仔細看，數字剛好是點所連結的線段數目。孝和的聲音從旁邊傳來。

「這個數字稱為度數（degree），歐拉從柯尼斯堡七橋問題發展出圖論這套用點跟線來分析現象的數學領域。在柯尼斯堡七橋問題裡，每一座橋就是一條線。在我們這邊，一個科目就是一條線。線段間的連結則是根據唸書規畫。剛剛的例子是數學要跟物理或化學接著唸，所以你看數學的線段就和跟物理、化學連接。」

我有點意外，兩件完全不同的事情，被數學抽象化之後竟然是相同的。

「德國作家歌德說過：『數學家都是法國人，他們會把你說的話用自己的語言重新講一次，然後就變成截然不同的事情。』」
「我懂歌德的心情。」
「歌德少說了一件事，數學家可以把不同表象的事物，歸納成同一件事情，就像這個例子。所以數學家只要發明一套解決方法， 就可以同時解決很多問題。在這邊，歐拉發現想要一次走完全部的線段，最多只能有2 個點的度數是奇數。超過了，就無法一次走完。」

「規則這麼簡單？」
「還有，奇數點要做為起點。」
我低頭，這張圖只有兩個點的度數是 3，其他都是偶數。我伸出食指，從左邊的 3 出發，物理→數學→化學→國文→地理→英文→

歷史，哎，還真的繞完了。但如果改成從左上的 2 出發，數學→化學→物理，卡住了。

「為什麼啊？」我發問，孝和用問句回答我

「度數是 1 的點會發生什麼事？」
「走進去就出不來了。」
「度數是 2 的點？」
「可以直接穿過去，有進有出。」
「度數是 3 呢？」

我懂了，度數 3 是一進一出，會用掉兩條線，然後就變成了度數是 1 的點。

「起點是『離開不回來』，終點是『進去不出來』，所以可以用度數為奇數的點。其他點就不行。」
「不錯，你這樣跟小昭解釋，她應該就懂了。」孝和補充：「不過要注意，一種敘述可以畫出好幾種不同的圖。」他拿起筆畫了另一種圖。

「像這個同學的唸書習慣也可以畫成這樣，但如此一來奇數點太多，就無法一筆畫走完。簡單地說，敘述跟圖不是一對一（one to one），而是一對多，或是多對多……」

這根本不叫「簡單地說」，我忽略孝和的聲音，趁著圖論的知識還沒忘光光，趕快拿出手機傳訊息給小昭。

本文摘自《超展開數學約會：談個戀愛，關數學什麼事！？》，臉譜出版。

• 文／陳宏賓 │ UniMath 主編、中興大學應用數學系助理教授。

圖論 (Graph Theory) 在數學領域是專門研究一群物件與物件彼此關聯的學問。將要研究的對象物件以頂點視之，兩個物件若有關聯則連接一條邊，圖論主要是研究這個抽象化後由頂點集、邊集所構成的圖的性質。

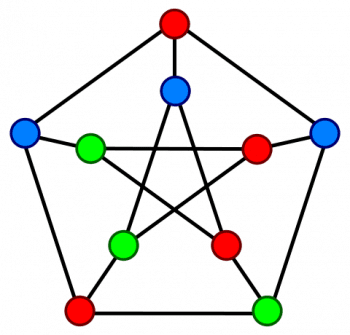
著色問題可以說是圖論最經典的研究主題之一，透過著色，我們可以將圖分類，這個是可以 2 著色的圖，那個是可以 5 著色的圖……。如果有人問你數學家都在做什麼工作？有一個我認為還不錯又簡單的答案，那就是「分類」。各種領域的數學家都在忙著分類，而「著色數」是圖的一項重要分類指標。

讓人困擾60年的《哈德維格-納爾遜問題》

1950 年，就讀芝加哥大學的大學生愛德華 · 尼爾森 (Edward Nelson) 提出了一個困擾數學家多年的著色問題。在二維平面上，任意選一些頂點，如果頂點間的距離是 1 個單位，就把這兩頂點連接一條邊，這種圖稱為單位距離圖 (unit-distance graph)。尼爾森好奇平面上隨便一個這樣子的圖，「點著色數」是多少呢？

「點著色」要求將圖的所有頂點著色，且彼此有邊的頂點必須要塗不同色。而一個圖的「點著色數」就是滿足上述要求的方法中使用最少的顏色數。如果把平面上無限多個點都當成頂點，這個擁有無窮多個頂點和無窮多條邊的圖的點著色數是多少呢？這就是困擾圖論專家一甲子的《哈德維格-納爾遜問題》(Hadwiger-Nelson problem)。

這個問題之所以有名其實是拜已故數學科普大師葛老爹 (Martin Gardner) 之賜，他後來將這個難題寫下來刊載在《科學美國人》，除了吸引不少業餘數學愛好者的目光，也引起不少知名圖論專家的興趣，其中包括了赫赫有名的艾狄胥 (Paul Erdos)。即便如此，集結眾人之力還是沒能完全解開這道難題。不過也不是無功而返，數學家們很快地就將這個涉及到無窮圖的難題的正確答案，限縮到一個乍看不可思議的小範圍──介於 4 到 7 之間。

「開玩笑吧？！一個無窮多個頂點和邊的圖，這麼複雜的圖居然只要最多 7 色就能夠完成點著色。」我想許多讀者心裡會有這樣的 OS，事實就是如此，詳情我們稍後揭曉。

但正確答案究竟是什麼其實還是無人知曉，不過就在今年四月格雷 (Aubrey de Grey) 丟了一篇論文證明：四個顏色不夠用。讓正確答案的範圍又縮小了，只剩下 5、6、7 三種可能。不過，別小看他這一手，雖然看似輕鬆，其實困擾了眾多數學家六十年啊！

而令人感到驚奇的是，突破僵局的格雷教授並不是專門搞數學的，他的身份是一位致力於長生不老的生物學家，某天在玩棋盤遊戲時突發奇想突破了難關。

在此之前，格雷有一項著名事蹟廣為人知，他主張「老化是一種疾病」，只要掌握住關鍵的幾個要素，就能夠抗老，預言人類未來將可以活到一千歲，而且第一個活到一千歲的人已經誕生在世界上了。不論你信不信，我個人希望這件事不要成真，不然五十代同堂可不得了，光是過年吃個年夜飯，連洗碗都有問題啊啊啊！不過，跟秦始皇一樣對於長生不老有興趣的讀者還是參考一下 TED TALK 他的演講《A roadmap to end aging》。

為什麼無限多個點，只要有限個顏色就夠畫了？

其實用最簡單的方式， 9 色就可以順利完成了。理由很簡單，考慮一個邊長 2/3 單位的正方形，最遠的兩點落在對角線的兩個頂點上，簡單利用畢氏定理知道對角線長度不足 1 單位，因此，整個正方形可以塗單一色。接著用 9 個不同顏色的同尺寸正方形，排成九宮格。

再重複把這九宮格平移貼上，規律地鋪滿整個平面就完成了。檢查一下：看看是不是任意一個點，跟距離它 1 單位的點都塗不同色呢？

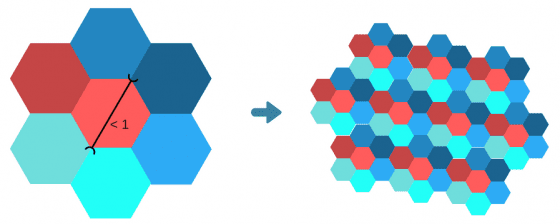
六十年前 7 色的塗法採用類似的概念，只不過用「正六邊形」取代「正方形」來鋪滿整個平面，中間一個加上外圍六個不同色的正六邊形，就是7色的塗法。

那為什麼至少需要 4 色呢？

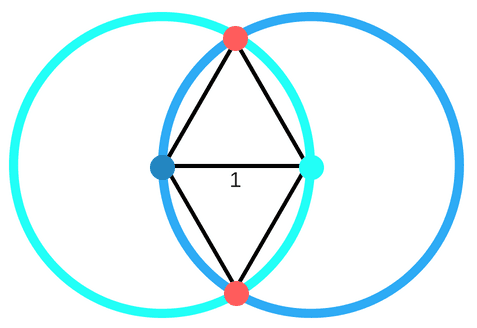
首先畫兩個單位圓通過彼此的圓心，則兩圓心距離為 1，且兩交點距離圓心也是 1，因此光這四個頂點至少要用掉三個顏色才行。

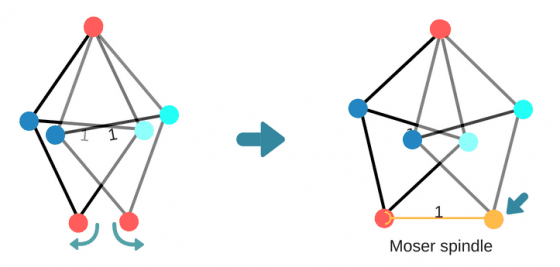
複製中間這個菱形，將兩個菱形的上頂點釘在一起，分別向左右兩邊旋轉，直到下頂點彼此距離為 1 時停止，此時，兩個下頂點的顏色也被迫要相異，因此三個顏色已經不夠用了，不得已只好使用第四個顏色。這個 7 頂點的圖是需要四色的最小範例，由 Leo 和 William Moser 兩兄弟數學家所提出，後來被稱為莫澤圖（Moser spindle）。

格雷帶來的突破

同樣的道理，要證明 4 色不夠用的方法就是找一個至少需要 5 色的例子。格雷受到莫澤圖的啟發，依照三四個步驟，一步一步建構出一個有著兩萬多個點的圖，這個圖無法只用 4 色完成著色。驗證這個反例可不容易，想像光是頂點數量超過兩萬的圖有多複雜，更別說要驗證 4 個顏色夠不夠用。此時，演算法就派上用場，寫個高效率的程式交給電腦處理就行了。

任何一個需要至少 5 色的圖都是這個問題的一項重大進展。數學家希望找到小一點且同樣需要 5 色的圖，最好當然是找到最小的那一種，如此一來就可以更深入地了解究竟需要 5 色的理由是什麼，怎樣的結構會造成顏色數增加，唯有透過不斷地分析解構，才可能更接近真相。格雷也和華裔數學家陶哲軒等人的 polymath 團隊合作，希望藉由團隊的力量將點數大幅度下降。果然，不久後，俄亥俄州立大學的數學家 Dustin Mixon 和 Boris Alexeev 找到一個有 1577 個點的圖。沒多久，德州大學奧斯汀分校的資訊科學家 Marijn Heule 將點數縮小到 874，之後又進一步下降到 826。

一系列的改進給沉寂 60 年的 Hadwiger-Nelson 問題帶來一道曙光。不過，要決定正確答案究竟是多少，恐怕還得需要更多時間才有機會解開謎底，這時候，我心裡反倒暗暗希望格雷的一千歲理論是對的了。

註解：

有人可能會將這個「把平面上所有點著色的問題」跟四色定理那個「把平面圖的點著色問題」搞混；平面圖是指可以把圖畫在平面上讓邊都不交叉。四色定理是在平面圖上著色，而本文討論的不是平面圖。

參考資料：

• Aubrey de Grey, The chromatic number of the plane is at least 5, arXiv:1804.02385v2