史上最多產的數學家，歐拉忌日｜科學史上的今天：9/18

本文與 BOSCH 博世家電 合作，泛科學企劃執行

洗碗，懶人最怕的家務？

你也是個不愛洗碗、不喜歡碰水、碰油污的懶人嗎？

每次吃完飯，光是想到要把碗盤疊一疊端去水槽，好心情就先打了個折。油膩膩的鍋子、黏住的飯粒、髒掉的湯匙……這些小麻煩足以讓人懷疑，自己是不是該多存點錢買台洗碗機？

不過，洗碗機可不只是幫懶人解放雙手的「自動打工仔」。打開它，你其實是在啟動一台縮小版的科學實驗室：「流體力學」幫忙把水柱打到每個死角、「材料科學」讓「石頭」吸濕再吐出熱能、能源工程則在後台幫你精打細算電費。

這些聽起來有點專業的名詞，最後都回到三個簡單問題：碗洗得乾不乾淨？能不能馬上乾爽收起來？花多少電？

第一個痛點：洗碗機的角落，為何會是清潔的法外之地？

使用洗碗機最讓人無奈的情境，莫過於滿心期待地打開，卻發現放在角落的那幾個碗盤，上面還掛著惱人的飯粒或醬漬。明明放在中間的餐具都潔淨如新，為何洗碗機的邊緣角落總是成為水流的法外之地？

科學家透過精密的粒子追蹤實驗，給出了一個物理限制：洗碗機噴射臂的水柱，其實都是「直線前進」的。換句話說，水本身不會自動轉彎，這讓「零死角沖洗」變成了一道難解的幾何學考題。

一次完美的洗淨，必須滿足兩大物理條件：足夠強勁的「力道」以及「零死角的沖洗」。

傳統的「一字形」噴射臂在旋轉時，只能掃描出一個圓形區域，結果就是洗碗機的方形腔體有四個角落，成為水流難以有效觸及的「幾何學死角」。

為了解決這個問題，傳統設計常採用「斜角噴嘴」，試圖將水流送往角落。但研究證實，這種斜角噴嘴會導致水流的「力道」在擊中餐具時嚴重耗損，造成更高的能源消耗與噪音 。

因此，工程師們面臨一個設計上的兩難：是否存在一種設計，能夠在不犧牲「力道」的前提下，從根本上解決「零死角沖洗」這個難纏的幾何困境？

Bosch 的優雅解方 — 以 S 型幾何回應物理挑戰

既然無法改變「水柱是直線的」這個物理現實，那就改變「發射平台」本身的幾何設計。Bosch 所提出的 S 型流線噴水臂，也就是「 360° 水龍捲極勁渦流」技術，便是在這個思路下誕生，其核心優勢在於：

1. 在幾何學上，它減少了死角：傳統一字形噴射臂的掃描範圍是個「圓」，但在 S 型的曲線設計下，噴射臂在旋轉時，其兩端能更有效地深入方形腔體的四個角落與邊緣。這種 3D 噴水方向，使其掃描範圍能完整涵蓋所有洗淨範圍，減少了覆蓋的盲區。
   
2. 在物理學上，它確保了力道：正因為能覆蓋角落，S 型噴水臂減少了對那些低效率「斜角噴嘴」的依賴。確保每一道水柱，都能以接近垂直的角度噴擊餐具，從而最大化「力道」的傳遞效率，達到更佳的清潔效果，同時也更節能、更安靜。

換句話說，這不是單純「水壓加大」的暴力解，而是把流體力學與幾何設計揉在一起的聰明解方。

第二個痛點：為何洗碗機總是烘不乾塑膠餐具？

在各大洗碗機使用者社群中，總流傳著一個共同的謎題：「為什麼陶瓷、玻璃碗盤都乾了，但塑膠餐具或保鮮盒卻總是掛著惱人的水珠？」尤其在台灣這種潮濕環境，碗盤常常像剛洗完澡一樣，水珠掛在上頭，不僅收不了櫃，還容易悶出霉味。

這個現象背後的科學原理，與材料的「熱容量 (Thermal Mass)」有直接關係，也就是一件物體「儲存總熱量」的能力。

我們可以用一個國中物理就學過的熱量公式來理解：熱量 (H) = 質量 (m) × 比熱 (S) × 溫度變化 (ΔT)。

• 高熱容量材料（如陶瓷、玻璃）： 因為密度高、質量重（m值大），它們在被高溫熱水沖刷後，能儲存大量的總熱能（H值高）。洗滌結束後，它們就像一塊塊滾燙的鐵板，能靠自身的「餘溫」將表面的水珠蒸發掉。
  
• 低熱容量材料（如塑膠）： 因為密度低、質量輕（m值極小），即使和陶瓷有著差不多的比熱（S值），它們能儲存的總熱能（H值）依然非常少。熱水一停，表面溫度就迅速下降，完全沒有足夠的「餘溫」去蒸發身上的水珠。

因此，真正的問題不在洗碗機，而在於塑膠材質本身「低熱容量」這個無法改變的物理天性。

那麼，面對塑膠這個難纏的對手，我們是否就無計可施了？如果無法依賴餐具的「內在餘溫」，我們是否能提供一種強大的「外在能量」來逆轉困局？

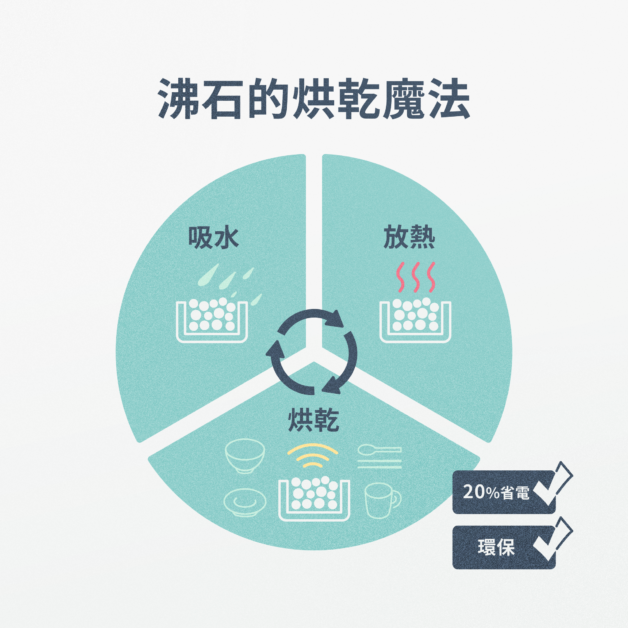
會呼吸的石頭：沸石的烘乾魔法

既然無法改變塑膠餐具「無法儲存足夠總熱量」的內在天性，唯一的出路，就是提供一個強大的「外在熱源」，主動烘乾。

Bosch　的工程師們從材料科學中找到了答案：一種會「呼吸」的天然礦石—沸石 (Zeolite)。

沸石之所以能解決這個難題，是因為它獨特的物理化學特性，能主動為塑膠餐具提供它最欠缺的「外部熱能」。整個過程分為三步：

1. 吸濕 (回收水氣)： 洗滌結束後，腔體內充滿潮濕的水氣。此時，沸石的奈米級微孔結構會像海綿一樣，強力「吸附」這些水分子。
2. 放熱 (創造熱能)： 這個「吸附」的過程，會釋放出大量的「吸附熱」，使得周圍空氣溫度瞬間飆升，同時變得極度乾燥。研究指出，空氣溫度可從約 50.7℃ 提升至 80℃。
3. 烘乾 (熱流循環)： 這股新鮮出爐的高溫乾燥氣流，會被送回腔體內。對於早已冷卻的塑膠餐具來說，這股「外援」熱流循環，正好提供了蒸發表面水珠所需的一切能量。

這就是為什麼有人說，沸石能讓碗盤乾得「比沙漠還乾」。但最讓人驚豔的，並不是它的乾燥能力，而是 Bosch 的工程師如何讓這顆魔法石頭，不像一般乾燥劑那樣用完就丟，可以永續循環。

要重複利用沸石，需要高溫才能「再生」，但誰規定一定要為此額外耗費能源？Bosch 的工程師們靈光一閃：「等等，我們的洗碗機在每次洗滌時，本來就要用加熱器把冷水燒熱，這股強大的熱能，配合適當的密閉空間，不就是現成的烤箱嗎？」

於是，這個絕妙的設計誕生了：在下一次洗程加熱時，「順便」將吸飽濕氣的沸石徹底烘乾還原，而沸石釋放出的水氣，正好直接混入洗滌的髒水中一起排出。根據實測，沸石乾燥能比傳統方式省下約 20% 的電力！更重要的是，省下的不只是錢，也是相對應的二氧化碳排放。
_{*根據博西家電內部實驗室測試結果：沸石洗碗機每次使用耗費約0.76瓦，非沸石洗碗機每次使用耗費約0.98瓦。}

廚房裡的永續實驗室

洗碗機聽起來只是幫懶人偷懶的家電，但細看背後，其實是一座縮小版的實驗室：流體力學解決清潔死角，材料科學讓石頭學會「吸水吐熱」，能源工程則幫你算好電費與碳排。

換個角度想，每一次啟動洗碗機，不只是省下一雙泡在油水裡的手，也同時把高深的科學應用，轉化成日常的乾淨、省電與環保。

下次當你選購洗碗機時， 不妨也從科學家的角度，向它提出兩個關鍵問題：

• 「你如何解決方形空間裡的清潔死角問題？」
• 「你用什麼科學方法來對付濕漉漉的塑膠？」

• 全球銷售第一Bosch洗碗機！
  極致水龍捲 x沙漠極乾燥
  洗得乾淨，乾得徹底
  碗盤永遠保持無痕晶亮的潔淨
• 🥣 全球獨家沸石科技，吸濕放熱密閉烘乾
  🥣 360°水龍捲，全面洗淨死角縫隙
  🥣 75°C高溫水流，Ｓ型流線消滅細菌
  🥣 176件餐具大容量，家庭聚會輕鬆解決
• Bosch洗碗機
  洗淨乾燥殺菌，一次搞定👉https://lihi.cc/idYWT

本文由 德州儀器 委託，泛科學企劃執行。

從 IC 之父 Jack Kilby 在德州儀器發明世上第一顆積體電路，到現在已過了 65 年，而這項科技已經成為我們的日常，並且還在不斷進步。德州儀器不僅是積體電路的先驅者，更長期投資氮化鎵 (GaN) 的電源應用，例如資料中心伺服器電源、再生能源、或是小體積的電源供應器等，開發許多獨創的電路結構。在已到來的次世代半導體浪潮中，德州儀器早已站穩了腳步，成為高壓半導體領域的領導者。

氮化鎵作為新材料的崛起，已成為充電領域的新寵，甚至打敗了傳統的矽 (Si) 基充電頭。然而，要充分發揮氮化鎵的潛力，需要量身定制相對應的策略和戰術。

何謂電路拓樸？電路設計要考量什麼？

拓樸電路是氮化鎵最好的後勤部隊，能讓它發揮 100% 的力量。但這個拓樸電路又是什麼呢？

先來談一下比較陌生的名詞「拓樸」。拓樸是幾何學中重要的概念，主要在研究物體在連續變化下時的不變性質。舉個數學家最愛的例子，就是研究如何把一個帶手把的馬克杯變成甜甜圈。這是什麼鬼題目？這就像問炭治郎什麼時候要開 5 檔，八竿子打不著吧？但對數學家來說，這個題目是可能的，因為帶手把的馬克杯和甜甜圈有個共通特徵，就是有一個洞！只要有這個共同特徵，我們確實就可以透過一系列的數學運算，將馬克杯變成甜甜圈。

舉例來說，漫威電影中班納博士變身成浩克，如果希望浩克的身上能看得出班納博士的影子，就必須用拓樸學先將班納博士的五官這些「特徵」定位好，製作成大家常看到有如網格的 3D 建模，變身成浩克時才不會整個走鐘（台語），臉部比例亂成一團。沒錯，拓樸解決的，是在兩種形狀間切換時，這些特徵與圖案的比例不會隨便亂跑，成為四不像的東西。

回到我們的氮化鎵電路，難道我們要利用拓樸學，把電路板的形狀變成一個甜甜圈或是浩克嗎?當然不是，這邊指的是用更少的元件、更低的延遲與漏電的設計，把相同功能的電路重新改寫配置。

簡單來說，電路拓樸就像是電路板上的藍圖，告訴我們如何把各種電子元件，比如電阻、電容、電感、電晶體等組織在一起，來完成我們想要的任務。

每種電路拓樸都有它的優點和適用的場合。例如，Buck轉換器可以將輸入的電壓降低，適合用在需要較低電壓的應用上。Boost轉換器則可以提升電壓，適合用在需要較高電壓的應用上。LLC轉換器具有高效率和寬輸入電壓範圍的特性，適合用在需要高效率和靈活性的應用上。PFC（Power Factor Correction）則是一種用來提高電源效率的技術，它可以使輸入電流與電壓同步，減少能量損失等等。

然而，這些都是以矽為主的拓樸電路，為了充分發揮氮化鎵百分之百的潛力，我們不能僅僅依賴傳統的電路設計方法和拓樸，而是要重新塑造！

GaN＋電路拓樸=最強？

那麼，我們要如何重新塑造才能全部發揮 GaN 的實力呢？讓我們以一種常見的電路拓樸—功率因數校正 PFC 為例。

PFC，是電路中的交通指揮，負責將電路中電流與電壓同步，以達到最佳的效率。在電訊號經過漫長電路之後，常常導致輸出的電流與電壓波形出現時間差，不再同步。我們知道功率等於電壓乘以電流，因此兩者好好配合，才能發揮最大效益，如果兩者沒有同步，就會降低整體電路的有效功率。

PFC 功率因數修正電路，現在看到在做的事情，就是讓它們好好同步，降低無謂的能量浪費。目前世界各地許多法規都直接要求在電路中加入 PFC，提升用電效率。

那麼問題來了，同樣是 PFC 電路拓樸，現在我們有兩種設計，下方的圖 1－雙升壓 PFC，跟下方圖 2－圖騰柱 PFC。

依照我們希望體積盡可能小的需求，直覺來說你要選哪一個呢？

當然是圖 2，因為他看起來比較簡單嘛。可惜的是，市面上大多矽基半導體的 PFC，都是選擇圖 1 方案。因為圖 2 方案的簡約設計，前提是關鍵的二極體必須具備低的「反向恢復時間」。

所謂反向恢復時間，指的是電晶體在電源切斷的瞬間，電晶體內仍有殘留電荷，會反向放電，造成電路阻塞。而矽基半導體過長的反向恢復時間，會導致電源損耗上升。反之，氮化鎵因為反向恢復時間為零，可以完全適應高效的圖騰柱 PFC。

這邊提到的 PFC 只是氮化鎵的其中一種運用，別忘了，除了零反向恢復時間外，它還有著能承受高電壓與高溫的特性，再加上低漏電率的關鍵被動技能，在目前的半導體戰場上，可說是最強的挑戰者。未來在各種電源供應器上，應該很快都能看見它的身影。

當然，講到這邊，都僅止在題本作答。在實際的晶片設計中，各元件間的距離與電路安排，都需要經過多次的試驗和調整，才能找到最適合的電路拓樸和元件配置，而這也正是德州儀器所擅長的領域。

德州儀器設計出的電源供應器，已經遍佈全世界的重要設備中。除了提供高效的能源供應，節省下的能源，也直接減少了許多碳排。根據估計，對一個 100 MW 的資料中心來說，換上 GaN FET 之後，就算只有提升 0.8% 的效率增益，在 10 年內就能節省多達 700 萬美元的能源成本。尤其在 AI、量子電腦等科技發展蓬勃的現在，在「節流」這一塊的投資，真的非常重要！

看到這鋰，如果你也想訓練這個「黑科技」氮化鎵，打造更強的電路、為世界的節能貢獻一份心力。或甚至像 IC 之父 Jack Kilby 那樣，發展全新的電路架構，做出足以改變世界的創舉，德州儀器歡迎所有熱血人才加入，一起來改變世界吧！

數學家通常都想很多，這是我們的習性。我們會分析對稱或相等這類大家都知道的基本概念，試圖找出更深層的意義。

形狀就是一個例子。我們多少都知道形狀是什麼。我們看到一個物體時，很容易就看得出它是圓形、方形還是其他形狀。但數學家會問：形狀是什麼？構成形狀的要素是什麼？我們以形狀分辨物體時，會忽略它的大小、色彩、用途、年代、重量、誰把它拿來的，以及最後誰要負責歸位。我們沒有忽略的是什麼？當我們說某樣東西是圓形時，看到的是什麼呢？

形狀百百種，可以量化嗎？

當然，這些問題沒什麼意義。就實際用途而言，我們對形狀的直覺理解就已經夠了——生活中沒有什麼重大決定是需要仰賴我們對於「形狀」的確切定義。但如果你有空又願意花時間來想一想，形狀倒是個很有趣的主題。

假設我們現在要思考了，我們或許會問自己這個問題：

這個問題很簡單，但不容易回答。這個問題有個比較精確和有限的說法，稱為廣義龐卡赫猜想（generalized Poincaré conjecture，或譯龐加萊猜想）。這個猜想提出至今已經超過一百年，目前還沒有人解答出來。嘗試過的人相當多，有一位數學家解出這個問題的大部分，因此獲得了100萬美元獎金，但還有許多種形狀沒有找到，所以目前我們還不知道世界上一共有幾種形狀。

動手把形狀畫出來

我們來試著解答這個問題。世界上有幾種形狀？如果沒有更好的點子，有個不錯的方法是畫出一些形狀，看看會有什麼結果。

看來這個問題的答案取決於我們區分形狀的方式。大圓和小圓是相同的形狀嗎？波浪線（squiggle）應該全部算成一大類，還是應該依彎曲的方式細分？我們需要一種通用規則來解決這類爭議，才不用每次都需要停下來爭論。

從幾何學到拓樸學

可用於決定兩個形狀是否相同的規則相當多。如果是木匠或工程師，通常會希望規則既嚴謹又精確：必須長度、角度和曲線都完全相等，兩個形狀才算相同。這樣的規則屬於幾何學（geometry）這個數學領域。在這個領域裡，形狀嚴格又精確，經常做的事情是畫垂直線和計算面積等等。

但我們的要求比較寬鬆一點。我們想要找出所有可能的形狀，但沒時間慢慢區分幾千種不同的波浪線。我們想要的是在比較兩個形狀是否相同時比較寬鬆的規則，它能夠把所有的形狀分成若干類別，但類別的數量又不至於太多。

——本文摘自《不用數字的數學：讓我們談談數學的概念，一些你從沒想過的事……激發無窮的想像力！》，2022 年 9 月，經濟新潮社，未經同意請勿轉載。