「晚安,在幹嘛呢?」
「下週要考試了,都唸不完。」
我(世杰)抬頭看螢幕,遊戲「正在讀取中」的長條圖走到 3/4,心裡閃過一絲罪惡感。
「我也正要準備唸書。」我沒說謊,準備再打五場,三小時後唸書。
開始和小昭用 LINE 聊天後,我發現她很認真,每天都在唸書。如果是別人,我早就虧她「今天有去安親班嗎?」、「不,我不是說打工,是說你去上安親班,繳學費的那方。」但小昭只會讓我自慚形穢,她好上進,我好糜爛,連反省也是在遊戲讀取的空檔。
遊戲開始,MathKing 跟我走同一條路線,那是孝和的帳號。
「她每天都用唸書當藉口來拒絕你嗎?」
「我還沒約!」
我點擊滑鼠,對一隻小兵用了絕招,小兵被炸得四分五裂。
「心虛就算了,不要浪費魔法點數。」
「該怎麼幫助小昭唸書更有效率啊?」
我們在系上的電腦教室。雖然可以在家玩,但坐在旁邊並肩作戰的感覺還是比較好,照我剛剛跟小昭的說法是─—留在系上唸書。
「她沒有接著說『改天可以一起唸』……」
孝和盯著螢幕的臉上露出「怎麼可能」的表情。
「用網路聊天很開心,但人與人深交還是需要見面啊,就像我們要坐在一起打電動。」我嘆了口氣說。
「我們只是說垃圾話比較方便。你們也說垃圾話?」
「我們說情話!見面才能看見表情,知道她說話的時候是微笑、大笑,還是嬌羞。見面才能聽見聲音,知道她的語氣是輕快的,還是不帶情感,又或是害羞。」
「你有病,一直希望對方嬌羞害羞。」我用連續技解決掉敵人,繼續說。「見面才能看見整個人,她的手托腮嗎,還是放在桌上?腿上? 我的手上?」
「這是發花癡,不是在講見面的意義了吧。見面的確有意義, 有更多資訊,就能更了解對方的心思。」

孝和從旁邊突襲,發動範圍技,我們少打多,解決掉三個對手。
「被你說得好像在測謊。」
大概是從我遊戲人物的步伐中看出了沮喪,孝和自以為不著痕跡地安慰我。
「或許她唸書得專心一個人吧。」
「你也這麼覺得嗎!?」
「我們是不是這麼覺得不重要,而是只能這麼覺得。畢竟就算這真的是藉口,你也不能怎樣。哎專心一點!」我的弓箭手角色在會戰時走到最前線,連一發箭都沒射出就領便當了。
孝和對盯著螢幕發呆的我嘆了口氣,說:「不要只會打順手球啊,你應該用數學來一場大逆轉。」
數學唸書術
「唸書其實就是時間管理。大學以前的課業有範圍。作為第一順位,唸書的目標是:用最少時間,學懂該學的知識。得趕快唸完才能去玩。這是一個最佳化問題,目標是時間,限制是要唸的書。」
孝和跟我拉了兩張椅子坐在印表機旁,他繼續說。
「大學後,唸書變成眾多事情的其中一項,範圍又不像高中那麼固定。所以唸書目標轉變成:在一定的時間內,盡可能唸完最多書。」
「差別在哪?」這不是同一件事的換句話說嗎?
「最佳化問題改變了,要最佳化的是吸收的知識量,限制是一定的時間。大學以前唸不完就不敢睡覺,現在是最多唸到十二點, 唸多少算多少。」孝和從印表機裡拿出一張紙,在背後寫上了
「subject to 後面接的就是限制,要滿足這個限制條件。這稱為『受限的最佳化』(constrained optimization),這兩個問題差別在於, 最佳化的目標跟限制式剛好對調—」
有人遊戲輸掉罵了一聲髒話,孝和被打斷,像當機一樣停了幾秒,接著說:
「給定時間內最有效率的唸書方法,我的經驗是『不同性質的科目交替唸』,才不會因為一直算數學而彈性疲乏。」
「你應該只想唸數學吧。」我盯著孝和諷刺地說。
「如果其他科有數學的一半有趣,我會考慮多喜歡它們一點。」
「竟然對數學做這種噁心的告白……很好,我要學起來。但我的話是喜歡一次唸完同性質的科目。」孝和點頭。
用「圖論」釐清唸書順序
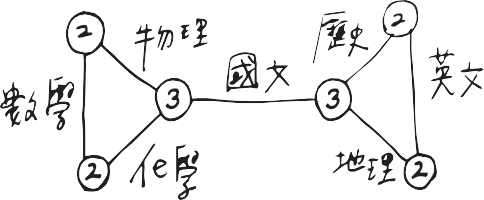
「每個人唸書習慣不同,但我們都同意,存在一種最適合自己的唸書順序。現在,假設一位同學有七科要唸:物理、數學、化學、國文、歷史、地理、英文。他的唸書習慣是―數學前後要接物理跟化學;物理前後是化學、數學,不過物理有很多應用題,所以也可以接著國文唸;化學跟物理類似,前後可以是數學、國文、物理; 國文前後是物理、化學,也可以是歷史、地理;歷史跟地理、國文接著唸,有外國史所以也能接著英文; 地理跟歷史類似,前後可以接歷史、國文、英文;英文則只能接在歷史、地理之間唸。」
「有要求這麼多的嗎!又不是挑食,唸書還有這麼多規矩,在唸書之前他可能得先花上一倍的時間擬定唸書計畫吧。」
我不以為然,孝和在我埋怨的同時低頭畫了一張圖:
「柯南的領結?」
「它叫做『圖論』,是用來表示關聯性的一門數學。」孝和的數青模式要啟動了。
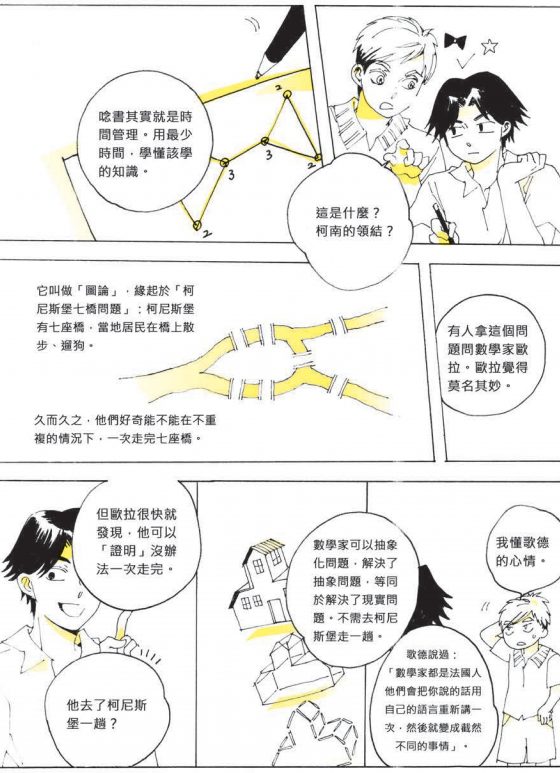
「 圖論緣起於『柯尼斯堡七橋問題』(Seven Bridges of Königsberg):柯尼斯堡有七座橋,當地居民在橋上散步、遛狗,久而久之,他們好奇能不能在不重複的情況下,一次走完七座橋。」
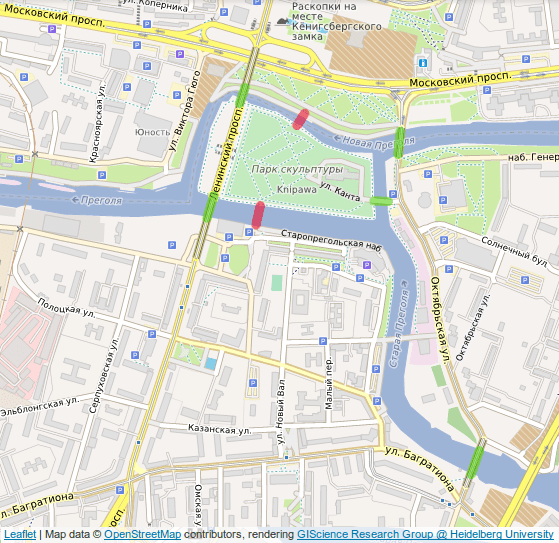
我又盯著孝和看。他嘖了一聲說:
「不信的話自己上網查。有人拿這個問題問數學家歐拉(L. Euler)。歐拉覺得莫名其妙,他沒去過柯尼斯堡,這也不是數學問題,幹嘛問他。」
「就算是數學問題,我還是覺得莫名其妙。」
「但歐拉很快就發現,他可以『證明沒辦法一次走完』。」
「他去了柯尼斯堡一趟?」 孝和不以為然地冷笑了一聲。
「數學家可以抽象化問題,解決抽象問題,等同於解決了現實問題,根本不需要去柯尼斯堡走一趟。」
「我要是柯尼斯堡鄉民,才不會信一個連走都沒走過的人。」
「真相的存在,並非取決於人們是否相信。」
「再加個風景照,弄個字體,就可以把這句話做成長輩圖了。」我虧孝和,視線回到他畫的圖,每條線段旁邊寫著科目,線段跟線段的交點標上數字。再仔細看,數字剛好是點所連結的線段數目。孝和的聲音從旁邊傳來。
「這個數字稱為度數(degree),歐拉從柯尼斯堡七橋問題發展出圖論這套用點跟線來分析現象的數學領域。在柯尼斯堡七橋問題裡,每一座橋就是一條線。在我們這邊,一個科目就是一條線。線段間的連結則是根據唸書規畫。剛剛的例子是數學要跟物理或化學接著唸,所以你看數學的線段就和跟物理、化學連接。」
我有點意外,兩件完全不同的事情,被數學抽象化之後竟然是相同的。
「德國作家歌德說過:『數學家都是法國人,他們會把你說的話用自己的語言重新講一次,然後就變成截然不同的事情。』」
「我懂歌德的心情。」
「歌德少說了一件事,數學家可以把不同表象的事物,歸納成同一件事情,就像這個例子。所以數學家只要發明一套解決方法, 就可以同時解決很多問題。在這邊,歐拉發現想要一次走完全部的線段,最多只能有2 個點的度數是奇數。超過了,就無法一次走完。」
「規則這麼簡單?」
「還有,奇數點要做為起點。」
我低頭,這張圖只有兩個點的度數是 3,其他都是偶數。我伸出食指,從左邊的 3 出發,物理→數學→化學→國文→地理→英文→
歷史,哎,還真的繞完了。但如果改成從左上的 2 出發,數學→化學→物理,卡住了。
「為什麼啊?」我發問,孝和用問句回答我
「度數是 1 的點會發生什麼事?」
「走進去就出不來了。」
「度數是 2 的點?」
「可以直接穿過去,有進有出。」
「度數是 3 呢?」
我懂了,度數 3 是一進一出,會用掉兩條線,然後就變成了度數是 1 的點。
「起點是『離開不回來』,終點是『進去不出來』,所以可以用度數為奇數的點。其他點就不行。」
「不錯,你這樣跟小昭解釋,她應該就懂了。」孝和補充:「不過要注意,一種敘述可以畫出好幾種不同的圖。」他拿起筆畫了另一種圖。
「像這個同學的唸書習慣也可以畫成這樣,但如此一來奇數點太多,就無法一筆畫走完。簡單地說,敘述跟圖不是一對一(one to one),而是一對多,或是多對多……」
這根本不叫「簡單地說」,我忽略孝和的聲音,趁著圖論的知識還沒忘光光,趕快拿出手機傳訊息給小昭。
本文摘自《超展開數學約會:談個戀愛,關數學什麼事!?》,臉譜出版。