根據世界衛生組織的統計,全世界的新生兒中,男嬰與嬰兒總數的比值為 0.515。如果我們單看特定區域或特定國家的話,數值的偏差會更大。墨西哥男女比的比值非常低,而美國與加拿大則高於平均值。然而,在這個人口總數超過七十億的世界,男嬰與女嬰占比的數值應該要相當接近才是。原因很簡單,人類精子帶 X染色體的數量與帶 Y染色體的數量相當,因此就概念上來說,它們的機會均等。這是一個公正的拋擲硬幣遊戲。
別搞混了頻率與結果,每次拋硬幣結果都和前一次無關
拋擲一枚公正的硬幣七十億次後,我們會期望出現正面的機會是一半,但我們是否應當期待看到一百萬個連續的正面出現呢?我們可從一台專門拋擲硬幣的機器得知,儘管硬幣的運行軌跡會受到隨機干擾,硬幣百分之百都出現正面結果的可能性也的確存在。
拋擲一枚公正的硬幣,出現正面的機率是二分之一。從數學理論上來看,我們知道,隨著拋擲次數的增加,「出現正面」與「出現反面」這兩個事件的比值會愈來愈接近 1。以此延伸,可能會誤導人相信上一句的意思表示:如果出現一連串的正面,那麼之後會出現一連串的反面結果來平衡此現象。
我們很容易陷進這樣的謬誤中:如果其中一面很久沒有出現了,那麼它在每一輪拋擲中的出現機會就會增加。儘管我們知道理論上來說,每一次拋擲一枚硬幣,出現兩種結果的機會都完全一樣──硬幣出現正面的機會就跟出現反面的機會相同。人們時常會搞混結果與頻率之間的差別。
「出現一連串的正面結果」是可能發生的。我就曾看過出現非常多次的連續正面結果。直覺上我們會覺得這事件很離奇,但請這麼思考:假設你拋擲一枚硬幣十次,出現七次正面的結果,那麼正面與反面的比例就是七比三。現在,用普遍受到認可的直覺思維來想的話,接續的十次拋擲,出現反面的次數應該要多於六次,以抗衡先前拋擲的結果──超過期望數字的正面次數。但硬幣沒有記憶能力,每一次的拋擲都與前一次無關,只有看著拋擲結果的人會記得先前的紀錄。沒有任何方式可以證明硬幣不可能在接下來的五百次拋擲都出現正面,如果可以的話,我們必定會很驚訝。
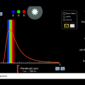
上圖呈現由電腦產生的重複拋擲硬幣五百次後的累積結果(每次出現正面時以 +1 表示,反面以 -1 表示)。水平線代表 0。正面與反面交替領先,「這是一場不分軒輊的競賽」,你可能會這麼想。一般的直覺判斷會覺得擲銅板的圖應該會以零的基準線為軸,上上下下跳動。然而,最常出現的是這類傾向長時間偏向某一端(上或下)的圖。
在硬幣拋出去的那一刻,結果就已經決定了

理論上的絕對隨機與真實、實體世界中的絕對隨機並不相同。儘管對於觀察這過程的一般人來說,那些一開始在壓克力球體中旋轉、決定樂透開獎號碼的乒乓球,確實給出了無法事先預測的數字,但落進洞口的乒乓球並不是隨機產生的。在美式足球開場前,決定由誰開球的拋擲硬幣行為也與「隨機」差之千里。事實上,擲硬幣的結果只是很單純的物理問題;打造一台拋擲硬幣的機器,拋擲任意次數(一千或一百萬次),每一次都出現正面結果──這是辦得到的。
近來設計用以分析拋擲硬幣的實驗顯示,硬幣(甚至是公正的硬幣也一樣)拋擲的結果會傾向其拋擲前的那一面,而這結果取決於硬幣的面以及角動量向量之間的角度。也就是說,硬幣在空中的行進軌跡是由它一開始的狀態所決定。戴康尼斯(Persi Diaconis)、霍姆斯(Susan Holmes)以及蒙哥馬利(Richard Montgomery)打造了一台拋硬幣的機器,透過彈簧裝置的棘輪來拋射硬幣。用這台機器做拋硬幣實驗,一開始正面朝上的硬幣,拋擲的結果總是(百分之百)會正面朝上。這麼一來,擲硬幣的結果便是固定的,而非隨機。只是人們拋擲硬幣的手以及周遭環境中形形色色的變數造成的多樣性,讓結果看起來是隨機的。
然而,在硬幣於空氣中宛如一個緩慢旋轉的陀螺儀進動時,我們可能會被這假象矇騙,以為它實際上是拋擲出去的。硬幣的飛行方向受到其角動量向量決定,可能使它的拋擲結果永遠是正面朝上。所以,一枚一開始就正面朝上的硬幣,如果遵循它既定的軌跡,正面與反面的旋轉固定,拋擲結果可能永遠都是正面朝上。

連續出現同一面很正常,別太驚訝了
如果談的是會受到千里外輕微的地表顫動、或是太平洋上造成騷動的多事蝴蝶而影響的真實拋硬幣事件,情況就不一樣了。但「不一樣」不意味著合理,也不可測。硬幣掉落到地面時,很可能是隨機的,但我們人類對於隨機性的認知,通常會與我們對於隨機結果的預測不一致。因為硬幣的每一次拋擲都與先前的結果無關,所以出現連續一百次的正面拋擲結果時,我們理應不該感到驚訝,但我們卻往往如此。
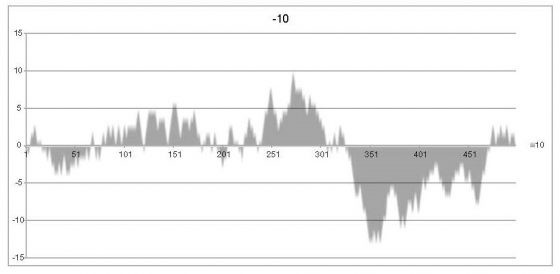
上圖的現象相當詭異。拋擲結果一直跟預期的差不多,直到第四十五次拋擲,反面結果獨領風騷,在接下來的約莫一百零五次拋擲中變得「熱門」!然後,進入了一段合理期,頻頻出現正面結果,使得累積的值接近 0。接著在約莫第二百八十六次拋擲時,再度進到出現大量反面結果的階段。這並不是要說明現實狀況往往違反我們的直覺。
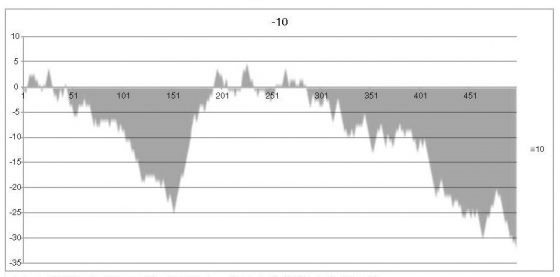
在經過規模大上許多、無法實際操作的投擲試驗後,正面與反面出現次數的實際比值必然會愈來愈接近 1,只是這情況沒有在我們的小規模試驗中出現罷了。拋擲五百次之後,反面出現的次數只比正面多十二次,這似乎是比較接近的數字了,但是連續的反面與正面結果通常可能造成累積結果出現很大的差異。讓我們以下一次的試驗為例。
局面完全倒向正面的結果。累積結果顯示,正面幾乎在整個試驗期間獨占鰲頭,給人留下「怎麼拋擲都不會出現反面」的印象。
大數理論:試驗越多次比率越接近
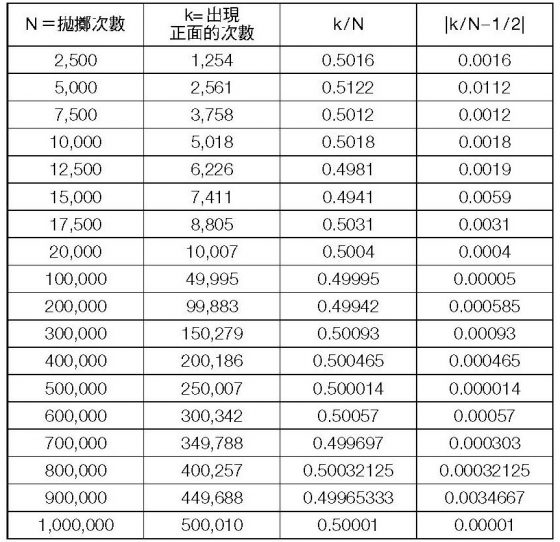
上表是拆解拋擲硬幣一百萬次的結果,這結果是由電腦模擬一百萬次硬幣拋擲的運算而得。比值 k ⁄ N 中的 k 代表成功的次數, N 則代表試驗的次數,這個比值稱為「觀測成功比值」(observed success ratio)。而最右邊欄列出的是「觀測成功比值」與「數學預估的成功比值──1 / 2」之間差異的絕對值。
弱大數法則並沒有排除任何不太可能發生的事件常常出現的可能性,事實上,就算觀測成功比值與數學算出的預測成功比很接近,不保證接下來的試驗也會保持這麼接近的狀態。更為周延一點的數學結果也說明,儘管成功比值很可能朝著數學預測的數收斂,實際的成功值會隨著事件數的增加而發散。這與我們的直覺相違背,但事實卻真的是這樣。
在任何成功機率為 p 的事件中套用弱大數法則,我們可以得知│k / N– p │<ε 的機率會隨著 N 增大而愈來愈接近 1。假設 ε=0.0001(任意選定的),拋擲硬幣的 p =1 / 2,請問│k / N– 1 / 2│小於 0.0001 的可能性會有多大?請注意(見上表),│k / N– 1 / 2│在 N 的值很小的時候是跳動而非遞進的,而 N 的值變大時也一樣。從 100,000 到 200,000,│k / N– 1 / 2│的值是增加的,即便是從 800,000 到 900,000 也是增加的,但在拋擲次數(N)為一百萬次時,│k / N– 1 / 2│的值反而減少。我們誤以為正面和反面的出現次數應該會逐漸接近 0,但這試驗顯示,增加試驗的次數並不會使波動性變得更小。如我們所見,隨著拋擲次數的增加,波動性也變大了。
所以,結論是什麼呢?看起來 N 值愈高就愈不受大數法則約束,因為在難以計量的大數中,有更多讓難察覺的誤差存在的空間。
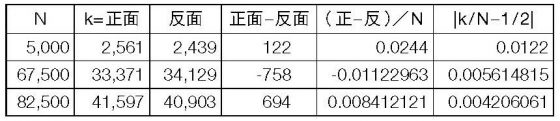
5,000 次的拋擲中,正面出現 2,561 次,反面出現 2,439 次,兩者之間的差距是 122 次。百分之 2.4 的誤差,看起來不算太差勁。但在不知道這些正面的分配的情況下,是可能連續出現 122 次正面的拋擲結果的。從這觀點來思考,想像在 67,500 次拋擲中,也可能連續擲出 758 次反面,或者在 82,500 次拋擲中,連續擲出 694 次正面。也就是說,沒有哪個數學法則能夠在 N 很大的情況下,排除連續出現相當多次正面的機率。
本文節錄自《是湊巧還是機率?巧合背後的數學與迷思》,臉譜出版。

























-200x200.jpg)