文/ 性感的小腳脖 |心理學愛好者、經濟學愛好者,科學人科普作者
買菜、找零、理財、看時鐘……生活中處處有數學,我們從小就能處理與數字有關的問題。那麼,這種數學本領從何而來呢?
數學不用「學」,因為人類本來就會?
哲學家、數學家勒內‧笛卡爾(Rene Descartes,1596~1690)可能會說:它們生而有之。以笛卡爾為代表的理性主義流派認為:人類最初的知識是不「學」自明的,從學習中獲得的知識,要麼不準確,要麼就會誤導人;因此可靠的知識不能來自感覺經驗,而只能來自人心固有的天賦觀念。
對此,不少心理學家紛紛表示認同。他們認為存在一種天生的數學內核(mathematical core),通過自我慢慢發展,這種數學內核最後會「長」成我們所熟悉的一切數學能力 [1]。動物和我們一樣,也擁有數學內核。換句話說,只要發展得當,動物們也能「長」出各種各樣的數學能力來。

長久以來,心理學家都支持「數學天賦論」:數學能力是人類自打娘胎裡出來就有的能力。有些研究發現,10~12 個月的嬰兒已經知道 3 個黑點和 4 個黑點是不一樣的 [2],甚至有研究還發現,剛出生三四天的小寶寶就已經能辨別 2 和 3 的差別 [3]。
除了咿呀學語的嬰兒,大猩猩、老鼠、鳥、貓、海豚、大象等動物也被證明能夠處理數學問題 [4]。無論是繈褓中的嬰兒,還是遠離「世俗」的動物,它們都沒有機會接觸系統的文化和教養,這些證據似乎說明數學能力是一種與感覺經驗無關的天賦。
然而,在數學認知領域深耕了二十多年的拉斐爾‧努涅斯(Rafael Núñez)教授對此表示反對。
努涅斯是加州大學聖地牙哥分校認知科學系教授,近日他在《Cell》旗下期刊《認知科學進展》(Trends in Cognitive Sciences)上發表了一篇綜述文章 [5],系統地總結了 30 餘年來有關「數學能力起源」的論文。在文中,努涅斯旗幟鮮明地反對「數學天賦論」。他表示:
過去之所以將數學能力視為一種不學而能的天賦,是因為混淆了一些與之有關的概念,數學能力沒有天賦,只能是文化的產物。
「數學天賦論」到底有何不對?
人們對數量的識別和辨認,存在兩種通路 [6]。一種被心理學家稱為「數感」(subitizing),它能在一眨眼之間(通常小於 100 毫秒)就完成計數任務,而且正確率接近滿分。但是數感的容量有限,一般只能存在 1~4 個數量。一旦超過 4 個數量,就該另一種通路「大數表徵」(large quantity discrimination)發揮作用了。雖然大數表徵的容量無限,但它的計數能力非常糟糕,不僅慢而且不準確。
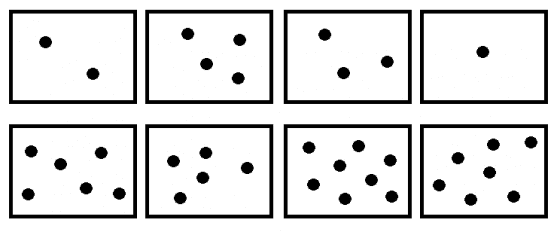
舉個例子,在下圖第一排中,我們一眼就能看出每個方框中各有多少黑點,這是數感作用的結果;然而,第二排就很難一眼看出來了,如果硬要用眼睛看的話,那麼我們只能得到一個近似的答案,這就是大數表徵。
通過總結,努涅斯教授列舉了數學天賦論的三大問題:
首先,數學天賦論帶有明顯的目的論(teleology)色彩。所謂目的論是指,對現象的解釋是依據它的用處,而不管它的內在形成過程是什麼樣。比如說,目的論認為人之所以有眼睛。是因為人要看東西,而不是因為有了眼睛所以人才能看見東西。數學天賦論對數學能力的解釋正是如此:因為數學在生活中能提高人和動物的生存優勢,所以大自然才選擇了它。
但是,作為數學能力生物前提的數感和大數表徵,並不能單獨形成完備的數學能力,後者必須在語言、符號等文化因素的「催化」下才能實現。努涅斯用滑雪運動做了一個類比,身體平衡和直立行走能力都是滑雪的生物前提,但不能因為身體平衡和直立行走是自然選擇的產物,我們就說滑雪技術也是一種天生的本領。
其次,數學天賦論忽視了原始社會居民的情況。目前的研究大多是以現代社會居民作為被試(特別是大學生),他們在實驗中展現出了豐富多彩的數學能力。然而,原始社會居民的數學能力卻十分匱乏。不像現代人的數學系統能表示 10 個以上數量(比如中文能數到 10,英語能數到 12),絕大多數的原始部落居民只能表示 5 以下的數量,更有一些部落的數學系統中只有 1 和 2。這就說明,離開了現代社會這個大環境,人類的數學能力還僅僅停留在最原始的水準上。因此,原始社會中所缺少的文化因素,一定是數學能力發展的必要條件。
最後,努涅斯認為當前動物研究的結果也存在過度推廣。那些能在實驗中展示數學才能的動物們,都接受過特別的訓練。努涅斯在文中就列舉了一項研究,為了學會識別簡單的數字,猴子們學習了近四個月,嘗試了 2 萬餘次,即使這樣,它們的準確率也只能達到 75%。而且,實驗室環境也經過了精心佈置,有很多細節都有利於動物們表現數位能力。然而,大自然中的動物從來沒有接受過訓練,它們的生活環境也沒有任何人為因素。因此,實驗室中的動物在多大程度上能代表全體動物們呢?這要打上一個問號。或許我們只能說,實驗室中的動物才具有數學能力。

會區分多跟少,不表示你會數學!
努涅斯表示,心理學家過去對於「數學來源於天賦」的誤判,可能與他們濫用名詞有關。努涅斯特別強調了「數量」(quantitative)與「數字」(numerical)的不同,前者指簡單地感知到不同數量之間存在區別,而後者則是借用符號進行更為抽象的運算。
說白了,心理學家所認為的我們與動物共有的數學能力,應該叫做「數量能力」,它是一種更接近知覺層面的現象,就像我們能感知物體的大小、顏色、方向一樣。努涅斯認為,心理學家將這種知覺現象混淆成了數學能力,他們經常引用的證據,說嬰兒和動物也能區分不同數量,這其實是一種天生的知覺現象,與數學無關。因此,能夠區分「少」和「多」之間的差異,並不能說是掌握了數學能力。只有在經過語言和符號的轉化後,這種知覺現象才能進一步發展為我們現在稱之為數學的那種能力。

靠先天還是靠後天?該學還是得學呀!
「數學能力是文化的產物」,努涅斯的觀點一發出便引起了爭議。
同一期的期刊上還刊登了德國圖賓根大學動物心理學家安德里亞斯‧尼德(Andreas Nieder)的反駁短文 [7],他認為數學是大腦的產物,而大腦的生長模式早已由基因「預設」,因此數學只能是天生的。雖然大腦有可塑性──大腦隨環境變化而發生改變,但尼德認為這種可塑性的影響微乎其微,因此文化對數學並沒有多少干涉能力。
這兩位同行之間的爭論還在繼續,但無論數學能力是先天還是後天的產物,該學的數學還是要學啊!
參考文獻
- Wynn, K. (1998).An evolved capacity for number. In The Evolution of Mind (Cummins, D.D. and Allen, C., eds), pp. 107–126, Oxford University Press.
- Antell, S. E., & Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Dev, 54(3), 695-701.
- Strauss, M.S. and Curtis, L.E. (1981) Infant perception of numerosity. Child Dev. 52, 1146–
- 楊偉星, 張明亮, 李紅霞, 楊雅琳, &司繼偉. (2017). 人類基本數學能力的進化證據. 心理科學進展, 25(5), 810-824.
- Núñez, R. E. (2017). Is there really an evolved capacity for number?. Trends in Cognitive Sciences, 21(6).
- Mandler, G., &Shebo, B. J. (1982). Subitizing: an analysis of its component processes. Journal of Experimental Psychology General,111(1), 1-22.
- Nieder, A. (2017). Number faculty is rooted in our biological heritage. Trends in Cognitive Sciences, 21(6), 403–404
本文版權屬於果殼網(微信公眾號:Guokr42),原文為〈数学能力是人类固有的天赋?有人不这么看〉,禁止轉載。如有需要,請聯繫sns@guokr.com。