- 作者/大衛.翁弗拉許;譯者/林柏宏
孕育學術研究的亞歷山卓圖書館
在古代,月亮催生了天文學,天文學催生了科學整體。
到了西元前三世紀,科學研究集中在埃及的亞歷山卓,創建這座城市的是來自馬其頓的亞歷山大大帝(Alexander of Macedon,西元前 356-323),他支持科學研究,而他最信任的將軍托勒密一世(PtolemyI Soter,約西元前 367-282)亦然。托勒密後來成為埃及的統治者,創建了一個王朝,王位一直傳到著名的埃及豔后(Cleopatra VII,西元前 69-30)。

在位的四十一年間,托勒密監督著一座巨大研究中心的建造,也就是亞歷山卓謬思宮(Museum of Alexandria)。建築工程在托勒密之子托勒密二世(PtolemyII Philadelphus,在位時間西元前 285-246)統治下繼續,最後造就的場所內有實驗室、關著異國生物的籠子、一座存放屍體的醫學院、來訪學人的起居空間,並提供王室聘任常駐學者所需的協助。
謬思宮與一座圖書館相連,首批館藏便是從雅典運來的亞里斯多德藏書。
亞歷山卓圖書館與謬思宮經歷興衰起落,持續營運了約六世紀之久,在托勒密二世與托勒密三世(在位時間西元前 246-222)時期,學術研究最鼎盛。在這段托勒密時代的初期,藏書規模大幅增長,估計有五十到一百萬卷書。那時候極為重視蒐羅書冊,亞歷山卓的警員甚至負責搜查入港船隻,一旦找到新書就送回圖書館,讓抄寫員在莎草紙上謄寫複製,供學者取閱。
圖書館裡的學者包括幾何學家歐幾里得,以及各式各樣的天文學家、物理學家與數學家,如埃拉托斯特尼、阿基米德與後來的克勞迪亞斯.托勒密(Claudius Ptolemy, 約 100-170), 這些人對月球的科學研究都做出了關鍵貢獻。
圖書館還接待了一位愛奧尼亞學者,這個人結合幾何推理與精密觀測,大大改變了未來幾世紀天文學的發展方向,讓月球登上主角。他名叫阿里斯塔克斯,接下來我們要來講他的故事。
阿里斯塔克斯測量出月球的直徑與距離
月球在希臘化時代成了研究重點,無論是測量它本身的體積、與地球之間的距離,抑或是計算地球與太陽的距離、這三個天體之間的相對大小,月球都是不可或缺的要角。薩摩斯島的阿里斯塔克斯是以上這些工作的靈魂人物。
薩摩斯島位於愛奧尼亞地區,阿里斯塔克斯懷抱著愛奧尼亞式求知傳統,透過觀察自然求取解答。雖然出生於薩摩斯島,他卻在亞歷山卓受教育,生存年代正好是托勒密王朝前三任君主在位時期,也難怪他想留在這個埃及大都會,以便利用龐大的圖書資源與謬思宮的設備,並取得資助研究者的獎助經費。
希臘人追尋可詮釋宇宙的物理模型,巴比倫人使用量化方式進行測量,而阿里斯塔克斯是史上第一位結合這兩者的人。
從這種觀點出發,他產出了一連串洞見,將月球推入天文研究的鎂光燈底下。阿里斯塔克斯的深刻見解之一是,測量月食開始後,月亮要經過多久才會暗下來,以及昏暗維持了多久,這麼做其實已經是在測量相對於地球陰影的月球體積了,並藉此得知地球直徑大約是月球的 3.5 倍。
既然日食是因為從地球所見的月球最大剖面剛剛好勉強遮住太陽剖面,阿里斯塔克斯也明白了如何按比例縮減遮擋的影響。只要在面前拿著一枚有一定直徑的硬幣,在一定距離中,這枚硬幣就可以完全遮住一輪滿月,與月球遮住太陽的道理相同。
阿里斯塔克斯畫出圖表後,利用簡單的幾何推算出月球與我們之間的距離估計有月球直徑的三十五倍或地球直徑的十倍。對照今日的測量結果,這只有實際長度的三分之一,但就一個只用擺在眼前的硬幣充當測量工具的研究者來說,能算到這樣真是相當了不起。更了不起的是,阿里斯塔克斯的天才使他懂得運用月球相關知識來求得從地球到太陽這麼遠的距離全長。
弦月與日心說
讓阿里斯塔克斯受到後世紀念的地球繞日宇宙模型累積了好幾項發現才開花結果。
從他畫的月球、地球與太陽的相對直徑比較圖可看出他的幾何推理,可惜保留至今的圖表沒能展現他最偉大的見解:當月球呈現弦月時,地球、月球與太陽正好會形成一個直角三角形。
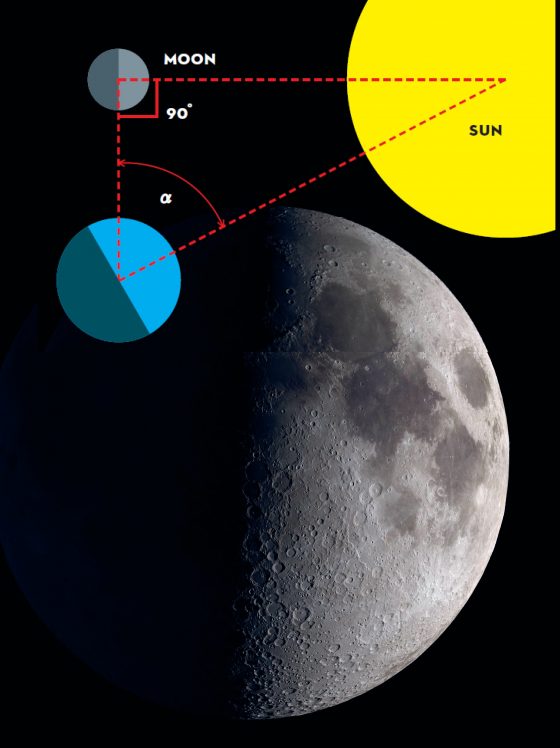
遇到弦月時,阿里斯塔克斯會開始測量自地球中心射出、分別通向太陽與月亮的兩條直線所夾的角度,測量結果可確定地球到太陽距離和到月亮距離的比例。他利用簡略的幾何方法就抓出了這個比例,發現前者是後者的十八到二十倍。
我們現在已知,地球和太陽的實際距離與到月球距離相比幾乎是四百倍,所以阿里斯塔克斯誤差了二十倍,但這是因為他的角度測量不夠精細,量成了 87 度,實際夾角應為 89 度 51 分。
因此可以說,阿里斯塔克斯的方法是恰當的,如何應用觀測結果的推想也是合理的。如果太陽看起來和月亮一樣大,離我們的距離卻是月球的二十倍,那麼太陽的體積約是地球的六倍。
阿里斯塔克斯認為,一顆這麼大的太陽繞著地球轉似乎挺荒謬的,然而在一百年前,亞里斯多德已經思考過並拒絕了以太陽為宇宙中心的理論,理由是沒有人觀看星星時會出現視差,要是地球在太空中移動,顯然看到的星星也會動才對。
由於沒人見過恆星視差(stellarparallax,星星顯現出的位置改變),亞里斯多德於是說,星星必須遠得難以想像才會如此。阿里斯塔克斯對此回應,星星的確離我們難以想像地遙遠,他主張,正由於這麼遠,這些星星本身一定也像太陽一樣─ 大概就是像太陽,有它們自己的行星與生命形式。
埃拉托斯特尼計算地球圓周長
阿里斯塔克斯計算地球到月球距離和地球到太陽距離時,並未算出確切長度,只求得比例。他估算地球到月亮的距離為地球半徑的二十倍,而地球到太陽的距離是這段間距的十九倍,也就是三百八十段的地球半徑長。
要將這些比例轉化成確定的長度,以揭示月球實際體積與它到地球的距離,就得有人量出地球的大小。完成這任務的是埃拉托斯特尼,一個和阿里斯塔克斯一樣、任職於亞歷山卓圖書館的人。

埃拉托斯特尼是館長,因職務之便擁有大量的時間讀書。他的任期正是圖書館與相連的謬思宮蓬勃成長的時期,書冊從他們已知的世界各地持續輸入。
埃拉托斯特尼從館中一本書裡讀到南方有座城市,塞耶尼(Syene,現稱為亞斯文〔Aswan〕),那裡有一口深井,夏至當天正午時分,陽光直射可深入井底,不會切出任何陰影。於是,埃拉托斯特尼利用亞歷山卓城某座塔夏至當天的影子長度,算出了兩座城市之間在地表上的弧度,得到的結果是圓的五十之一。也因此,地球圓周會是亞歷山卓到塞耶尼距離的五十倍。
為了求得這段距離,埃拉托斯特尼可能雇用了勘測員進行測量,不然就是他知道前往塞耶尼的駱駝商隊以特定速率行進大概要花五十天才會抵達,依此為估算根據並求得距離。那個時代的希臘人也可以使用一種阿基米德剛剛發明的里程量表。
總之,不管用哪一種方法,埃拉托斯特尼求得兩座城市相距只有 5,000 斯塔德(Stadion),以此推算,地球圓周長就是 252,000 斯塔德。(1 斯塔德即是一座運動場長度,但運動場有好幾種。)如果埃拉托斯特尼是取長度最短的運動場當作距離單位,那麼計算結果就得到地球最大圓周長為 39,564 公里,只比真正的長度少了一點點。