文/黃大維|目前在台灣大學就讀統計碩士學位學程。我的研究領域是特徵表達與降維分析、序列決策模型、以及財務時間序列,我喜歡用商業的觀點切入大數據與資料科學!
最近在泛科學上看到一篇非常精彩的文章〈p 值的陷阱〉,是在談論「p 值」在研究上的問題,其實看完之後滿有感觸的,儘管 p 值是個在初等統計學就會談到的統計量,但大部分的學生(甚至某些研究人員)學完後只記得:p 值 < 0.05 的話就拒絕虛無假設。因為這個條件非常簡單好記,而且大多數的統計軟體都會報告 p 值,所以不少人會直接看 p 值就做出結論。
P 值的陷阱系列
其實 p 值本人是相當無辜的,美國統計協會(American Statistical Association, ASA)在 2016 年的聲明中提到一段有趣的對話:
Q: Why do so many colleges and grad schools teach p = 0.05?
A: Because that’s still what the scientific community and journal editors use.
Q: Why do so many people still use p = 0.05?
A: Because that’s what they were taught in college or grad school.
坦白說,p 值的誤用本質上可說是因為「教學」本身出了問題。我一直到大四為止也都覺得 p 值 <0.05,拒絕虛無假設,世界圓滿,現在看到許多學弟妹作分析,也會直接寫「p 值 <0.05,拒絕虛無假設,資料證明了 A 因子是 B 結果的重要原因」,其實這樣的推論是非常危險的。所以,我決定了寫一篇介紹 p 值的文章。
假設檢定:Neyman-Pearson Paradigm
在探討 p 值的意義前,我們必須先了解假設檢定的基本精神。現在有一個統計模型(這個模型就是真理),裡面有個參數 θ,傳統統計的目標是希望去「推論」參數 θ 的性質,比如說:θ 的值為多少?(估計)現在有個假設/宣稱是 θ 落在某個區域 Θ,θ ∈ Θ,根據蒐集的資料這個假設是不是正確的?(檢定)
所謂的假設檢定(Hypothesis Test)便是如上所說:有個假設(hypothesis)是「參數 θ 落在區域 Θ,θ ∈ Θ」,希望根據蒐集到的資料,驗證上述假設的真實性。我們稱「參數 θ 落在區域 Θ, θ ∈ Θ」這個假設被稱為虛無假設(null hypothesis,H0),也就是無中生有的假設。
同時,也有對立假設(alternative hypothesis,H1),是與虛無假設完全相反的假設,也就是「參數 θ 並不落在區域 Θ,θ ∉ Θ」。因此,真實情況下只有兩種可能,「H0 為真」或是「H0 為假」。同時,我們觀察資料後也只能得到兩種結果:「資料有充分證據證明 H0 為假」以及「資料沒有充分證據證明 H0 為假」。
在假設檢定中有三個重要的要素:統計模型(真理)、虛無假設、資料。舉個例子吧!有一個好事者說:「大鼻長得帥。」大家當然會想要問:你憑什麼這麼說?有何證據?因此,好事者就說:好吧!那我就來隨機問問台北市的路人大鼻帥不帥,把第 i 個人的回答紀錄成 Xi,假設全台北市的人中覺得大鼻帥的人的比率為 θ,如果有超過 50% 的人說大鼻帥(也就是 θ> 0.5),如此一來我們就可以進行假設檢定了:
- 統計模型:Xi~Bernoulli(θ),其中每個人的回答都是獨立的。
- 資料:隨機詢問 100 個台北市的路人,蒐集到了樣本 ( X1, …, X100 )。 。
- 假設:H0: θ ≤ 0.5 (虛無假設為大鼻不帥,好事者想利用資料去證明虛無假設不是真的)。
在假設檢定中,我們可以考量兩個維度,其中一個維度是「真實情況下虛無假設是否為真」,另一個維度則是「根據蒐集來的資料,是否拒絕虛無假設」,由此我們可以得出在進行假設檢定時會有以下四種情況:
由於每一次抽出的樣本都會不同,比如說:好事者每天遇到的 100 個路人應該都不一樣,我們沒辦法保證每一次抽出的樣本都能反映出真實情況,因此在進行假設檢定時可能會犯兩種錯誤:
- 第一型錯誤(Type I Error):虛無假設為真,樣本卻顯示我們應該拒絕虛無假設。
- 第二型錯誤(Type II Error):虛無假設為偽,樣本卻顯示我們應該接受虛無假設。
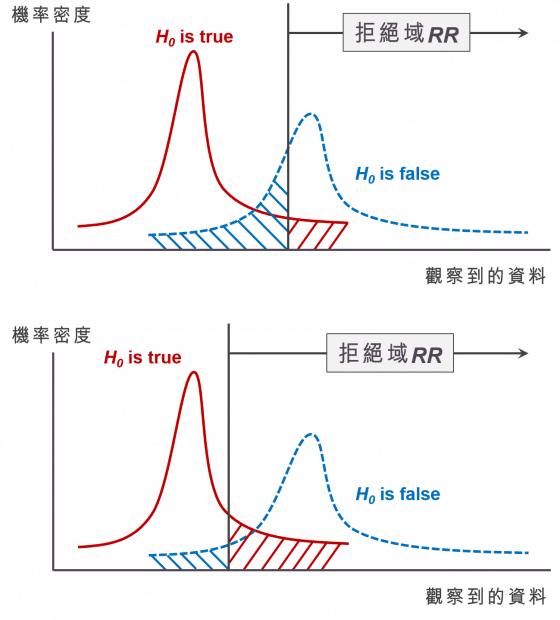
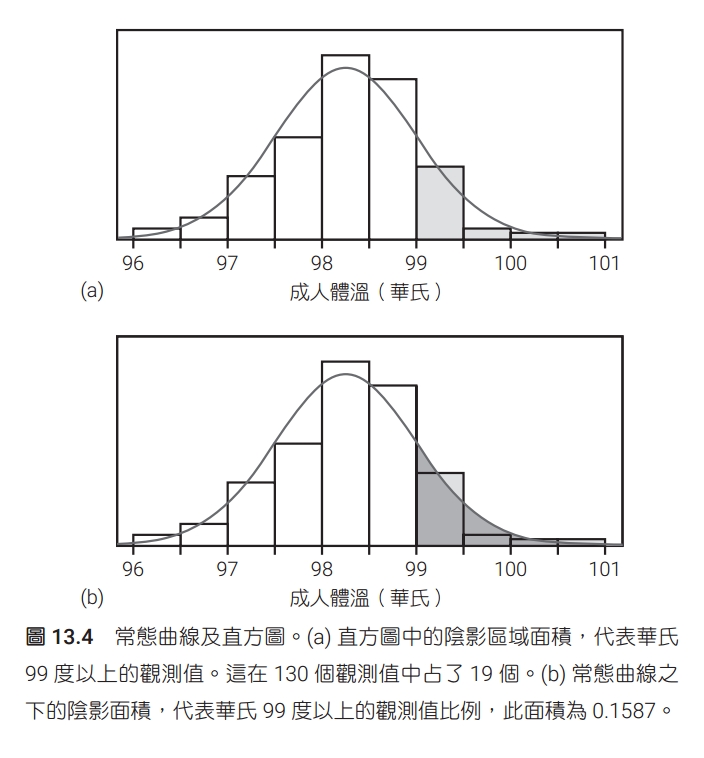
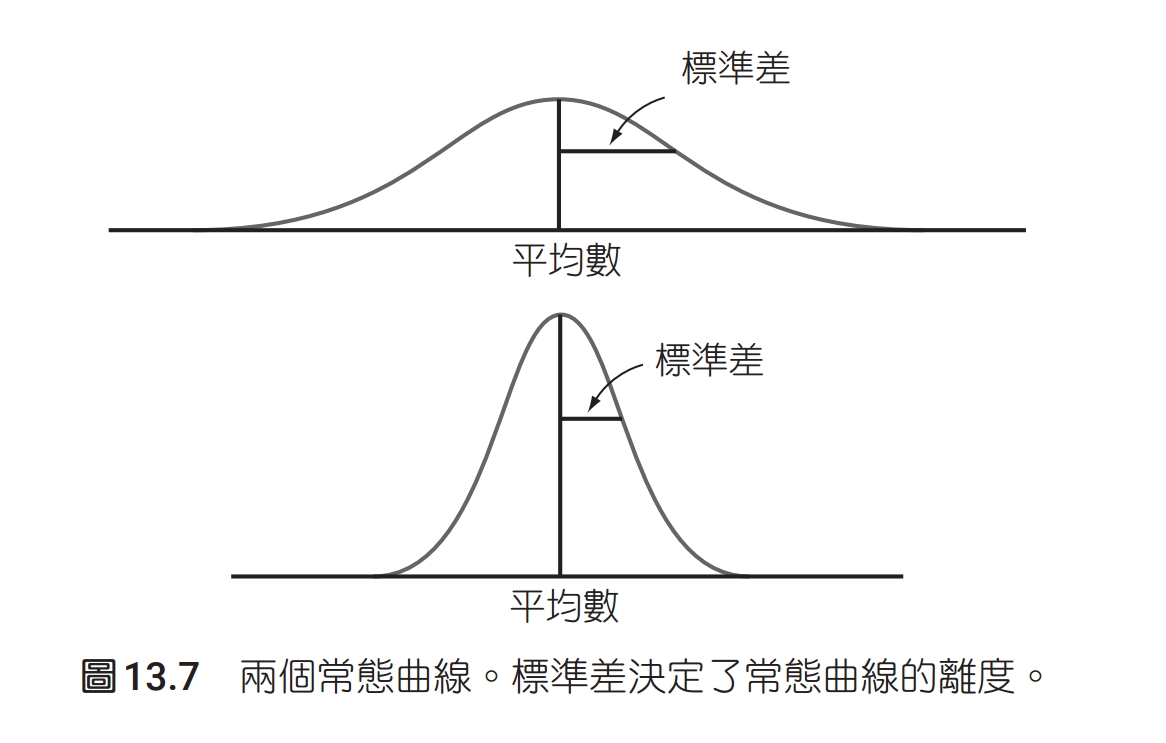
理想上,我們希望能夠讓第一型錯誤與第二型錯誤的機率越低越好,最好都是 0,但假設檢定的天性,使得這件事無法發生。如果我們希望第一型錯誤發生的機率比較小(上圖紅色區域的面積),代表我們應當將「拒絕虛無假設」的標準訂得更嚴格一點(拒絕域比較窄),才不會一不小心就拒絕了虛無假設。然而,這麼一來就有可能在虛無假設為假的情況下,仍然不拒絕虛無假設,也就是第二型錯誤發生的機率(上圖藍色區域的面積)變高了!反之,如果我們希望第二型錯誤發生的機率比較小(下圖藍色區域的面積),代表我們應當將「拒絕虛無假設」的標準訂得寬鬆一點(拒絕域比較寬),但這樣一來第一型錯誤的機率(下圖紅色區域的面積)就會上升。
在第一型錯誤與第二型錯誤的機率存在抵讓(trade-off)關係時,統計學家決定:不如我們先限制其中一項錯誤的機率,再去看看要如何找出拒絕的標準,使得另一項錯誤發生的機率越低越好。因此,在進行假設檢定時,我們的首先會確保第一型錯誤的機率不超過一個很小的數值 α,一般習慣將 α 訂為 10%、5%、或是 1%(只是習慣),確保第一型錯誤發生的機率很低。接著,我們找出一個拒絕的標準,使得第二型錯誤發生的機率越小越好。通常,我們將「拒絕虛無假設的標準」寫成一個區域的型式,稱為拒絕域 RR(rejection region),當我們蒐集到的樣本落於拒絕域 RR 時,我們便拒絕虛無假設。
因此,當第一型錯誤的機率 P( X1, …, X100 ) ∈ RR∣H0 is true) ≤ α 被 α 控制住後,我們就可以依照某些方法,計算出實際得拒絕域 RR。一旦拒絕域決定了,我們便可以計算出第二型錯誤的機率 β = P( X1, …, X100 ) ∉ RR∣H0 is false)。此時,我們將一個假設檢定的檢定力(power)定義為 1- β。統計學家期待能夠在控制住第一型錯誤發生機率的情況下,得到一個拒絕域 RR*,使得第二型錯誤發生的機率最小,也就是使得檢定力最強。這樣利用 α 控制住第一型錯誤的方法,就是所謂的 Neyman-Pearson Paradigm。而針對給定的虛無假設,「拒絕域為 RR*」的檢定方法,就稱為「最強檢定力檢定」(most powerful test)。
P 值:幫助我們決定是否拒絕 H0 的好工具
前面講了一大串都沒有談到 p 值是什麼,現在終於要開始了!P 值最早是在 1900 年在 Pearson卡方檢定的論文中被提出的(皮爾森大大真是了不起 RRRR),其實 p 值本身有一個更一般化的定義,但在這裡我用的是平常我們看見的 p 值的定義。
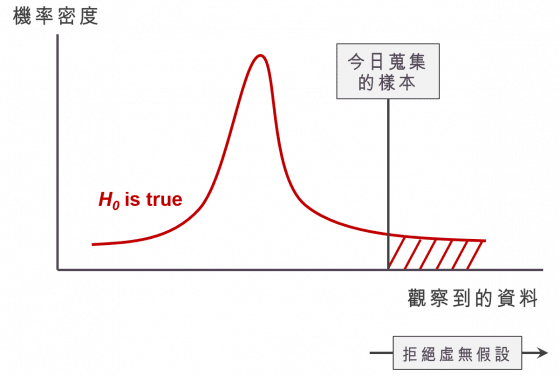
假設現在好事者已經問完 100 個路人,得到了一組樣本。p 值的定義是,「在虛無假設為真的情況下,如果好事者明天再去蒐集一次樣本,得出的新樣本比目前的樣本更能拒絕虛無假設的機率。」
大鼻阿,你到底在說什麼啊…… 讓我來畫個圖跟大家說明。在下圖中,資料越靠近右邊,代表拒絕虛無假設的傾向越強,而灰色的線是今天好事者抽到的一組樣本,紅色的曲線是在虛無假設為真的情況下,樣本的機率密度(probability density),那麼落在這組樣本右手邊的紅色面積,就是所謂的 p 值:在做一次調查,得到一組與目前資料相比,「更傾向拒絕虛無假設」樣本的機率值。
如果我們得到的 p 值很小,就代表著:目前這組樣本拒絕虛無假設的傾向已經非常強了,幾乎不可能再得到更傾向於拒絕虛無假設的樣本了,因此 p 值只要夠小,我們就可以拒絕虛無假設。
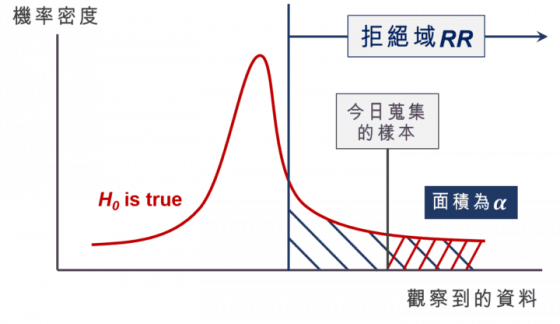
這時我們很自然會想問,p 值到底要多小,才算是夠小呢?其實我們可以 p 值跟 α 來比較,下圖中資料落於拒絕域的機率(藍色區域面積)為 α,我們可以很清楚的看到如果 p 值(紅色區域面積)比 α 還小,就代表今天蒐集到的樣本落於拒絕域。這就是為什麼我們常說 p 值 < 0.05 就拒絕虛無假設的原因。
小結:定義有說的才能,沒說的就不能
在大家了解 p 值的定義之後,我們就可以來看看美國統計協會的聲明中提供的 p 值使用指引:
P-values can indicate how incompatible the data are with a specified statistical model.
大家如果只單看這句話,可能會覺得「p-值可以用指出實際資料與預設統計模型的差異性」,但如果仔細看 ASA 文章裡的敘述,會知道「預設統計模型」是指「虛無假設為真情況下的統計模型」。
P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
聲明中提到,p 值並不是用來衡量「虛無假設不為真」的機率,若硬要談到「虛無假設不為真」的機率,其實要嘛是 1 (虛無假設不為真),要嘛是 0(虛無假設為真),p 值用來衡量的是在虛無假設為真的情況下,我再重新蒐集樣本,新的樣本比現有樣本更能拒絕虛無假設證據的機率。
Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
從來每有一個統計學家會說,只要 p 值 < 0.05(或可說是達成統計顯著),就天下太平了。 p 值只是眾多統計指標中的一個衡量方法而已,如果在最初設計統計模型時就設計錯了,而沒有去檢驗最初模型設定的合理性,那麼 p 值 < 0.05 甚至會為你帶來一場災難!
Proper inference requires full reporting and transparency.
對於統計這麼學問掌握純熟的人,其實說到底很容易去「操弄 p 值」,說到底這是一個非常糟糕的行為,但就跟小時候做實驗掰數據一樣,很快就能產生好結果。真正要驗證一個理論的正確性時,是需要做許多不同的統計測試的,像是財務界頂尖期刊 Journal of Finance 裡面的統計驗證方法就非常嚴謹,值得效法。
A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
在迴歸裡面,我們時常會去檢定一個解釋變數的係數是否為 0,有些人會覺得 p 值越小代表這個變數越重要,錯!其實只要你的樣本數大一點,任何的解釋變數係數是否為 0 的檢定都很容易得到足夠小的 p 值。有興趣的朋友可以看看這一篇論文,有詳細解釋大樣本時 p 值的問題。
我自己習慣是,假設現在有 30 萬個資料,我可能會從裡面隨機抽出 10,000 組樣本數為 100 的小樣本,然後在每個小樣本上去跑回歸,看看 p 值 < 0.05 的比率有多高,但我不確定這個手法有沒有很嚴謹的統計證明,如果有朋友有方法的話還請告訴我!
By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.
簡單來說,其實 p 值並不能完全代表真實資料與模型之間的差距,仍然需要進行更縝密的資料分析才能做到品質比較高的統計推論。其實很簡單,如果只是看看 p 值就萬事大吉,還要這麼多統計學家幹嘛 XD
希望大家看完這篇文章,有更了解 p 值的本質。 P 值本人是相當無辜的,而且也從來沒人說 α = 0.05 是真理,需要依據你的問題與蒐集到的資料,來判斷 α 應該要落在哪個水準比較合理。在抨擊 p 值本人前,要想想世上無完人,他能夠做的就是他的本分,不要再逼迫已經年齡過百的他了 QAQ
本文轉載自作者部落格「大鼻觀點」,喜歡他的文章也可以追蹤同名臉書粉絲專頁。