身為一名訓練師,你真的了解你的寶貝們嗎?寶可夢圖鑑讀熟了沒?
其實圖鑑告訴你的比想像中的還多喔!每個星期周末跟著 R 編一起來上一門訓練師的科學課吧!來跟大家分析這些寶可夢們是如何使用科學力來戰鬥的。

體重成謎、上山請小心#76 隆隆岩
雖然標題只寫著隆隆石,但這一個「小拳石–隆隆石–隆隆岩」的石頭三人組值得更多檢視。因為當我一如往常在檢視每一隻寶可夢的基本數據時,馬上遇到了一個……不~三個問題。
沒錯~又是身高體重出事了。
圖鑑中,這三隻神奇寶貝的數據如下:
我們先假設牠們都是一顆完整的球體,以方便計算牠們的體積(註1),並直接以牠們的體重除以體積來求密度。你覺得這些數據看起來很正常嗎?
別說一般岩石的密度 2,515 kg/m3 了,我們的石頭三人組中密度最大的小拳石才只不過比水的密度一半大了一點點而已,連木材(700 kg/m3)都比不上!最悲劇的是進化之後連軟木塞的密度(240 kg/m3)都比牠們大。注意!我們這裡的單位是公斤/立方公尺(kg/m3),水的密度在這單位下是 1,000 kg/m3。

這該怎麼解釋呢?有幾個可能,一個是小拳石、隆隆岩牠們的表面是石頭構成的沒錯,但牠們骨子裡其實是由某種密度相當低的物質所組合的;二是圖鑑根本寫錯了。
我們先拿第一個假說來檢驗一下,並只以形狀最接近球形的隆隆岩作為範本。為了滿足體重 300 公斤的結果,貨真價實的岩石只能覆蓋隆隆岩全身 2 公分厚,而這一層石頭就重 250 公斤,剩下的 50 公斤則是留給半徑 0.68 公尺的球形身體。經過計算,這種情況下構成隆隆岩身體的物質密度為 37 公斤/立方公尺。
就連保麗龍的密度都有 70 公斤/立方公尺喔~ 這樣子在山上橫衝直撞真的好嗎?先別說薄的可憐、毫無岩石系寶可夢尊嚴的 2 公分厚岩石身體,只要隆隆岩稍微碰撞一下,體內器官不會就這麼碎一地嗎?只好打消 300 公斤的念頭、打臉這位記錄隆隆岩的博士,用紙筆重新判定隆隆岩的體重。
一樣拿隆隆岩為範例,既然身為一脈岩石系神奇寶貝的最終進化版,我想外皮至少有 20 公分厚的岩石應該算蠻合理的,而身體為剩下的半徑 50 公分圓球。這樣隆隆岩體內肌肉和岩石體積比例剛好差不多是 1:1,分別為 0.7 和 0.737 立方公尺,所以乘上密度、相加之後隆隆岩的理想體重應該要是 2553.56 公斤,他圖鑑體重的 8 倍多。(註2)
可以請這位負責的博士出面一下嗎?你的飯碗岌岌可危啊~

討論了一大堆之後,回歸到這次的主角隆隆岩,就算體重成謎,牠的圖鑑敘述中還是有幾個輕忽不得的點。(註3)
隆隆岩的豐功偉業之一是牠「能夠爆發出很強的能量,從這座山跳到另一座山」(銀、魂銀)
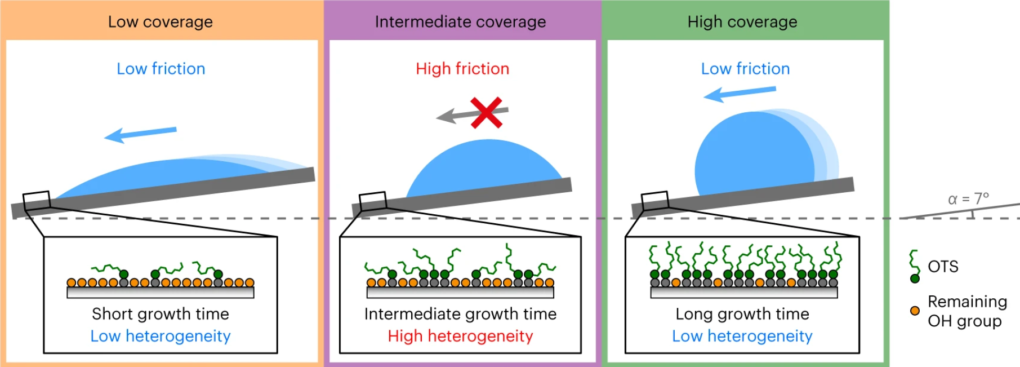
在不過度誇張的情況下,筆者從大屯火山群的地圖中找到了理想的地點:從七星山頂(1,120 公尺)飛越中湖戰備道路,跳到七股山頂(890 公尺),這兩座山頭只相差 1.2 公里,相對於從玉山跳到合歡山、從聖母峰跳到 k2 峰我想這是比較「合理」的情況了,所以這下子隆隆岩要怎麼跳呢?
根據拋物線運動公式,我們能夠得出如果隆隆岩要飛過這 1.2 公里的距離,牠必須以 108.4 m/s 的速度呈 45⁰ 起跳,整個過程費時 18.2 秒後,落在七股山頭,牠著地時時速為 127 m/s,釋放出 2,430,000 焦耳左右的能量。如果有一個不幸的傢伙剛好站在七股山頭看著冷水坑的美景,他會被相當於 2 輛 2 噸重的汽車以時速 115 公里同時撞上,或是 2 公斤的 TNT 炸藥爆炸的能量,而隆隆岩自己這樣還能毫髮無傷的話,那就表示牠是貨真價實的堅硬啊!(註4)
給大家參考一下,如果是你會挑哪兩座山?圖/陽明山國家公園 另一個隆隆岩的特性是牠 「時常從山上滾下來,留下一道深溝」(紅寶石、藍寶石、珍珠、終極紅寶石、始原藍寶石)
其實這是個一脈相傳的特性(註5),不管是小拳石還是隆隆石的圖鑑中都有如此記載,應該說從山上滾下來這件事對他們而言在正常不過,但牠們之中最重的隆隆岩從山上滾下來是會造成多大的影響呢?
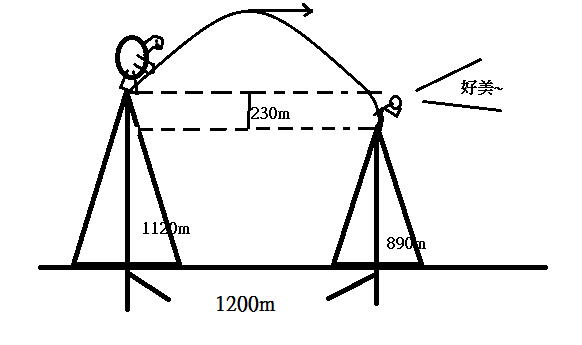
既然會危害到人類表示隆隆岩經過的地方應該是道路,所以首先我們得知道山坡段到底該有多陡。一段道路有多陡有個時常出現的說法為「坡度」,如果你是單車愛好者一定知道。「坡度」並不是指道路的角度,而是這段道路每前進 100 公尺會上升多少公尺,再換算成百分比,跟斜率相當類似。而從台灣交通部的資料中我們知道一旦道路的坡度 >7% ,就會設下警告標示,所以我們就當隆隆岩沿著坡度 7% 的道路滾下,在水平移動 100 公尺之後撞到某個不幸的路人。
經過計算之後,隆隆岩帶著 0.684 m/s2 的加速度衝下道路,當牠在 4.523 秒之後到達道路尾端時,時速為 11 公里,帶著總能量 55,350 焦耳,這能量差不多是高速公路上行駛的車子的一半,人直接被撞上大概會內傷吧….好消息是時速 11 公里跟腳踏車差不多,所以要閃開應該相當容易。
但別忘記這只是 7% 的路段,如果是新竹五指山的 17% 斜坡又另當別論了(註6)。如果隆隆岩從這裡滾下,在 100 公尺之後牠的時速會高達 85.5 公里,能量高達 334,400 焦耳,相當於被 3 輛 2 噸重的汽車以時速 115 公里同時撞上。

而且以上的狀況都是在只有一隻隆隆岩的情況下,如果加上牠的後輩們,成群的小拳石、隆隆岩一起沿著斜坡滾下來…….在寶可夢世界登山或騎單車真的是在玩命啊!真希望牠們的實際體重在少一點,一點點就好~
註解:
- 大家我沒忘記牠們都有手,隆隆岩甚至還有腳,小拳石更有跟自己臉一樣大的拳頭,但這樣只會徒增體積而已。
- 這裡我們假設構成隆隆岩身體的物質跟肌肉相似,也就是密度約等於水。經過一樣的計算之後隆隆岩的理想體重應該為 909 公斤,而最不球形的小拳石我沒有計算,但可能也是 8~9 倍,想像一下小剛把小拳石抱在手上…
- 除了以下會提到的幾點之外,8 成的隆隆岩介紹是 「每年會退一次皮,然後身體會迅速硬化」(黃、金、火紅、綠寶石、鑽石、心金、….等)、 「連炸藥都無法對牠造成損傷」(紅、藍、水晶、鑽石、葉綠、白金、鑽石….等),從這些介紹我們可以得知兩點:隆隆岩真的是生物;牠的皮應該不只是岩石,可能是更堅固的東西,但在更堅固只會讓牠的體重更不合理。
- 從註 3 我們提到了炸藥對隆隆岩一點用都沒有,所以這圖鑑敘述完全合乎常理,全寶可夢世界可能只有這傢伙能這樣玩了。
- 小拳石的介紹幾乎圍繞著牠「長得很像一般的石頭,登山客常踩到牠,小心牠會生氣」和「用粗壯的手臂爬到山頂」,至於爬到山頂幹嘛呢?我們從隆隆石的介紹知道了「時常從山上滾下來,路上壓過任何東西,停不下來」、「慢慢走回山頂,在滾下來」,還有最有趣的介紹是「牠一天能吃下 1 噸的石頭,尤其喜歡長滿苔蘚的」,從這個介紹我們知道牠們是貨真價實的動物,要吃下 1 噸的石頭大概是要過濾苔蘚吧~這樣根本多此一舉啊,直接肯苔蘚不就好了,幹嘛沒事吃比自己體重多那麼多倍的石頭啊~ 不會消化不良嗎?大便怎麼辦?
- R 編隊單車一竅不通,所以有任何讀者想要補充的嗎?似乎台灣還有 27% 的坡道,但那基本上少數人才會經過吧~
參考資料:
































-200x200.jpg)