大圈航法 (Great Circle Sailing)

• 撰文｜許世穎

「造父」是周穆王的專屬司機，也是現在「趙」姓的始祖。以它為名的「造父變星」則是標準燭光的一種，讓我們可以量測外星系的距離。這幫助哈柏發現了宇宙膨脹，大大開拓了人們對宇宙的視野。然而發現這件事情的天文學家勒梅特卻沒有獲得她該有的榮譽。

宇宙中的距離指引：標準燭光

經過了三篇文章的鋪陳以後，我們終於要離開銀河系，開始量測銀河系以外的星系距離。在前作＜天有多大？宇宙中的距離（3）—「人口普查」＞中，介紹了距離和亮度的關係。想像一支燃燒中、正在發光的蠟燭。距離愈遠，發出來的光照射到的範圍就愈大，看起來就會愈暗。

我們把「所有發射出來的光」稱為「光度」，而用「亮度」來描述實際上看到的亮暗程度，而它們之間的關係就是平方反比。一旦我們知道一支蠟燭的光度，再搭配我們看到的亮度，很自然地就可以推算出這支蠟燭所在區域的距離。

舉例來說，我們可以在台北望遠鏡觀測金門上的某支路燈亮度。如果能夠找到那支路燈的規格書，得知這支路燈的光度，就可以用亮度、光度來得到這支路燈的距離。如果英國倫敦也安裝了這支路燈，那我們也可以用一樣的方法來得知倫敦離我們有多遠。

我們把「知道光度的天體」稱為「標準燭光（Standard Candle）」。可是下一個問題馬上就來了：我們哪知道誰是標準燭光啊？經過許多的研究、推論、歸納、計算等方法，我們還是可以去「猜」出一些標準燭光的候選。接下來，我們就來實際認識一個最著名的標準燭光吧！

「造父」與「造父變星」

「造父」是中國的星官之一。傳說中，「造父」原本是五帝之一「顓頊」的後代。根據《史記‧本紀‧秦本紀》記載：造父很會駕車，因此當了西周天子周穆王的專屬司機。後來徐偃王叛亂，造父駕車載周穆王火速回城平亂。平亂後，周穆王把「趙城」（現在的中國山西省洪洞縣一帶）封給造父，而後造父就把他的姓氏就從本來的「嬴」改成了「趙」。因此，造父可是趙姓的始祖呢！（《史記‧本紀‧秦本紀》：造父以善御幸於周繆王……徐偃王作亂，造父為繆王御，長驅歸周，一日千里以救亂。繆王以趙城封造父，造父族由此為趙氏。）

回到星官「造父」上。造父是「北方七宿」中「危宿」的一員（圖一），位於西洋星座中的「仙王座（Cepheus）」。一共有五顆恆星（造父一到造父五），清代的星表《儀象考成》又加了另外五顆（造父增一到造父增五）。^[3]

英籍荷蘭裔天文學家約翰‧古德利克（John Goodricke，1764-1786）幼年因為發燒而失聰，也無法說話。1784 年古德利克（John Goodricke，1764-1786）發現「造父一」的光度會變化，代表它是一顆「變星（Variable）」。2 年後，年僅 22 歲的他就當選了英國皇家學會的會員。卻在 2 週後就就不幸因病去世。^[4]

造父一這顆變星的星等在 3.48 至 4.73 間週期性地變化，變化週期大約是 5.36 天（圖二）。經由後人持續的觀測，發現了更多不同的變星。其中一群變星的性質（週期、光譜類型、質量……等）與造父一接近，因此將這一類變星統稱為「造父變星（Cepheid Variable）」。^[5]

勒維特定律：週光關係

時間接著來到 1893 年，年僅 25 歲的亨麗埃塔‧勒維特（Henrietta Leavitt，1868-1921）她在哈佛大學天文台的工作。當時的哈佛天文台台長愛德華‧皮克林（Edward Pickering，1846-1919）為了減少人事開銷，將負責計算的男性職員換成了女性（當時的薪資只有男性的一半）。^[6]

這些「哈佛計算員（Harvard computers）」（圖三）的工作就是將已經拍攝好的感光板拿來分析、計算、紀錄等。這些計算員們在狹小的空間中分析龐大的天文數據，然而薪資卻比當時一般文書工作來的低。以勒維特來說，她的薪資是時薪 0.3 美元。順帶一提，這相當於現在時薪 9 美元左右，約略是台灣最低時薪的 1.5 倍。^[6][7][8]

勒維特接到的目標是「變星」，工作就是量測、記錄那些感光板上變星的亮度 。她在麥哲倫星雲中標示了上千個變星，包含了 47 顆造父變星。從這些造父變星的數據中她注意到：這些造父變星的亮度變化週期與它們的平均亮度有關！愈亮的造父變星，變化的週期就愈久。麥哲倫星雲離地球的距離並不遠，可以利用視差法量測出距離。用距離把亮度還原成光度以後，就能得到一個「光度與週期」的關係（圖四），稱為「週光關係（Period-luminosity relation）」，又稱為「勒維特定律（Leavitt’s Law）」。藉由週光關係，搭配觀測到的造父變星變化週期，就能得知它的平均光度，能把它當作一支標準燭光！^[6][8][10]

從「造父變星」與「宇宙膨脹」

發現造父變星的週光關係的數年後，埃德溫‧哈柏（Edwin Hubble，1889-1953）就在 M31 仙女座大星系中也發現了造父變星（圖五）。數個世紀以來，人們普遍認為 M31 只是銀河系中的一個天體。但在哈柏觀測造父變星之後才發現， M31 的距離遠遠遠遠超出銀河系的大小，最終確認了 M31 是一個獨立於銀河系之外的星系，也更進一步開拓了人類對宇宙尺度的想像。後來哈柏利用造父變星，得到了愈來愈多、愈來愈遠的星系距離。發現距離我們愈遠的星系，就以愈快的速度遠離我們。從中得到了「宇宙膨脹」的結論。^[10]

造父變星作為量測銀河系外星系距離的重要工具，然而勒維特卻沒有獲得該有的榮耀與待遇。當時的週光關係甚至是時任天文台的台長自己掛名發表的，而勒維特只作為一個「負責準備工作」的角色出現在該論文的第一句話。哈柏自己曾數度表示勒維特應受頒諾貝爾獎。1925 年，諾貝爾獎的評選委員之一打算將她列入提名，才得知勒維特已經因為癌症逝世了三年，由於諾貝爾獎原則上不會頒給逝世的學者，勒維特再也無法獲得這個該屬於她的殊榮。^[12]

本系列其它文章：

天有多大？宇宙中的距離（1）—從地球到太陽
天有多大？宇宙中的距離（2）—從太陽到鄰近恆星
天有多大？宇宙中的距離（3）—「人口普查」
天有多大？宇宙中的距離（4）—造父變星

—

參考資料：

[1] Astronomy / Meet Henrietta Leavitt, the woman who gave us a universal ruler
[2] wiki / 危宿敦煌星圖
[3] wiki / 造父 (星官)
[4] wiki / John Goodricke
[5] wiki / Classical Cepheid variable
[6] wiki / Henrietta Swan Leavitt
[7] Inflation Calculator
[8] aavso / Henrietta Leavitt – Celebrating the Forgotten Astronomer
[9] wiki / Harvard Computers
[10] wiki / Period-luminosity relation
[11] Universe Today / What are Cepheid Variables?
[12] Mile Markers to the Galaxies

• 撰文｜許世穎

本文轉載自 CASE 科學報 《天有多大？宇宙中的距離（2）—從太陽到鄰近恆星》

「視差（parallax）」是天文學家常用來量測距離的好工具。藉由視差，我們得以精準的量測地球到太陽的距離，再更進一步量測周遭恆星的距離。目前直接量測距離的方法中，視差是能量測最遠的一種，目前的極限大約是 1 萬光年。天文學家利用視差的概念已經很久了。然而在中古世紀，視差量測的結果卻讓當代的天文學家得出了「地球不會動」的結論……

太陽的距離：金星凌日、視差法

前作〈天有多大？宇宙中的距離（1）—從地球到太陽〉提到，我們可以在金星凌日的時候，藉由「視差（parallax）」來量測地球與金星的距離，並間接得到太陽的距離。「視差」就是「因為觀察位置不同，讓看到位置也不同」的現象。讀者們可以試試看，伸出一隻手指頭比個「1」、放在眼前大約 50 公分左右的地方。接著兩眼輪流交替閉上。如果讀者們真的有照做的話，應該會發現手指頭相較於背景來回大幅度地跳動。仔細觀察的話，會發現背景並不是不動，只是幅度很小而已。

從這個實驗我們得到幾個結論：（1）從不同的眼睛看出去，看到的物品位置會不同。這個現象就是視差；以及（2）距離愈近的東西，這個差異會愈大，也就是視差愈明顯（如圖 1）。我們可以根據這個視差的效果，來推算出物體的距離。

其實這也就是我們的眼睛判斷距離的方法！每個不同距離的物品從我們的左右眼看出去的位置差異不同。這兩個影像經過大腦判斷後，我們就可以得到距離的資訊。這也是 VR 實境立體畫面的原理。開發者先計算出每個物件在各自的距離下，兩眼會看到的視差效果。接著根據計算結果給予兩隻眼睛看到不一樣的畫面，我們的大腦就會自動合成出立體的圖像！

「兩個觀察位置的距離」稱為「基線（baseline）」，會影響視差的效果。一般而言，基線愈長，看到的視差就愈明顯。前面說到：「距離愈近的物品，視差會愈明顯。」換句話說，距離太遠的東西，視差就愈不容易觀察到。天文學家盡可能的把基線拉大，在兩個相距很遠的地方觀察天體，才能更精確的得到這些天體的距離。金星凌日發生的時候，科學家就是在地球找兩個相距很遠的地點做觀測，才有辦法測量出較為精確的金星視差，換算成金星的距離，最後計算出地球至太陽的距離。

鄰近恆星的距離：視差法……？

恆星當然也有視差了。提到量測恆星的視差，一定要提到 16 世紀著名的丹麥天文學家第谷．拉赫（Tycho Brahe）。當時還是個在爭論「地心說」、「日心說」的時代。他想利用恆星的時差來推論「地球到底會不會動」。如果「日心說」是對的，那麼隨著地球位置的不同，應該要看到恆星的視差。如果「地心說」才是對的，那麼因為地球的位置不變，不管怎麼觀察，恆星都不會出現視差。

在「日心說」的假設下，最遠的兩個觀察點是哪裡呢？可不是地球的兩端，而是「相隔 6 個月的地球」！可以想像，如果地球繞著太陽每一年繞轉一圈的話，那麼相隔 6 個月的地球會在太陽的兩端，這個間距可比地球的兩端大多了（見圖 2）！既然兩個觀測點是地球在太陽兩端，就代表基線（兩個觀測點間距）就是 2 倍的「日-地距（地球到太陽距離）」。用前面的方法得到的「日-地距」愈精確，那麼藉由視差法測出來到恆星的距離就能愈準。

為了精密的量測恆星的位置，必須要有非常良好的天文台。第谷可是丹麥的貴族啊！他直接花錢蓋了一棟天文台來量測、紀錄星星的位置，卻發現怎麼樣都量測不出恆星的視差。這代表了兩個可能性，一個是「地球不動」，另一個可能性就是「恆星太遠」。第谷認為，如果恆星真的這麼遠，而我們在地球上還是看得到的話，這些恆星未免太大了！他認為這不太可能，因此認定「地球不動」。

那到底哪裡出錯了呢？用一個簡單的例子來說明：「拿捲尺去量一張紙的厚度，當然怎麼量厚度都是 0 公分啊！」其實第谷的推論完全合理，量測不到恆星視差的原因真的就是因為「恆星太遠」，所以視差太小而無法看到。從現代的數據我們可以回推他當時的情況，太陽以外最近的一顆恆星是位於「半人馬座」裡的「比鄰星（Proxima Centauri）」，距離是 4.22 光年。產生的視差比第谷使用的天文台精密度還要更小了好幾倍！他所推估這些恆星的大小從現在眼光來看也非不合理，只是真的難以想像。

現在的我們有了更良好的儀器，已經可以靠視差來推算恆星的距離了。不過視差法曠日費時，倒也不難理解，畢竟要有好的基線要等半年啊……而且儀器的辨識率也是有極限的，目前視差法的極限差不多是 10 微角秒（1 角秒為 1/360 度） ^[2]，相當於十億分之一度！換算成能量測到的距離極限，差不多是 1 萬 6 千光年左右。聽起來很多嗎？銀河系的直徑約 10 萬至 18 萬光年，這個距離極限連銀河系都看不穿。所以視差法雖然好用，但只能拿來測量鄰近恆星的距離（見圖 3）。

視差法是直接量測距離的盡頭了。想要把銀河系看穿、想要知道銀河系中其他成員們的距離，我們得開始「間接量測」。先做出一些物理學上的假設，才能夠「猜」出距離。想要知道更遙遠的距離，則需要更多的假設，這個概念叫做「宇宙距離階梯（cosmic distance ladder）」。下一篇文章中，我們將帶大家進行恆星的「人口普查」，並且利用普查結果來得到更遙遠的距離。

參考資料

1. pixabay / martinklass
2. wiki / Parallax
3. 網路天文館 / 恆星的距離測量

本系列其它文章
天有多大？宇宙中的距離（1）—從地球到太陽
天有多大？宇宙中的距離（2）—從太陽到鄰近恆星
天有多大？宇宙中的距離（3）—「人口普查」

• 文／雞湯來了蕭子喬
• 校稿／雞湯來了陳世芃、張芷晴
• 製圖／雞湯來了黃珮甄
• 編輯／雞湯來了蕭子喬

防疫期間，家中有人改為線上上課，也不能出去趴趴走放電；有人改為在家上班，時不時忙於搶口罩、酒精……人心惶惶，許多人都受疫情、作息變動而苦。躁動不安的物種長時間相處在一起，該如何保持心理的相互支持、不吵架和平相處？

本文使用「親子界線」理論觀點，帶你看家人之間「心」的社交距離，多遠才恰恰好？

貼心提醒：依據所參考的研究資料，本文中親子以大學生及其家長為主要情境。

如果你是大學生以上，可以試想自己是測驗中的主角；

如果你是大學生以上的家長，可以試想自己平時如何與孩子互動的？他感受為何？

如果你是家有青少年以下的家長，可以試想自己從現在開始累積的教養方式，可以如何營造更融洽的親子關係？

測驗我的家人關係－「親子界限」觀點

防疫期間，許多人都說社交距離要保持 1.5 公尺，但心要很靠近！

然而，對於朝夕相處的家人來說，心的距離如何才「剛剛好」可能有不同的邏輯。

由於幾乎整天都待在同一時空，時常能相互關心，但摩擦干擾也可能隨之增加。因此，親子之間的社交距離重點應放在如何「不太近也不太遠」，拿捏在一個能夠相互支持，但不致過度糾結干擾的狀態。

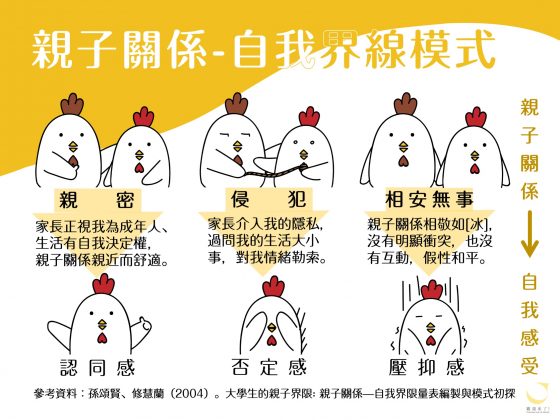
台灣學者以西方學者 (Green&Werner) 提出的家人界限理論概念為基礎，嘗試加入本土親子相處特性，訪談近 70 位 20 多歲的成年人和家人的相處狀況，歸納出台灣的親子關係常見具有「親密」、「侵犯」及「相安無事」三種類型，分別反映著「認同」、「否定」及「壓抑」三種自我感受。

同時看見關係的狀態，及對個人心理感受的影響，才能充分找到平衡的出路。

點我測驗！

親子親密－認同感

親密的親子關係長什麼樣子呢？有的是父母提供孩子經濟、生活上的照顧，相互陪伴、一起參與活動，親子之間時常主動分享生活瑣事、對事情的看法，也充分表達彼此的情感，例如擁抱、說出支持、也能撒嬌等。

也有的是家中形成三角同盟的現象，例如某人拉某人成為同一國，一同說服、反對另一個家人，此時同一國者會形成親密感，不過此狀態對於整體家人之間的和諧，以及孩子的身心發展可能有不良影響。

延伸閱讀：當孩子成為大人拉鋸戰的爭奪品，親職化孩子的心境

值得注意的是，親密感並不一定需要彼此緊密的連結，許多受訪者提到，若能給予彼此空間發展自我，反而會讓彼此的關係感到親近。

在上述親密的關係下，個體會經驗到被認同、有自主性，與家長平等的感受，家長正視孩子已是一個成年人而非小孩，會讓孩子感到親子之間是親近的，且對於自己生活有決定權，不會受到太多干涉或操控。

親子侵犯－否定感

家長侵犯孩子自主空間的關係主要來自於「實體空間」及「心靈空間」的侵犯，如家長隨意觀看孩子的隱私、進入孩子個人空間、凡事都要問、甚至對孩子的生活多有指責，或是常見的「情緒勒索」，孩子受到家長情緒的干擾，甚至家長情緒化的語言或行為成為綁住孩子的工具。

在上述受到侵犯的關係下，孩子會經驗到被否定的感受，認為自主權被剝奪，自己的表現被質疑。該研究還特別強調，尤其是在生涯發展方面，若父母對孩子多干涉甚至操作，會使孩子強烈感受到父母與自己理念相距甚遠，且感受到被侵犯及否定。

親子相安－壓抑感

這裡的相安，指的是表面相安無事，但心裡缺乏連結的狀態，有可能話題缺乏深度和廣度，雖有交談卻感無味，例如總是在談學業、成就。也有的是彼此維持著表面的和諧，及始終不說的秘密，維持著一種假笑般的安全關係。

還有的孩子感受到家長需要權威和決定權，但孩子也想保有自主決定權，此時孩子為了使關係保持和諧，並做出妥協，給予家長某部分的決定權。

親子相安的類型，有點類似相敬如「冰」的概念，看起來沒有明顯衝突，但其實是虛假的和諧。此類型家長較少給予鼓勵或正向回饋，較多責備與要求，孩子會感受到溝通時曖昧不清，以為對方理解其實缺乏深入內心想法的溝通，長期下來會經驗到疏離與壓抑感。

相關推薦：《你的孩子不是你的孩子》剖析失衡的親子關係的原因

看到這裡，你覺得你比較像哪類型呢？

其實，親子關係是從出生到老都伴隨著我們的，有相愛相殺的時刻，也有真心相擁的溫暖懷抱，一時說不清也是很正常的。讓我們一起試著從自身感受出發，藉由上方測驗，釐清親子關係對於自己的意義與影響是什麼，進而找出更舒適的狀態。

如果你主要類型是親密－認同感，那恭喜你，你有著舒適的親子關係，如果你主要感受到的是侵犯－否定感、相安疏離－壓抑感，那麼可以試著藉由有效溝通的方法，向家人表達我們的感受。

相關推薦：我們的關係，還有沒有救？扭轉僵化習慣的方法

相關推薦：「我訊息」‌溫和而堅定表達出自己想法

親子剛剛好的距離：不疏離也不太黏的 5 個具體作法

防疫期間親子長期待在同一個時空，心情和作息都會互相影響，壓抑或否定感都可能快速累積爆棚，親密感也有可能短時間內感覺變成太黏。

讓我們試著藉由以下 5 種方法，找到和家人適當的距離，不疏離也不太黏！

1. 空間：

   為家裡的空間重新定義！例如某房間，或小至一張桌子、客廳的某個角落就是臨時辦公室／教室，並盡可能把大人和孩子工作／上課的空間拉開距離。雖然長時間待在家，但還是要為每一個家人盡可能打造獨立屬於自己的空間。

2. 時間：
   

   在家也有上下班、上下課時間！即使整天在家，還是需要劃分固定時段上課或上班，並建立時空切換的儀式感，應盡可能避免全家人的作息和聲音過度交織在一起，可以是共同討論哪些時段各自做事，盡量互不干擾。
   重新擬定全家新作息-３個具體做法成為時間的好主人

3. 心態：

   建立角色切換的心態，例如白天我是「上班族／公司員工／大學生」，傍晚後是「家中成員，例如媽媽／女兒」等，也可以利用服裝的切換，增加儀式感，使自己即使整天在家也能有效在對的時間建立對的心態。
   「家事」是「我們家」的事！— 3 步驟重新調配家事分工
   特殊時期，如何當個教養神隊友？

4. 心情：

   在防疫期間，許多人心情都會變得較為緊繃，不過家中的每一個人都牽動著其他人的心情波動。因此，我們可以試著在網路或書中找一些紓壓的方法，緩解焦慮的心情，例如播放紓壓靜心的音樂，讓心情處在較為平和的狀態。也可以從自己開始示範，面對壓力的紓壓自處之道，為家人建立良好模範。
   「你累了嗎？」當工作壓力悄悄地被帶回家…家庭壓力理論告訴我們的新出路
   我家有刺蝟！好難溝通怎麼辦？—薩提爾的情緒覺察練習
   沒有「壞」情緒！接受孩子的當下反應 －3 步驟，打開孩子的心門

5. 把話好好說：

   即使煩躁，會覺得家人干擾到自己的時間／空間，還是要留心自己的用語，用平和的方式說出自己真實感受，家人多半較能理解，避免用攻擊性字眼、指責性語氣，挑起對方戰鬥或逃跑的心態，造成更多的爭吵或煩悶。
   雙贏溝通（上）「三明治說話術」把話好好說，對方順耳聽
   雙‌贏‌溝‌通‌（下）‌「我訊息」‌溫和而堅定表達出自己想法

還記得本文一開始的親子關係距離圖嗎？其實並沒有哪個類型才是「好」的，只有哪個狀態對你和家人而言是共同最「舒適」的。

可以先想想你現在是哪種狀態？再想想你希望的是哪種狀態？如果之間沒有落差，那麼可以想想如何保持這樣理想狀態？如果有落差，那麼可以想想如何調整，重新為彼此的關係互動模式定調？

在防疫特殊期間，用上述 5 個方法，盡可能從容自處、自在相處！

參考資料

1. 孫頌賢、修慧蘭 (2004)。大學生的親子界限∶ 親子關係—自我界限量表編製與模式初探。測驗學刊，51 (1)，45-78。
2. 修慧蘭 (2011)。何謂糾結／疏離關係－本土大學生親子界限之研究。諮商輔導學報：高師輔導所刊，23，1-18。
3. 張在蓓、張世華 (2019)。青少年母親親職適應團體之成效研究－Bowen 家庭系統理論之運用。中華輔導與諮商學報，56，59-95。

本文與雞湯來了同步刊登：防疫待在家系列：親子「心」距離不疏離不太黏的 5 個做法