- 撰文|許世穎
本文轉載自 CASE 科學報 《天有多大?天文學中的距離(1)—從地球到太陽》
天文學中要怎麼量測長度或距離呢?地球上常用的直尺、捲尺、雷射測距儀等恐怕不是那麼適合。比較近的天體還有辦法直接量測,遠距離的只好仰賴一些間接的推斷。我們先從古埃及利用井、尖塔、駱駝推算出地球的周長出發,進而介紹利用雷達天文學等方法量測太陽系中月球、行星距離的方法。
地球周長:井、尖塔、駱駝
平常我們怎麼量測長度或距離呢?如果是桌上的小東西,我們可以用直尺;如果稍微遠一些,可以利用捲尺;再更遠一點的話可以利用雷射測距儀。這些都是地球上常見、常使用的距離量測工具。那當距離更遠的時候要怎麼辦呢?我們該怎麼量測地球的周長呢?月球、太陽有多遠呢?更遙遠的天體該怎麼辦呢?
我們不能一步登天。要先從比較近的開始直接量測,接著再想辦法間接推敲出遙遠天體的距離。就讓我們先從最近的「地球周長」開始吧!其實早在古希臘,畢達哥拉斯就已經提出了地球是「球」的想法。埃及學者埃拉托斯特尼(Eratosthenes)在公元前 240 年,就估計出一個地球周長的數值。這個算法很有趣,讓我們搭配圖 1 一起來看看。
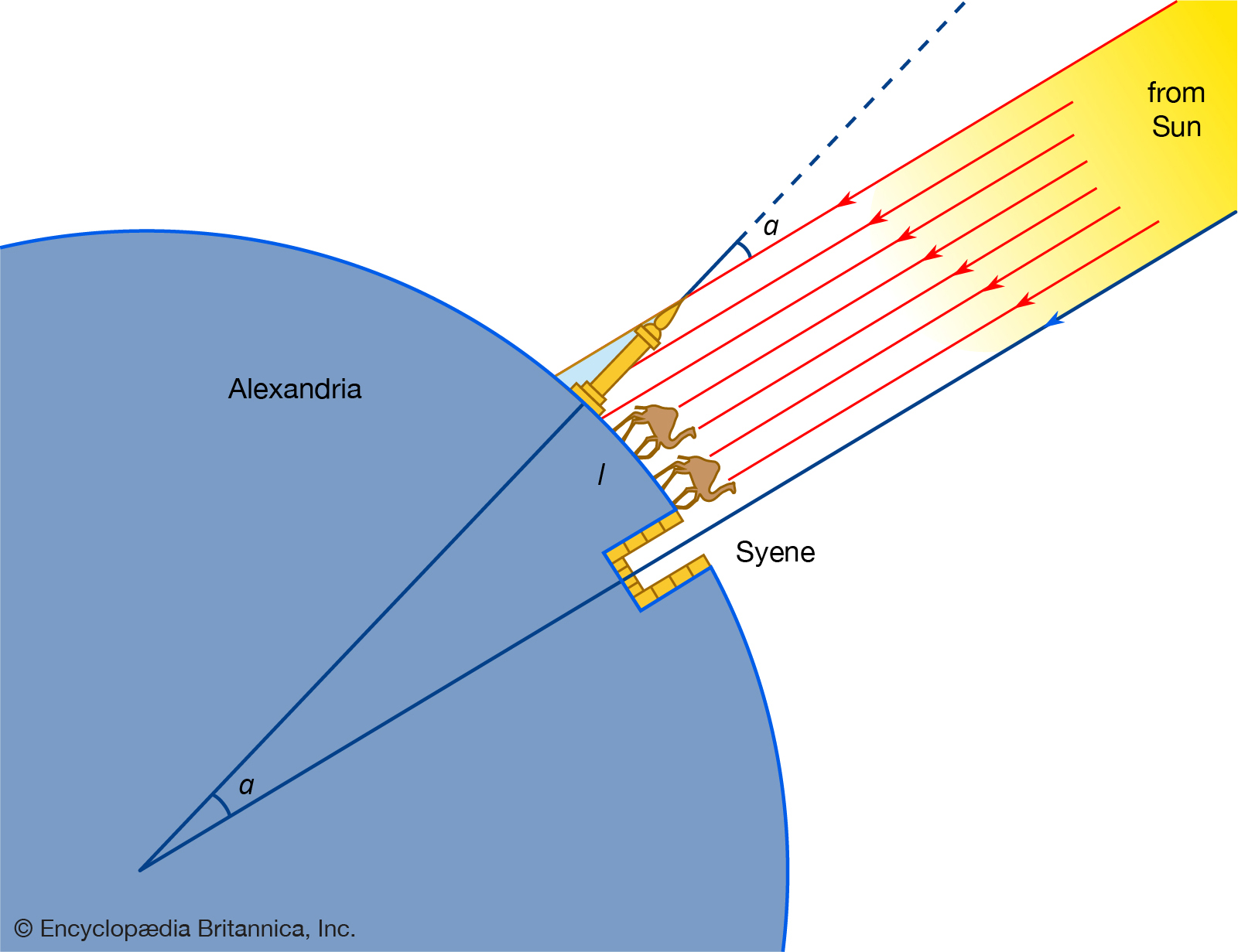
首先,他知道在夏至那天,可以從埃及城市「賽伊尼(Syene,即現在的Aswan)」的一座井中,看到太陽從正上方來的倒影。也就是說,夏至這一天太陽光會剛好直曬賽伊尼。他進一步量測,在夏至這一天,亞歷山大城(Alexandria)方尖石塔的影子長度。從這個影子長度和方尖石塔的高度,可以計算出太陽的天頂角 α。而因為三角形相似形的關係,這個天頂角 α 同時也會是賽伊尼與亞歷山大城在地球上的夾角。這個天頂角 α 約為 7.2°,因為7.2°佔了整個圓 360° 的 50 分之 1,所以將距離乘以 50,就是地球的圓周長。
也就是說,只要找到賽伊尼與亞歷山大城之間的距離,再乘上 50,就是地球的圓周長…但是兩座城市之間的距離要怎麼知道呢?他從商隊那裏問到,這兩座城市要讓駱駝走 50 天,在經過一些計算即換算後,他得到地球的圓周長大約是 252000「stadia」(當時埃及的距離單位)。雖然他所用的單位「stadia」與現代長度單位的換算已經無法考證,但現代科學家認為他所量測出的這個數字約為 39,690 公里到 46,620 公里之間,與現代的公認值差異只有 1%-15% 左右而已![3]
月球距離:月食、雷射、反射鏡
有了地球的大小以後,再來讓我們來量月球吧!先從量測月球地球距離開始,其中一個方法是利用「月食」。這個方法可以追溯至希臘天文學家阿里斯塔克斯(Aristarkhos,310-230 B.C.)。他其實是紀載中最早提出日心說的人,可惜並沒有受到非常廣泛的認可。月食就是月亮進入了地球的影子。將地球影子的大小除上月食發生的時間就是月球移動的速度。而將月球移動的速度乘上月球繞一圈的時間(28 天左右),就可以得到月球繞地球的圓周長、半徑。
較為現代、更為直接的方法就是「雷射測距」,原理就跟雷射測距儀差不多。從地球上發射雷射光到月球上,藉由量測反射光,可以知道光來回所需要的時間,再乘上光速,就可以得到月球的距離囉。這個時間約為 2.5 秒,換算後的月地距離約為 38 萬公里。

為了擁有更好的雷射光反射效果,人類還在月球上擺放了 5 個反射器,分別在 5 次人類登陸月球的任務中放置(3 次美國、2 次蘇聯,見圖 2)。這些反射器讓月地距離的精密度提升到了毫米等級。美國著名生活喜劇影集《The Big Bang Theory》裡面就有進行這個實驗的片段,讀者不妨去看看:Learn English with The Big Bang Theory: Blowing up the Moon(有字幕、英文教學版本)。
精確的月地距離量測也帶給我們有趣的發現。比方說發現或量測出:月球每年以 3.8 公分的速率離地球愈來愈遠;月球內部可能有著月球半徑 5 分之 1 大小的液態核心;月球除了原先的運動以外,還有著額外的晃動,稱為「天平動(libration)」…等 [5]。
行星距離:雷達
量測行星距離的方法類似量測月球距離的方法,只是行星的距離通常太過遙遠,使用一般的雷射光的話效果不好,必須改使用微波的波段,這個學門稱為「雷達天文學(radar astronomy)」。雷達天文學所使用的設備必須要能夠向宇宙發射高功率的微波,過去常用的天文台包含「阿雷西博天文台」(Arecibo Observatory)與「戈德斯通天文台(Goldstone Observatory,見圖 3)」
(延伸閱讀:再見了:阿雷西博天文台!)

雷達天文學被運用太陽系內天體的研究,畢竟再更遠的話反射的訊號會太弱。在過去,雷達天文學除了幫助我們量測行星的距離,還可以拿來觀測天體的表面狀況 [7]。
太陽的距離:金星凌日
地球與太陽的平均距離稱為 1 個「天文單位(Astronomical Unit,簡稱 AU 或 au)」。要量測日地距離的話,總沒辦法用雷射測距了,太陽自己的光線太強、也沒辦法反射雷射光或微波,更不可能讓人上去裝設反射鏡。那該怎麼辦呢?我們可以利用「金星凌日」來幫忙!

金星凌日是指從地球上看出去,金星從太陽前面經過的現象(圖 4)」。而這也是太陽、金星、地球接近一直線的時候。就好像是我們用手遮住陽光時,太陽、手、我們的眼睛會排列成一直線一樣。
根據克卜勒定律,我們可以計算出金星的軌道半徑為 0.72 天文單位。地球軌道半徑則是 1 天文單位。當太陽、金星、地球排成一直線時,可以得到金星與地球的距離是 0.28 天文單位。這時候只要量測出金星的距離,就可以換算出 1 天文單位的大小!
然而這個狀態下,在金星後面的太陽會嚴重干擾訊號,因此無法使用雷達來量測金星的距離。得靠別的方法來找出距離,這個方法稱為「視差(parallax)」。至於視差要怎麼使用,又怎麼讓丹麥天文學家、第谷使用正確的數據、正確的儀器、正確的推論、得到完全錯誤的結果,則是另一段故事了。
(待續)
參考資料
- Free Images / Bedouin watching a caravan passing by near the pyramids of Giza
- Eratosthenes | Biography, Discoveries, Sieve, & Facts | Britannica
- wiki / Eratosthenes
- The New York Times / How Do You Solve a Moon Mystery? Fire a Laser at It
- wiki / Lunar Laser Ranging experiment
- wiki / Goldstone Deep Space Communications Complex
- wiki / Radar astronomy
- SPACE / Venus Crosses the Sun for Last Time Until 2117, Skywatchers Rejoice
本系列其它文章
天有多大?宇宙中的距離(1)—從地球到太陽
天有多大?宇宙中的距離(2)—從太陽到鄰近恆星
天有多大?宇宙中的距離(3)—「人口普查」
天有多大?宇宙中的距離(4)—造父變星